Blog

We just published a new paper in the Journal of Vision

The temporal dynamics of eye movements as an exploitation-exploration dilemma
Ehinger Kaufhold & König, 2018

The highlights:

• We put eye movements as a decision process between exploitating the current view and exploring more of the scene
• We use gaze-contingent eye-tracking to control the When and Where of eye movements
• We find large effects of how long a subject fixates on their reaction time to continue exploring
• We find large effects of the number of possible future target locations (Hick’s effect)

Check out the paper at the Journal of Vision
doi:10.1167/18.3.6

Often when developing with psychotoolbox or psychopy/opensesame your program crashes. And I often then have a full-screen window open and cannot click somewhere else. I then try to Alt+Tab and execute “sca” (screen close all) into the matlab console, with often mixed success. Sometimes restarting the computer is the last option. Instead of restarting, a useful command in older ubuntu versions was: STRG + ALT + Backspace => restart X server (=> restart GUI).

In order to activate this again use:

setxkbmap -option terminate:ctrl_alt_bksp

source on askubuntu

PS: I wrote this blogpost because I looked up this thing multiple times – now I know where to look 😉

From time to time I explain concepts and ideas to my students.

Background

Often this pops up in a statistical context, when one has a non-linear dependency between the to-be-predicted variable and the predictor-variables. By transforming the predictors, relationships can be made linear, i.e. a logarithmic (exponential, quadratic etc.) relationships can be modeled by a **linear** model.

The idea

I have a very visual understanding on basis-functions / non-linear transformation of variables in terms of stretching / condensing the basis (the x-axis here). This can also be applied to the generalized linear model (here for logistic regression).

Imagine that the x-axis of a plot is made of some kind of elastic material, you can stretch and condense it. Of course you do not need to stretch every part equally, one example would be to stretch parts that are far away from zero, exponentially more than parts that are close to zero. If you would have an exponential relationship ($ y = e^x$) then $y$ would now lie on a straight line.

TLDR;

Imagine you have a non-linear relationship, by stretching the x-axis in accordance to that non-linear relationship, you will have a linear relationship.

An exemplary non-linear relationship:

We want to do $y = b_0 + b_1x $ but obviously a linear line does not fit well. We can do something called polynomial expansion, i.e. add more predictors which are simple transformations of the predictor $x$. i.e. $y = b_0 + b_1x + b_2x^2 + b_3x^3$

The trick comes here: We can interpret the new $x^3$ basis function as a stretching of the x-axis. I.e. the further we move out on the x-axis, the longer we need to stretch the parts (exactly by x^3 times)

This can be shown also for other functions:

Exponential

Logarithmic

Note that the logarithm is not defined for negative numbers

Quadratic

Note how the stretching can be negative, i.e. the original negative values are stretching/transformed to positive values

Using the trick on the y-axis

One can interprete **logistic regression** with the same trick:
$$ g{-1}(y) = b_0 + b_1*x <=> y = g(b_0+b_1x)$$
with $g$, the logistic (logit) function and $g^{-1}$ the inverse logistic function (invlogit)
$$ g^{-1} = \ln\frac{p}{1-p} <=> g = \frac{1}{1+e^{-x}}$$

Usually we would have some non-linear dependency on a probabilty of e.g. success. That means, with a low value of x, your success-chance are low. To model this kind of data, one can transform the y-axis using $g$ above.

Sometimes I need matlab/rstudio/spyder but with access to the university network. One way is to run matlab/rstudio/spyder on the university computers, but get the X (=Graphics) display on my local windows machine.

Because there is a gateway in between, I first need to tunnel the gateway to a university working computer, then use a second putty session to ssh right through the tunnel directly to the target computer.

These are the steps I need to do:

– Putty: ssh to gateway.university:22;  Go to SSH-Tunnel and put source-port: 2222 (this is your local port you gonna target the second session). destination: remote-pc-that-runs-matlab:22

– Putty again: ssh to localhost:2222 with X11 forward enabled and “xming” installed

and perfect (but sometimes slow) remote-X11-forwarding. For the future I want to check out rdb to remotely control the session. This could be a quite useful in many cases because my programs are usually running anyway 🙂

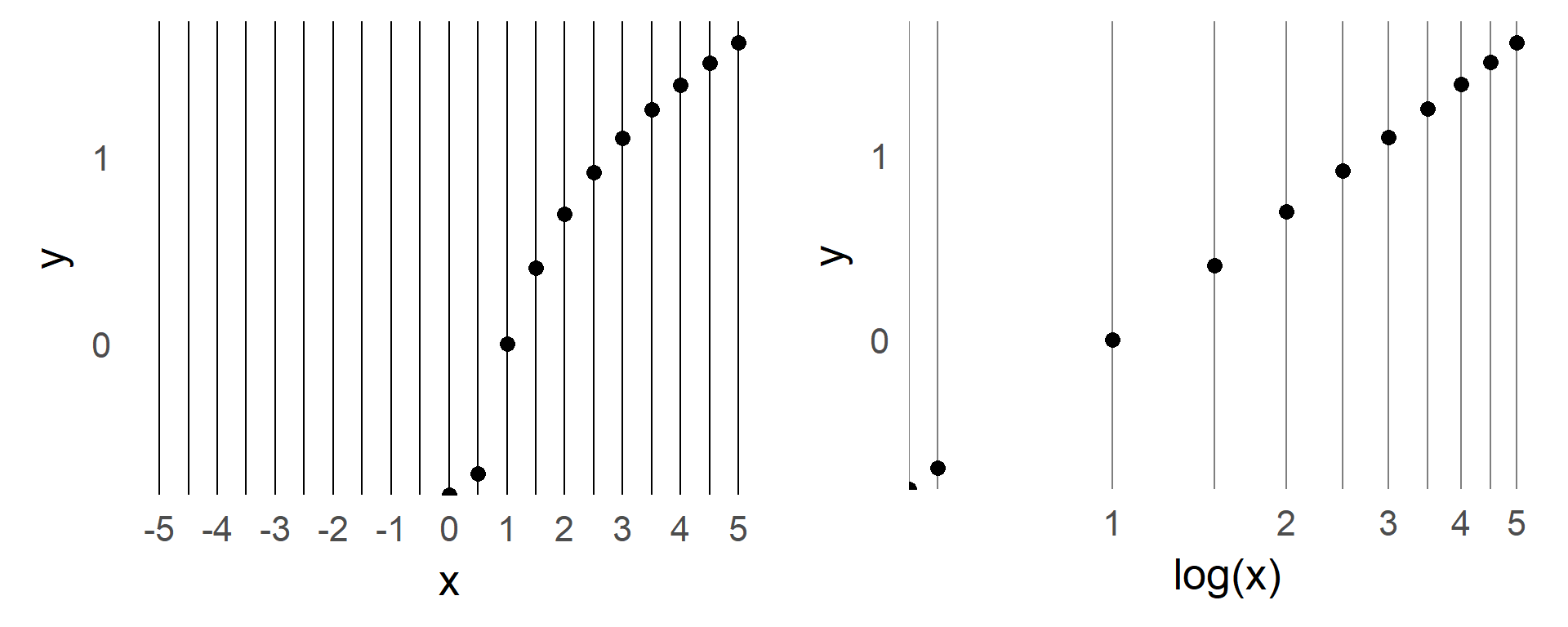
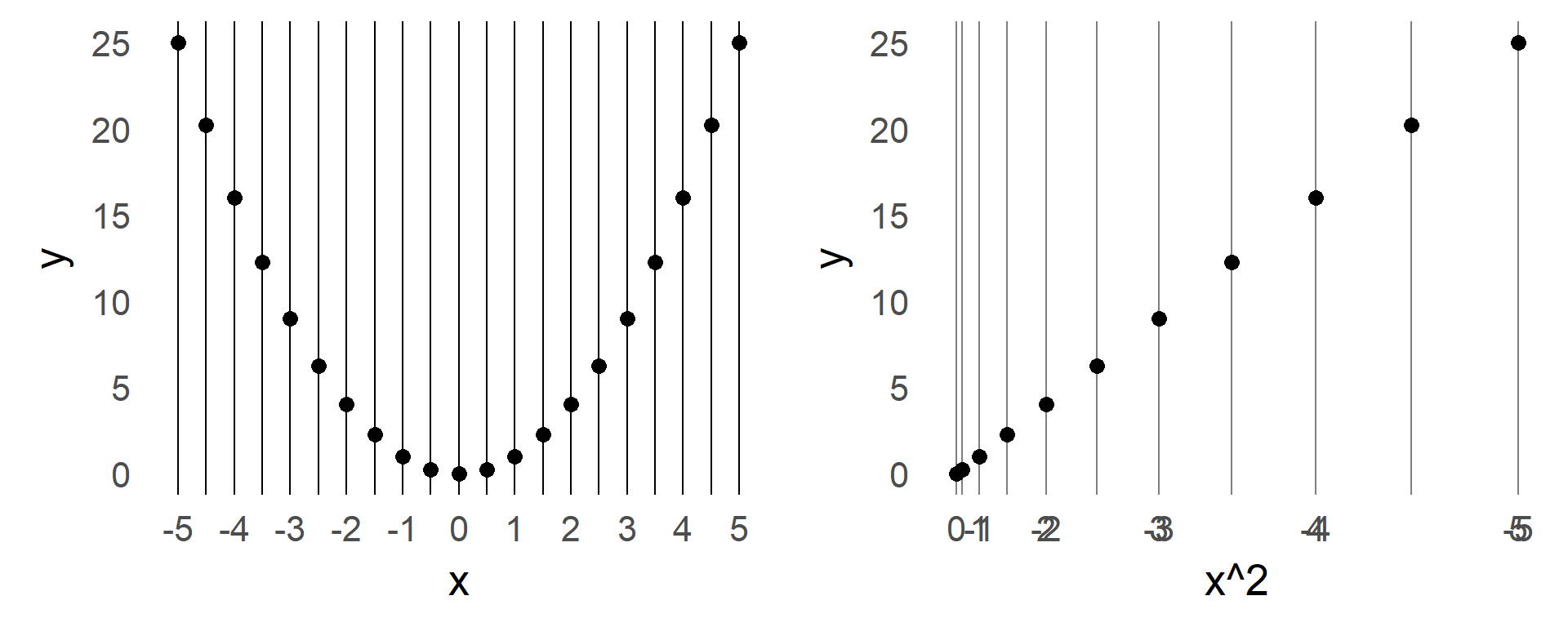
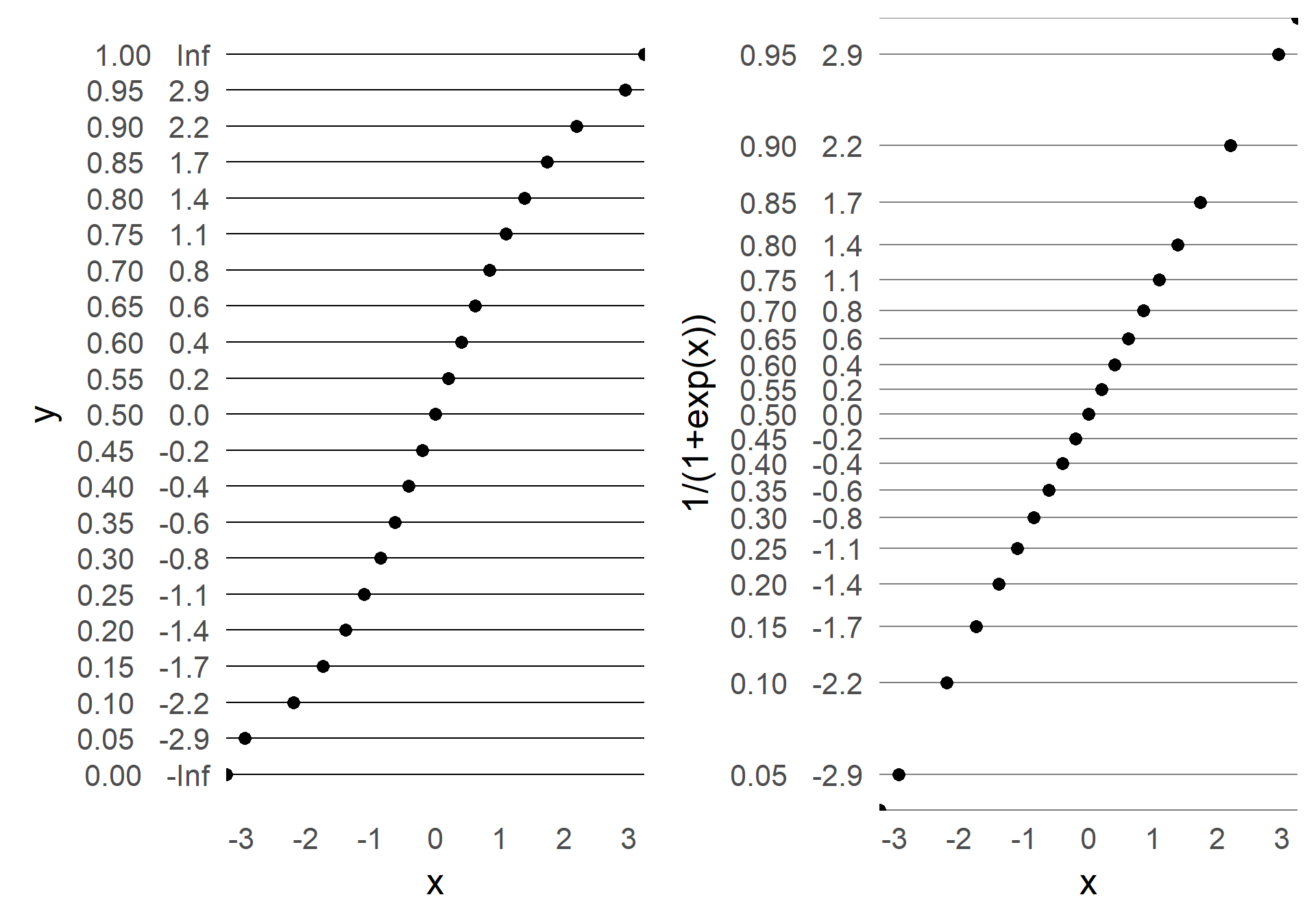
From time to time I explain my students certain concepts. To archive those and as an extended memory, I share them here. We also recently had some discussion on vectorization in our research group. e.g. in python and matlab. With the second link claiming for-loops in matlab are performing much better than before.

Goal

Show that for-loops are still quite slow in matlab. Compare bsxfun against vectorized arithmetic expansion in matlab against bsxfun

The contenders

• good old for-loop: Easy to understand, can be found everywhere, slow
• arithmetic expansion: medium difficulty, should be general used, fast
• bsxfun: somewhat difficult to understand, I use it regularily, fast (often)

Comparisons

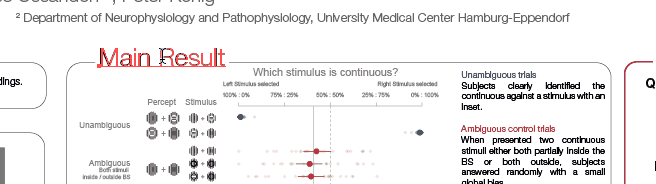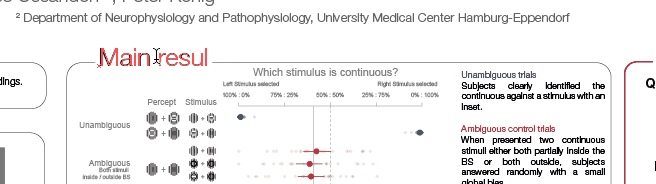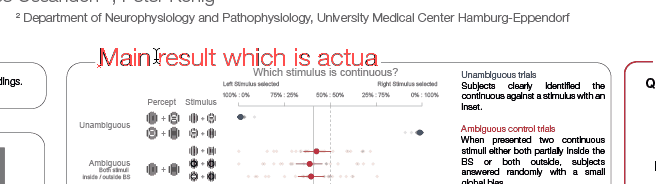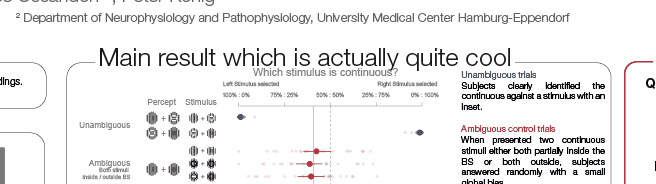
While demonstrating this to my student, I noticed that subsetting an array has interesting effects on the performance differences. The same is true for different array sizes. Therefore, I decided to systematically compare those.

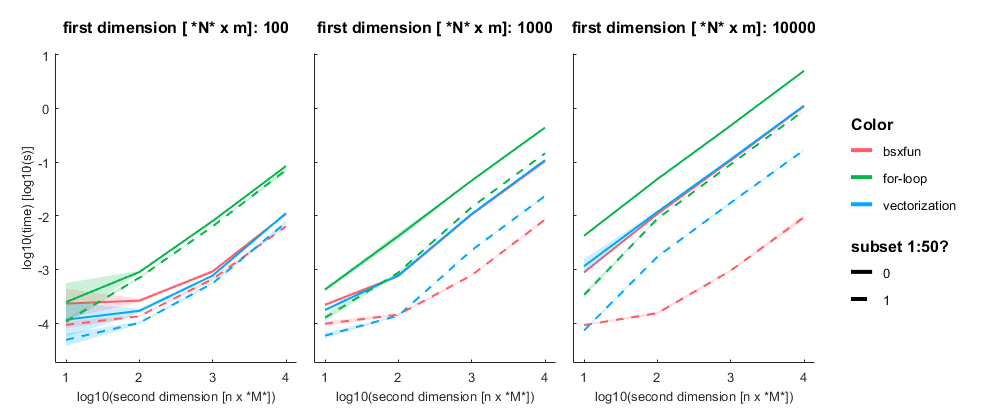
I subtract one row from either a subset (first 50 rows, dashed line) or all rows of an [n x m] matrix with n= [100, 1000, 10 000] and m = [10, 100, 1000, 10 000]. Mean + SE

Three take home messages:

• for loop is very slow
• vectorization is fastest for small first dimension, then equally fast as bsxfun
• bsxfun is fastest if one needs to subset a medium sized array (n x m >100 x 1000), but see update below!

Update:

Prompted by Anne Urai, I redid the analysis with multiplication & devision. The pattern is the same. I did notice that allocating new matrices before doing the arithmetic expansion (vectorization) results in the same behaviour as bsxfun (but more lines of code)

A = data(ix,:);
B = data(1,:);
x = A./B;

matlab code

tAll = [];
for dim1 = [100 1000 10000]
    for dim2 = [10 100 1000 10000]
        tStart = tic;
        for subset = [0 1]
            if subset
                ix = 1:50;
            else
                ix = 1:dim1;
            end
            for run = 1:10
                data = rand(dim1,dim2);
                
                % for-loop
                x = data;
                tic
                for k= 1:size(data,2)
                    x(ix,k) = data(ix,k)-data(1,k);
                end
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'for-loop'},t)];
                %vectorized
                tic
                x = data(ix,:)-data(1,:);
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'vectorization'},t)];
                % bsxfun
                
                tic
                x= bsxfun(@minus,data(ix,:),data(1,:));
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'bsxfun'},t)];  
            end
        end
        fprintf('finished dim1=%i,dim2=%i - took me %.2fs\n',dim1,dim2,toc(tStart))
    end
end

% Plotting using the awesome GRAMM-toolbox
% https://github.com/piermorel/gramm
figure
g = gramm('x',log10(tAll.dim2),'y',log10(tAll.t),'color',tAll.Var4,'linestyle',tAll.subset);
g.facet_grid([],tAll.dim1)
g.stat_summary()
g.set_names('x','log10(second dimension [n x *M*])','y','log10(time) [log10(s)]','column','first dimension [ *N* x m]','linestyle','subset 1:50?')
g.draw()

I got asked for the design of my academic posters. Indeed I have templates in landscape and portrait and I’m happy to share them. In addition I can recommend the blog better-posters which has regularily features and link-roundups on poster-design related things.

In my newest poster (landscape below) I tried to move as much text to the side, so that people can still understand the poster, but it does not obscure the content. I also really like the 15s summary, an easy way to see whether you will like the poster, or you can simply move on. Maybe it even needs to be a 5s summary!

These are two examples posters based on my template.

Neat Features

Titles’ backgrounds follow along

This is useful because you do not manually need to resize the white background of the text that overlays on the borders

Borders are effects, easy resizing

The corners are based on illustrator effects, thus resizing the containers does not change the curvature. Before I often had very strange curvatures in my boxes. No more!

Download here

Portrait Equal Columns (ai-template, 0.3mb)

Portrait Unequal Columns (ai-template, 0.3mb)

Landscape (ai-template, 0.4mb)

Licence is CC-4.0, you can aknowledge me if you want, but no need if you don’t 🙂

We recently published an article (free to read): “Humans treat unreliable filled-in percepts as more real than veridical ones”. Inspired by Selim Onat and many others, I try to to explain the main findings in plain language. First let me give you some background:

To make sense of the world around us, we must combine information from multiple sources while taking into account how reliable they are. When crossing the street, for example, we usually rely more on input from our eyes than our ears. However we can reassess our reliability estimate: on a foggy day with poor visibility, we might prioritize listening for traffic instead.

The human blind spots

But how do we assess the reliability of information generated within the brain itself? We are able to see because the brain constructs an image based on the patterns of activity of light-sensitive proteins in a part of the eye called the retina. However, there is a point on the retina where the presence of the optic nerve leaves no space for light-sensitive receptors. This means there is a corresponding point in our visual field where the brain receives no visual input from the outside world. To prevent us from perceiving this gap, known as the visual blind spot, the brain fills in the blank space based on the contents of the surrounding areas. While this is usually accurate enough, it means that our perception in the blind spot is objectively unreliable.
You can try it out by using this simple test (click the image to enlarge)

Keep your eyes fixed on the cross in (a). Close the left eye. Depending on the size & resolution of your screen, move your head slowly closer to (or sometimes further away from) the screen while looking at the cross. The dot in (a) should vanish. You can then try the same with the stimulus we used in this study (b). The small inset should vanish and you should perceive a continuous stimulus.

What we wanted to find out

To find out whether we are aware of the unreliable nature of stimuli in the blind spot we presented volunteers with two striped stimuli, one on each side of the screen. The center of some of the stimuli were covered by a patch that broke up the stripes. The volunteers’ task was to select the stimulus with uninterrupted stripes. The key to the experiment is that if the central patch appears in the blind spot, the brain will fill in the stripes so that they appear to be continuous. This means that the volunteers will have to choose between two stimuli that both appear to have continuous stripes.

A study participant chooses between two striped visual images, one ‘real’ and one inset in the blind spot, displayed using shutter glasses (CC-BY 4.0 Ricardo Gameiro)

The experimental setup. Only the case where the left stimulus is in the blind spot is shown here.

What we thought we would find

If subjects have no awareness of their blind spot, we might expect them to simply guess. Alternatively, if they are subconsciously aware that the stimulus in the blind spot is unreliable, they should choose the other one.

In reality, exactly the opposite happened:

The volunteers chose the blind spot stimulus more often than not. This suggests that information generated by the brain itself is sometimes treated as more reliable than sensory information from the outside world. Future experiments should examine whether the tendency to favor information generated within the brain over external sensory inputs is unique to the visual blind spot, or whether it also occurs elsewhere.

The results of the first experiment. Four subsequent experiments confirmed this finding.

Sources

All images are released under CC-BY 4.0.

Cite as: Ehinger et al.  “Humans treat unreliable filled-in percepts as more real than veridical ones”, eLife, doi: 10.7554/eLife.21761

EEGlab has ‘jet’ as the default colormap. But jet is pretty terrible

https://www.reddit.com/r/matlab/comments/1jqk8t/you_should_never_use_the_default_colors_in_matlab/

You see structure where there is none (e.g. rings in the third example).

The problem:

Eeglabs sets the default colormap to ‘jet’, thus overwriting a system wide default set e.g. by

“`

set(0,'DefaultFigureColormap',parula);

“`

It does so by calling “`icadefs.m “` in various functions (e.g. topoplot, erpimage) and defining:

“`

DEFAULT_COLORMAP = ‘jet’

“`

We want to overwrite the one line, but keep it forward compatible i.e. we do not want to copy the whole icadefs file, but just replace the single line whenever icadefs is called.

Solutions

Overwrite the line in icadefs.m default

This has the benefit that it will always work irrespective of your path-ordering. The con is, you will loose the change if you switch eeglab versions or update eeglab.

Change/create your eeglab “`eeg_options.txt“`.

This has the benefit that it will carry over to the next version of eeglab, but it is an extra file you need to have somewhere completly different than your project-folder (your user-folder ~/eeg_options.txt). It is thereby hard to make selfcontained code.

Make a new icadefs.m

Make a file called icadefs.m (this script will be called instead of the eeglab “`icadef“`) and add the following code:

“`

run([fileparts(which(‘eegrej’)) filesep ‘icadefs.m’]);
DEFAULT_COLORMAP = ‘parula’;

“`

This will call the original “`icadef“` (in the same folder as “`eegrej.m“` and then overwrite the eeglab-default

Important: The folder to your icadef file must be above eeglab in your path. 

Try this: “`edit(‘icadefs.m’)“` to see which function comes up. If the eeglab-one comes up you have a path conflict here. Your own “`icadefs“` has to be above the eeglab one.

In my “`project_init.m“` where I add all paths, I make sure that eeglab is started before adding the path to the new “`icadefs.m“`

Examples:

ICA – Topoplots of a single subject

Single component of an IC-Decomposition that included noisy data portions (and thus, I would say, is not usable)

I sometimes explain concepts to my students. Then I forget the code and the next time round, I have to redo it. Take this post as an extended memory-post. In this case I showed what filter-ringing artefacts could look like. This is especially important for EEG preprocessing where filtering is a standard procedure.

A good introduction to filtering can be found in this slides by andreas widmann or this paper by andreas widmann

Impulse with noise

I simulated as simple impulse response with some additional noise. The idea is to show the student that big spikes in the EEG-data could result in filter-ringing that is quite substantial and far away from the spike.

The filter

This is the filter I generated. It is a BAD filter. It shows huge passband ripples. But for educational purposes it suits me nice. I usually explain what passbands, transitionband, stopband, ripples and attenuation means.

The code

“`matlab
fs = 1000;
T = 2;
time = 0:1/fs:T-1/fs;

data = zeros(length(time),1);
% data(end/2:end) = data(end/2:end) + 1;
data(end/2) = data(end/2) + 1;
data = data + rand(size(data))*0.02;

subplot(2,1,1)
plot(data)

filtLow = designfilt(‘lowpassfir’,’PassbandFrequency’,100, …
‘StopbandFrequency’,110,’PassbandRipple’,0.5, …
‘StopbandAttenuation’,65,’SampleRate’,1000);

subplot(2,1,2)

% 0-padding to get the borders right
data = padarray(data,round(filtLow.filtord));

% Filter twice to get the same phase(non-causal)
a = filter(filtLow,data);
b = filter(filtLow,a(end:-1:1));
b = b(round(filtLow.filtord)+1:end – round(filtLow.filtord));
plot(b)

fvtool(filtLow) % to look at the filter

“`

TLDR;

52% of days it rained (Precipitation>0)

Is it sunny? 2x as likely that it is sunny tomorrow as well.

Is it rainy? 2.3x as likely that it is rainy tomorrow as well

Predicting rainfall using logistic regression

I’m playing around with some analyses for an upcoming course. This follows loosely the example of “Advanced Data Analysis from an Elemental Point of View” Chapter 12.7
It is a somewhat naive analysis. Further improvements are discussed at the end.

library(ggplot2)
library(plyr)

We load the data and change some of the German variables

# I downloaded the data from here:
# http://www.dwd.de/DE/leistungen/klimadatendeutschland/klimadatendeutschland.html
weather = data.frame(read.csv(file='produkt_klima_Tageswerte_19891001_20151231_01766.txt',sep=';'))
weather$date = as.Date.character(x=weather$MESS_DATUM,format="%Y%m%d")
weather = rename(weather,replace = c("NIEDERSCHLAGSHOEHE"="rain"))
weather$rain_tomorrow = c(tail(weather$rain,-1),NA)

weather <- weather[-nrow(weather),] # remove NA row
summary(weather[,c("date","rain","rain_tomorrow")])

##       date                 rain         rain_tomorrow    
##  Min.   :1989-10-01   Min.   :  0.000   Min.   :  0.000  
##  1st Qu.:1996-04-23   1st Qu.:  0.000   1st Qu.:  0.000  
##  Median :2002-11-15   Median :  0.100   Median :  0.100  
##  Mean   :2002-11-15   Mean   :  2.055   Mean   :  2.055  
##  3rd Qu.:2009-06-07   3rd Qu.:  2.200   3rd Qu.:  2.200  
##  Max.   :2015-12-30   Max.   :140.100   Max.   :140.100

The data range from 1989 up until the end of 2015.

p1= ggplot(weather,aes(x=rain))+geom_density()
cowplot::plot_grid(p1,p1+scale_x_log10())

Notice that the plot on the left is in native scale, the one on the right in x-axis-log-scale.
We take the mean of rainy days (ml/day > 0): There is a 52% probability it will rain on a given day (what everyone living in Osnabrück already knew, it rains more often than not).

Predicting rain from the day before

For exercise reasons I made several logistic regressions. I try to predict whether there will be rain on the day afterwards, based on the amount of rain on the current day.

m.weather.1 = glm(formula = rain_tomorrow>0 ~ rain>0,data=weather,family = "binomial")
summary(m.weather.1)

## 
## Call:
## glm(formula = rain_tomorrow > 0 ~ rain > 0, family = "binomial", 
##     data = weather)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5431  -0.8889   0.8514   0.8514   1.4965  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.72478    0.03136  -23.11   <2e-16 ***
## rain > 0TRUE  1.55287    0.04400   35.29   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 13278  on 9586  degrees of freedom
## Residual deviance: 11938  on 9585  degrees of freedom
## AIC: 11942
## 
## Number of Fisher Scoring iterations: 4

Whoop Whoop, Wald’s t-value of ~35! Keep in mind that the predictor values are in logit-space. That means, a predictor value of -0.72 is a log-odd value. In order to calculate this back to an easier interpreted format, we can simply take the exponential and receive the odds-ratio.

Do the calculations:

exp(coef(m.weather.1)[1])

## (Intercept) 
##   0.4844302

exp(sum(coef(m.weather.1))) # the odds for rain tomorrow if it is rainy (2 : 1)

## [1] 2.288933

Now we can interprete the odds:

The odds of rain tomorrow if there was a sunny day are 0.5:1, i.e. it is double as likely that the next day is sunny, if it was sunny today
The odds of rain tomorrow if it was a rainy day are 2.3:1, i.e. it is more than double as likely that the next day is rainy, if it was rainy today.

Can we get better?

We could try to predict rain based on the daily continuous precipitation (in ml).
We will compare this with the previous model using BIC (smaller number => better model).

m.weather.2 = glm(formula = rain_tomorrow>0 ~ rain,data=weather,family="binomial")
BIC(m.weather.1,m.weather.2)

##             df      BIC
## m.weather.1  2 11956.09
## m.weather.2  2 12505.85

Turns out: No, a categorical model (is there rain today, or not?) beats the continuous one. But why?

d.predNew = data.frame(rain=seq(0,50));
d.pred=             cbind(d.predNew,pred=arm::invlogit(predict(m.weather.2,newdata = d.predNew)),model='2')
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.1,newdata = d.predNew)),model='1'))

p1 = ggplot()+geom_point(data=d.pred,aes(x=rain,y=pred,color=model) )+ 
    geom_smooth(data=weather,aes(x=rain,y=(rain_tomorrow>0)*1))
cowplot::plot_grid(p1,p1+scale_x_log10())

We plot the predictions model 1 does in green, model 2 in red and the smoothed data in blue. On the left we have the x-axis in native units [ml?] on the right on log-scale. It is very clear, that the red dots do not match the empirical data (blue) at all. The green dots (model 1) are better. My guess is, this is due to some outlier influencing the slope, but also due to the non-homogenious distribution of rain-values as seen i the first figure
We will try two transformations off X (a log effect seems possible?)

• sqrt(rain)
• log(rain+0.001)

m.weather.3 = glm(formula = rain_tomorrow>0 ~ sqrt(rain),data=weather,family="binomial")
# Box-Cox transform with lambda2 = 0.001 http://robjhyndman.com/hyndsight/transformations/
m.weather.4 = glm(formula = rain_tomorrow>0 ~ log(rain+0.001),data=weather,family="binomial")


BIC(m.weather.1,m.weather.2,m.weather.3,m.weather.4)

##             df      BIC
## m.weather.1  2 11956.09
## m.weather.2  2 12505.85
## m.weather.3  2 12020.09
## m.weather.4  2 11795.15

It is surprisingly hard to beat the simple first model, but in the end – we did it! The log(rain) model seems to capture the data best.

d.predNew = data.frame(rain=seq(0,50));
d.pred=             cbind(d.predNew,pred=arm::invlogit(predict(m.weather.4,newdata = d.predNew)),model='2')
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.1,newdata = d.predNew)),model='1'))
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.3,newdata = d.predNew)),model='3'))
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.4,newdata = d.predNew)),model='4'))

p1 = ggplot()+geom_point(data=d.pred,aes(x=rain,y=pred,color=model) )+ 
    geom_smooth(data=weather,aes(x=rain,y=(rain_tomorrow>0)*1))
cowplot::plot_grid(p1,p1+scale_x_log10())

Visually we can see that model 4 comes the non-linear smoother the closest.

Improvements

• use nonlinear effects (GAM) as done in the book
• multivariate (make use of the plentitude of other information as well)
• use the months as a cyclical predictor, i.e. seasonal trends will be clearly present in the data

Misc

This post was directly exported using knit2wp and R-Markdown. It works kind of okay, but clearly the figures are not wide enough, even though I specify the correct width in the markdown. I might upload them later manually.