[matlab] performance for-loops vs. vectorization vs. bsxfun

From time to time I explain my students certain concepts. To archive those and as an extended memory, I share them here. We also recently had some discussion on vectorization in our research group. e.g. in python and matlab. With the second link claiming for-loops in matlab are performing much better than before.

Goal

Show that for-loops are still quite slow in matlab. Compare bsxfun against vectorized arithmetic expansion in matlab against bsxfun

The contenders

• good old for-loop: Easy to understand, can be found everywhere, slow
• arithmetic expansion: medium difficulty, should be general used, fast
• bsxfun: somewhat difficult to understand, I use it regularily, fast (often)

Comparisons

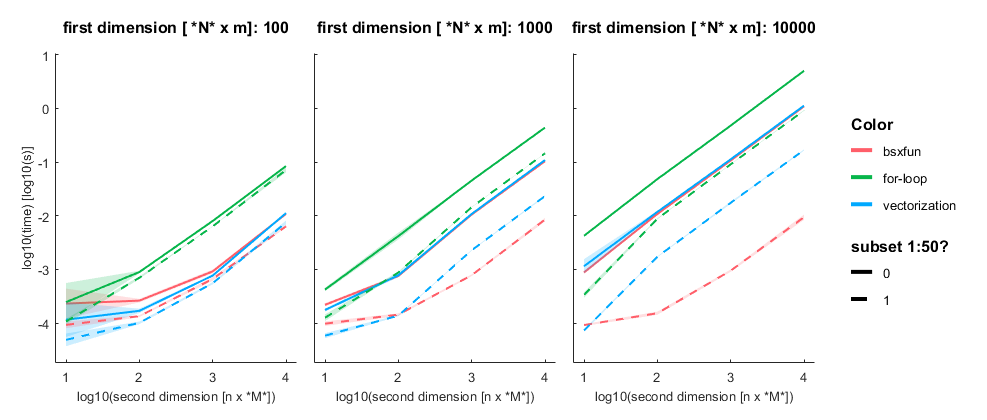
While demonstrating this to my student, I noticed that subsetting an array has interesting effects on the performance differences. The same is true for different array sizes. Therefore, I decided to systematically compare those.

I subtract one row from either a subset (first 50 rows, dashed line) or all rows of an [n x m] matrix with n= [100, 1000, 10 000] and m = [10, 100, 1000, 10 000]. Mean + SE

Three take home messages:

• for loop is very slow
• vectorization is fastest for small first dimension, then equally fast as bsxfun
• bsxfun is fastest if one needs to subset a medium sized array (n x m >100 x 1000), but see update below!

Update:

Prompted by Anne Urai, I redid the analysis with multiplication & devision. The pattern is the same. I did notice that allocating new matrices before doing the arithmetic expansion (vectorization) results in the same behaviour as bsxfun (but more lines of code)

A = data(ix,:);
B = data(1,:);
x = A./B;

matlab code

tAll = [];
for dim1 = [100 1000 10000]
    for dim2 = [10 100 1000 10000]
        tStart = tic;
        for subset = [0 1]
            if subset
                ix = 1:50;
            else
                ix = 1:dim1;
            end
            for run = 1:10
                data = rand(dim1,dim2);
                
                % for-loop
                x = data;
                tic
                for k= 1:size(data,2)
                    x(ix,k) = data(ix,k)-data(1,k);
                end
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'for-loop'},t)];
                %vectorized
                tic
                x = data(ix,:)-data(1,:);
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'vectorization'},t)];
                % bsxfun
                
                tic
                x= bsxfun(@minus,data(ix,:),data(1,:));
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'bsxfun'},t)];  
            end
        end
        fprintf('finished dim1=%i,dim2=%i - took me %.2fs\n',dim1,dim2,toc(tStart))
    end
end

% Plotting using the awesome GRAMM-toolbox
% https://github.com/piermorel/gramm
figure
g = gramm('x',log10(tAll.dim2),'y',log10(tAll.t),'color',tAll.Var4,'linestyle',tAll.subset);
g.facet_grid([],tAll.dim1)
g.stat_summary()
g.set_names('x','log10(second dimension [n x *M*])','y','log10(time) [log10(s)]','column','first dimension [ *N* x m]','linestyle','subset 1:50?')
g.draw()