From time to time I explain my students certain concepts. To archive those and as an extended memory, I share them here. We also recently had some discussion on vectorization in our research group. e.g. in python and matlab. With the second link claiming for-loops in matlab are performing much better than before.

Goal

Show that for-loops are still quite slow in matlab. Compare bsxfun against vectorized arithmetic expansion in matlab against bsxfun

The contenders

• good old for-loop: Easy to understand, can be found everywhere, slow
• arithmetic expansion: medium difficulty, should be general used, fast
• bsxfun: somewhat difficult to understand, I use it regularily, fast (often)

Comparisons

While demonstrating this to my student, I noticed that subsetting an array has interesting effects on the performance differences. The same is true for different array sizes. Therefore, I decided to systematically compare those.

I subtract one row from either a subset (first 50 rows, dashed line) or all rows of an [n x m] matrix with n= [100, 1000, 10 000] and m = [10, 100, 1000, 10 000]. Mean + SE

Three take home messages:

• for loop is very slow
• vectorization is fastest for small first dimension, then equally fast as bsxfun
• bsxfun is fastest if one needs to subset a medium sized array (n x m >100 x 1000), but see update below!

Update:

Prompted by Anne Urai, I redid the analysis with multiplication & devision. The pattern is the same. I did notice that allocating new matrices before doing the arithmetic expansion (vectorization) results in the same behaviour as bsxfun (but more lines of code)

A = data(ix,:);
B = data(1,:);
x = A./B;

matlab code

tAll = [];
for dim1 = [100 1000 10000]
    for dim2 = [10 100 1000 10000]
        tStart = tic;
        for subset = [0 1]
            if subset
                ix = 1:50;
            else
                ix = 1:dim1;
            end
            for run = 1:10
                data = rand(dim1,dim2);
                
                % for-loop
                x = data;
                tic
                for k= 1:size(data,2)
                    x(ix,k) = data(ix,k)-data(1,k);
                end
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'for-loop'},t)];
                %vectorized
                tic
                x = data(ix,:)-data(1,:);
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'vectorization'},t)];
                % bsxfun
                
                tic
                x= bsxfun(@minus,data(ix,:),data(1,:));
                t = toc;
                tAll = [tAll; table(dim1,dim2,subset,{'bsxfun'},t)];  
            end
        end
        fprintf('finished dim1=%i,dim2=%i - took me %.2fs\n',dim1,dim2,toc(tStart))
    end
end

% Plotting using the awesome GRAMM-toolbox
% https://github.com/piermorel/gramm
figure
g = gramm('x',log10(tAll.dim2),'y',log10(tAll.t),'color',tAll.Var4,'linestyle',tAll.subset);
g.facet_grid([],tAll.dim1)
g.stat_summary()
g.set_names('x','log10(second dimension [n x *M*])','y','log10(time) [log10(s)]','column','first dimension [ *N* x m]','linestyle','subset 1:50?')
g.draw()

I got asked for the design of my academic posters. Indeed I have templates in landscape and portrait and I’m happy to share them. In addition I can recommend the blog better-posters which has regularily features and link-roundups on poster-design related things.

In my newest poster (landscape below) I tried to move as much text to the side, so that people can still understand the poster, but it does not obscure the content. I also really like the 15s summary, an easy way to see whether you will like the poster, or you can simply move on. Maybe it even needs to be a 5s summary!

These are two examples posters based on my template.

Neat Features

Titles’ backgrounds follow along

This is useful because you do not manually need to resize the white background of the text that overlays on the borders

Borders are effects, easy resizing

The corners are based on illustrator effects, thus resizing the containers does not change the curvature. Before I often had very strange curvatures in my boxes. No more!

Download here

Portrait Equal Columns (ai-template, 0.3mb)

Portrait Unequal Columns (ai-template, 0.3mb)

Landscape (ai-template, 0.4mb)

Licence is CC-4.0, you can aknowledge me if you want, but no need if you don’t 🙂

We recently published an article (free to read): “Humans treat unreliable filled-in percepts as more real than veridical ones”. Inspired by Selim Onat and many others, I try to to explain the main findings in plain language. First let me give you some background:

To make sense of the world around us, we must combine information from multiple sources while taking into account how reliable they are. When crossing the street, for example, we usually rely more on input from our eyes than our ears. However we can reassess our reliability estimate: on a foggy day with poor visibility, we might prioritize listening for traffic instead.

The human blind spots

But how do we assess the reliability of information generated within the brain itself? We are able to see because the brain constructs an image based on the patterns of activity of light-sensitive proteins in a part of the eye called the retina. However, there is a point on the retina where the presence of the optic nerve leaves no space for light-sensitive receptors. This means there is a corresponding point in our visual field where the brain receives no visual input from the outside world. To prevent us from perceiving this gap, known as the visual blind spot, the brain fills in the blank space based on the contents of the surrounding areas. While this is usually accurate enough, it means that our perception in the blind spot is objectively unreliable.
You can try it out by using this simple test (click the image to enlarge)

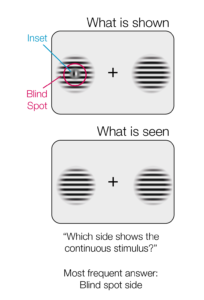
Keep your eyes fixed on the cross in (a). Close the left eye. Depending on the size & resolution of your screen, move your head slowly closer to (or sometimes further away from) the screen while looking at the cross. The dot in (a) should vanish. You can then try the same with the stimulus we used in this study (b). The small inset should vanish and you should perceive a continuous stimulus.

What we wanted to find out

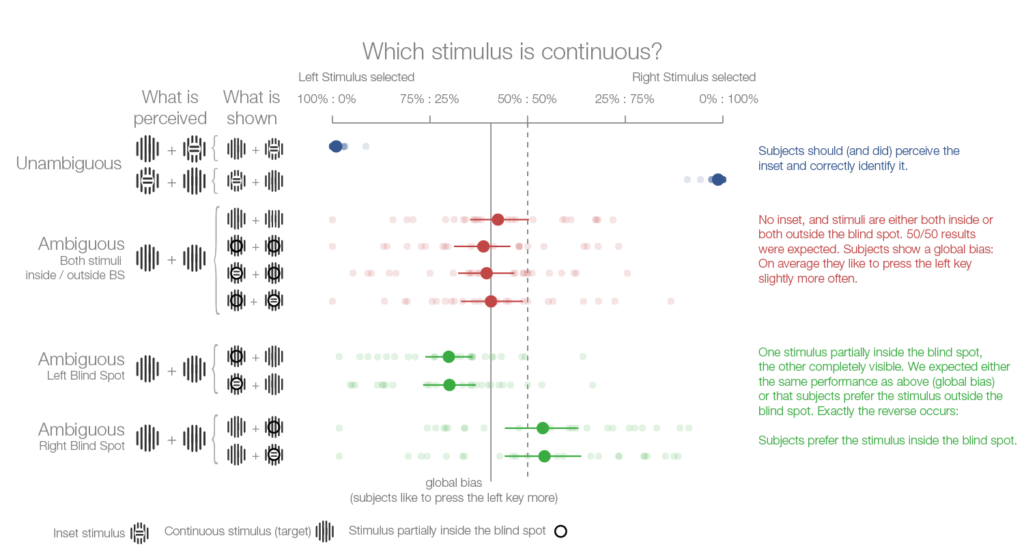
To find out whether we are aware of the unreliable nature of stimuli in the blind spot we presented volunteers with two striped stimuli, one on each side of the screen. The center of some of the stimuli were covered by a patch that broke up the stripes. The volunteers’ task was to select the stimulus with uninterrupted stripes. The key to the experiment is that if the central patch appears in the blind spot, the brain will fill in the stripes so that they appear to be continuous. This means that the volunteers will have to choose between two stimuli that both appear to have continuous stripes.

A study participant chooses between two striped visual images, one ‘real’ and one inset in the blind spot, displayed using shutter glasses (CC-BY 4.0 Ricardo Gameiro)

The experimental setup. Only the case where the left stimulus is in the blind spot is shown here.

What we thought we would find

If subjects have no awareness of their blind spot, we might expect them to simply guess. Alternatively, if they are subconsciously aware that the stimulus in the blind spot is unreliable, they should choose the other one.

In reality, exactly the opposite happened:

The volunteers chose the blind spot stimulus more often than not. This suggests that information generated by the brain itself is sometimes treated as more reliable than sensory information from the outside world. Future experiments should examine whether the tendency to favor information generated within the brain over external sensory inputs is unique to the visual blind spot, or whether it also occurs elsewhere.

The results of the first experiment. Four subsequent experiments confirmed this finding.

Sources

All images are released under CC-BY 4.0.

Cite as: Ehinger et al.  “Humans treat unreliable filled-in percepts as more real than veridical ones”, eLife, doi: 10.7554/eLife.21761

EEGlab has ‘jet’ as the default colormap. But jet is pretty terrible

https://www.reddit.com/r/matlab/comments/1jqk8t/you_should_never_use_the_default_colors_in_matlab/

You see structure where there is none (e.g. rings in the third example).

The problem:

Eeglabs sets the default colormap to ‘jet’, thus overwriting a system wide default set e.g. by

“`

set(0,'DefaultFigureColormap',parula);

“`

It does so by calling “`icadefs.m “` in various functions (e.g. topoplot, erpimage) and defining:

“`

DEFAULT_COLORMAP = ‘jet’

“`

We want to overwrite the one line, but keep it forward compatible i.e. we do not want to copy the whole icadefs file, but just replace the single line whenever icadefs is called.

Solutions

Overwrite the line in icadefs.m default

This has the benefit that it will always work irrespective of your path-ordering. The con is, you will loose the change if you switch eeglab versions or update eeglab.

Change/create your eeglab “`eeg_options.txt“`.

This has the benefit that it will carry over to the next version of eeglab, but it is an extra file you need to have somewhere completly different than your project-folder (your user-folder ~/eeg_options.txt). It is thereby hard to make selfcontained code.

Make a new icadefs.m

Make a file called icadefs.m (this script will be called instead of the eeglab “`icadef“`) and add the following code:

“`

run([fileparts(which(‘eegrej’)) filesep ‘icadefs.m’]);
DEFAULT_COLORMAP = ‘parula’;

“`

This will call the original “`icadef“` (in the same folder as “`eegrej.m“` and then overwrite the eeglab-default

Important: The folder to your icadef file must be above eeglab in your path. 

Try this: “`edit(‘icadefs.m’)“` to see which function comes up. If the eeglab-one comes up you have a path conflict here. Your own “`icadefs“` has to be above the eeglab one.

In my “`project_init.m“` where I add all paths, I make sure that eeglab is started before adding the path to the new “`icadefs.m“`

Examples:

ICA – Topoplots of a single subject

Single component of an IC-Decomposition that included noisy data portions (and thus, I would say, is not usable)

I sometimes explain concepts to my students. Then I forget the code and the next time round, I have to redo it. Take this post as an extended memory-post. In this case I showed what filter-ringing artefacts could look like. This is especially important for EEG preprocessing where filtering is a standard procedure.

A good introduction to filtering can be found in this slides by andreas widmann or this paper by andreas widmann

Impulse with noise

I simulated as simple impulse response with some additional noise. The idea is to show the student that big spikes in the EEG-data could result in filter-ringing that is quite substantial and far away from the spike.

The filter

This is the filter I generated. It is a BAD filter. It shows huge passband ripples. But for educational purposes it suits me nice. I usually explain what passbands, transitionband, stopband, ripples and attenuation means.

The code

“`matlab
fs = 1000;
T = 2;
time = 0:1/fs:T-1/fs;

data = zeros(length(time),1);
% data(end/2:end) = data(end/2:end) + 1;
data(end/2) = data(end/2) + 1;
data = data + rand(size(data))*0.02;

subplot(2,1,1)
plot(data)

filtLow = designfilt(‘lowpassfir’,’PassbandFrequency’,100, …
‘StopbandFrequency’,110,’PassbandRipple’,0.5, …
‘StopbandAttenuation’,65,’SampleRate’,1000);

subplot(2,1,2)

% 0-padding to get the borders right
data = padarray(data,round(filtLow.filtord));

% Filter twice to get the same phase(non-causal)
a = filter(filtLow,data);
b = filter(filtLow,a(end:-1:1));
b = b(round(filtLow.filtord)+1:end – round(filtLow.filtord));
plot(b)

fvtool(filtLow) % to look at the filter

“`

TLDR;

52% of days it rained (Precipitation>0)

Is it sunny? 2x as likely that it is sunny tomorrow as well.

Is it rainy? 2.3x as likely that it is rainy tomorrow as well

Predicting rainfall using logistic regression

I’m playing around with some analyses for an upcoming course. This follows loosely the example of “Advanced Data Analysis from an Elemental Point of View” Chapter 12.7
It is a somewhat naive analysis. Further improvements are discussed at the end.

library(ggplot2)
library(plyr)

We load the data and change some of the German variables

# I downloaded the data from here:
# http://www.dwd.de/DE/leistungen/klimadatendeutschland/klimadatendeutschland.html
weather = data.frame(read.csv(file='produkt_klima_Tageswerte_19891001_20151231_01766.txt',sep=';'))
weather$date = as.Date.character(x=weather$MESS_DATUM,format="%Y%m%d")
weather = rename(weather,replace = c("NIEDERSCHLAGSHOEHE"="rain"))
weather$rain_tomorrow = c(tail(weather$rain,-1),NA)

weather <- weather[-nrow(weather),] # remove NA row
summary(weather[,c("date","rain","rain_tomorrow")])

##       date                 rain         rain_tomorrow    
##  Min.   :1989-10-01   Min.   :  0.000   Min.   :  0.000  
##  1st Qu.:1996-04-23   1st Qu.:  0.000   1st Qu.:  0.000  
##  Median :2002-11-15   Median :  0.100   Median :  0.100  
##  Mean   :2002-11-15   Mean   :  2.055   Mean   :  2.055  
##  3rd Qu.:2009-06-07   3rd Qu.:  2.200   3rd Qu.:  2.200  
##  Max.   :2015-12-30   Max.   :140.100   Max.   :140.100

The data range from 1989 up until the end of 2015.

p1= ggplot(weather,aes(x=rain))+geom_density()
cowplot::plot_grid(p1,p1+scale_x_log10())

Notice that the plot on the left is in native scale, the one on the right in x-axis-log-scale.
We take the mean of rainy days (ml/day > 0): There is a 52% probability it will rain on a given day (what everyone living in Osnabrück already knew, it rains more often than not).

Predicting rain from the day before

For exercise reasons I made several logistic regressions. I try to predict whether there will be rain on the day afterwards, based on the amount of rain on the current day.

m.weather.1 = glm(formula = rain_tomorrow>0 ~ rain>0,data=weather,family = "binomial")
summary(m.weather.1)

## 
## Call:
## glm(formula = rain_tomorrow > 0 ~ rain > 0, family = "binomial", 
##     data = weather)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5431  -0.8889   0.8514   0.8514   1.4965  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.72478    0.03136  -23.11   <2e-16 ***
## rain > 0TRUE  1.55287    0.04400   35.29   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 13278  on 9586  degrees of freedom
## Residual deviance: 11938  on 9585  degrees of freedom
## AIC: 11942
## 
## Number of Fisher Scoring iterations: 4

Whoop Whoop, Wald’s t-value of ~35! Keep in mind that the predictor values are in logit-space. That means, a predictor value of -0.72 is a log-odd value. In order to calculate this back to an easier interpreted format, we can simply take the exponential and receive the odds-ratio.

Do the calculations:

exp(coef(m.weather.1)[1])

## (Intercept) 
##   0.4844302

exp(sum(coef(m.weather.1))) # the odds for rain tomorrow if it is rainy (2 : 1)

## [1] 2.288933

Now we can interprete the odds:

The odds of rain tomorrow if there was a sunny day are 0.5:1, i.e. it is double as likely that the next day is sunny, if it was sunny today
The odds of rain tomorrow if it was a rainy day are 2.3:1, i.e. it is more than double as likely that the next day is rainy, if it was rainy today.

Can we get better?

We could try to predict rain based on the daily continuous precipitation (in ml).
We will compare this with the previous model using BIC (smaller number => better model).

m.weather.2 = glm(formula = rain_tomorrow>0 ~ rain,data=weather,family="binomial")
BIC(m.weather.1,m.weather.2)

##             df      BIC
## m.weather.1  2 11956.09
## m.weather.2  2 12505.85

Turns out: No, a categorical model (is there rain today, or not?) beats the continuous one. But why?

d.predNew = data.frame(rain=seq(0,50));
d.pred=             cbind(d.predNew,pred=arm::invlogit(predict(m.weather.2,newdata = d.predNew)),model='2')
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.1,newdata = d.predNew)),model='1'))

p1 = ggplot()+geom_point(data=d.pred,aes(x=rain,y=pred,color=model) )+ 
    geom_smooth(data=weather,aes(x=rain,y=(rain_tomorrow>0)*1))
cowplot::plot_grid(p1,p1+scale_x_log10())

We plot the predictions model 1 does in green, model 2 in red and the smoothed data in blue. On the left we have the x-axis in native units [ml?] on the right on log-scale. It is very clear, that the red dots do not match the empirical data (blue) at all. The green dots (model 1) are better. My guess is, this is due to some outlier influencing the slope, but also due to the non-homogenious distribution of rain-values as seen i the first figure
We will try two transformations off X (a log effect seems possible?)

• sqrt(rain)
• log(rain+0.001)

m.weather.3 = glm(formula = rain_tomorrow>0 ~ sqrt(rain),data=weather,family="binomial")
# Box-Cox transform with lambda2 = 0.001 http://robjhyndman.com/hyndsight/transformations/
m.weather.4 = glm(formula = rain_tomorrow>0 ~ log(rain+0.001),data=weather,family="binomial")


BIC(m.weather.1,m.weather.2,m.weather.3,m.weather.4)

##             df      BIC
## m.weather.1  2 11956.09
## m.weather.2  2 12505.85
## m.weather.3  2 12020.09
## m.weather.4  2 11795.15

It is surprisingly hard to beat the simple first model, but in the end – we did it! The log(rain) model seems to capture the data best.

d.predNew = data.frame(rain=seq(0,50));
d.pred=             cbind(d.predNew,pred=arm::invlogit(predict(m.weather.4,newdata = d.predNew)),model='2')
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.1,newdata = d.predNew)),model='1'))
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.3,newdata = d.predNew)),model='3'))
d.pred=rbind(d.pred,cbind(d.predNew,pred=arm::invlogit(predict(m.weather.4,newdata = d.predNew)),model='4'))

p1 = ggplot()+geom_point(data=d.pred,aes(x=rain,y=pred,color=model) )+ 
    geom_smooth(data=weather,aes(x=rain,y=(rain_tomorrow>0)*1))
cowplot::plot_grid(p1,p1+scale_x_log10())

Visually we can see that model 4 comes the non-linear smoother the closest.

Improvements

• use nonlinear effects (GAM) as done in the book
• multivariate (make use of the plentitude of other information as well)
• use the months as a cyclical predictor, i.e. seasonal trends will be clearly present in the data

Misc

This post was directly exported using knit2wp and R-Markdown. It works kind of okay, but clearly the figures are not wide enough, even though I specify the correct width in the markdown. I might upload them later manually.

I tried adding a bi-modal prior in STAN for a homework exercise on Bayesian Data Analysis. At first, I thought this could work:
“`STAN
model{
mu ~ normal(-0.5,0.3) + normal(0.5,0.3);
}
“`
But it doesn’t. I had to dig deeper and I thought I could simply add multiple times to the log-posterior due to a sideremark of Bob Carpenter:

“`STAN
target += normal_lpdf(mu|.5,0.3);
target += normal_lpdf(mu|-.5,0.3);
“`
Which also does not work. Finally, the solution is akin to the mixture model in the STAN manual:

“`STAN
target += log_sum_exp(normal_lpdf(mu|.5,0.3),normal_lpdf(mu|-.5,0.3));
“`

This results in beautiful bi-modal priors:

I did not find anything on google or the manual of how to do this. If there is a smarter way to do it, please leave a comment.

“`R

library(rstan)

model <- " data { } parameters { real mu; } transformed parameters { } model { //mu ~ normal(10,1); //mu ~ normal(-10,1); target += log_sum_exp(normal_lpdf(mu|-.5,.3),normal_lpdf(mu|.5,.3)); }" samples <- stan(model_code=model, iter=2000, chains=4, thin=1, # seed=123 # Setting seed; Default is random seed ) ggmcmc::ggs_density(ggmcmc::ggs(samples))+theme_minimal() ```

I made some graphs that show the relation between X1~X2 (X2 predicts X1), X2~X1 (X1 predicts X2) and the first principal component (direction with highest variance, also called total least squares).

The line you fit with a principal component is not the same line as in a regression (either predicting X2 by X1 [X2~X1] or X1 by X2 [X1~X2]. This is quite well known (see references below).

With regression one predicts X2 based on X1 (X2~X1 in R-Formula writing) or vice versa. With principal component (or total least squares) one tries to quantify the relation between the two. To completely understand the difference, image what quantity is reduced in the three cases.

In regression, we reduce the residuals in direction of the dependent variable. With principal components, we find the line, that has the smallest error orthogonal to the regression line. See the following image for a visual illustration.

For me it becomes interesting if you plot a scatter plot of two independent variables, i.e. you would usually report the correlation coefficient. The ‘correct’ line accompaniyng the correlation coefficient would be the principal component (‘correct’ as it is also agnostic to the order of the signals).

Further information:

How to draw the line, eLife 2013
Gelman, Hill – Data Analysis using Regression, p.58
Also check out the nice blogpost from Martin Johnsson doing practically the same thing but three years earlier 😉

Source

“`R
library(ggplot2)
library(magrittr)
library(plyr)

set.seed(2)
corrCoef = 0.5 # sample from a multivariate normal, 10 datapoints
dat = MASS::mvrnorm(10,c(0,0),Sigma = matrix(c(1,corrCoef,2,corrCoef),2,2))
dat[,1] = dat[,1] – mean(dat[,1]) # it makes life easier for the princomp
dat[,2] = dat[,2] – mean(dat[,2])

dat = data.frame(x1 = dat[,1],x2 = dat[,2])

# Calculate the first principle component
# see http://stats.stackexchange.com/questions/13152/how-to-perform-orthogonal-regression-total-least-squares-via-pca
v = dat%>%prcomp%$%rotation
x1x2cor = bCor = v[2,1]/v[1,1]

x1tox2 = coef(lm(x1~x2,dat))
x2tox1 = coef(lm(x2~x1,dat))
slopeData =data.frame(slope = c(x1x2cor,1/x1tox2[2],x2tox1[2]),type=c(‘Principal Component’,’X1~X2′,’X2~X1′))

# We want this to draw the neat orthogonal lines.
pointOnLine = function(inp){
# y = a*x + c (c=0)
# yOrth = -(1/a)*x + d
# yOrth = b*x + d
x0 = inp[1] y0 = inp[2] a = x1x2cor
b = -(1/a)
c = 0
d = y0 – b*x0
x = (d-c)/(a-b)
y = -(1/a)*x+d
return(c(x,y))
}
points = apply(dat,1,FUN=pointOnLine)

segmeData = rbind(data.frame(x=dat[,1],y=dat[,2],xend=points[1,],yend=points[2,],type = ‘Principal Component’),
data.frame(x=dat[,1],y=dat[,2],yend=dat[,1]*x2tox1[2],xend=dat[,1],type=’X2~X1′),
data.frame(x=dat[,1],y=dat[,2],yend=dat[,2],xend=dat[,2]*x1tox2[2],type=’X1~X2′))

ggplot(aes(x1,x2),data=dat)+geom_point()+
geom_abline( data=slopeData,aes(slope = slope,intercept=0,color=type))+
theme_minimal(20)+coord_equal()

ggplot(aes(x1,x2),data=dat)+geom_point()+
geom_abline( data=slopeData,aes(slope = slope,intercept=0,color=type))+
geom_segment(data=segmeData,aes(x=x,y=y,xend=xend,yend=yend,color=type))+facet_grid(.~type)+coord_equal()+theme_minimal(20)
“`

The problem

It is commonly accepted that axes of plots should align if data needs to be compared between subplots. But the default way on how multiple topoplots are plotted violates this principle. While usually the limits of the colormap are kept constant for all colormaps, the contours rarely are. This default plot looks similar to this one:

The solution

It is simple, keep the contours constant!

In eeglab this is done using the topoplot function with the argument 'numcontours', linspace(-scale,scale,n_contours) or similar. You can also use my new plotting script available here on github
So if we would keep the values constant at which contours are generated it looks like this:

More ideas

Each topoplot has its individual color-limits. While the local (in a single topoplot) extremata a clearly visible, not much to compare between topoplots

Individual contours improve the readability of each map, but they do not add anything that eases the comparison.

Forcing the same color-limits in the colormap allows for direct comparison between topoplots. But whether the white of the 9th’s or the 12th’s topoplot is bigger is hard to tell.

Going back to individual colormaps, but keeping the same contours: This helps already a lot, I seem to abstract the colormap away a bit and use the contours for comparison

The opposite way, same color-limits but individual contours. Again I seem to rely more on the contours, in this case this is more confusing than before.

In the final plot colormap and contour are aligned. This enhances comparison between topoplots.

One problem with the same color-limits or the same contour lines between topoplots is, that large deflections could hide small ones. As in many cases, it depends on what features of the data you want to highlight. I recommend the final plot where contour and colormap align as the default.

Conclusion

If you are plotting multiple topoplots, try to keep the color-limits of the colormap as well as the contour levels constant

Goal

Give a graphical representation of multitaper time frequency parameters.

Background

Frequency Resolution and sFFT

In M/EEG analysis we are often interested in oscillations. One tool to analyse oscillations is by using time-frequency methods. In principle they work by segmenting the signal of interest in small windows and calculating a spectrum for each window. A tutorial can be found on the fieldtrip page. There exists a time-frequency tradeof: $\delta f = \frac{1}{T}$ with T the timewindow (in s) and $\delta f$ the frequency resolution. The percentage-difference of two neighbouring frequency resolution gets smaller the higher the frequency goes, e.g. a $\delta f$ of 1 at 2Hz and 3Hz is 50%, but the same difference at 100Hz and 101Hz is only 1%. Thus usually we try to decrease the frequency resolution the higher we go. A popular examples are wavelets, they inherently do this. One problem with wavelets is, that the parameters are not perfectly intuitive (I find). I prefer to use short-time FFT, and a special flavour the Multitaper.

Multitaper

We can sacrifice time or frequency resolution for SNR. I.e. one can average estimates at neighbouring timewindows or estimates at neighbouring frequencies. A smart way to do this is to use multitapers, I will not go into details here. In the end, they allow us to average smartly over time or frequency.

Parameter one usually specifies

• foi: The frequencies of interest. Note that you can use arbitrary high resolution but if you have $\delta foi < \delta f$ then information will be displayed redundantly (but it looks smoother).
• tapsmofrq: How much frequency smoothing should happen at each foi.
• t_ftimwin: The timewindow for each foi

Plotting the parameters

With the matlab-function attached to the end of the post one can see the effective frequency-resolution of the parameters in a single plot. For this example I use the frequency parameters by Hipp 2011. They logarithmically scale up the frequencybandwith. In order to do so for the low frequencies (1-16Hz) they change the size of the timewindow, for the higher frequencies they use multitaper with a constant window size of 250ms.

This is the theoretical resolution (interactive graph), i.e. a plot of the parameters you put in. foi +- tapsmofrq scaled by each timewindow size. Note: The individual bar size depicts the window-size of the respective frequency-bin.

This is the numeric resolution (interactice graph). I used the frequency response of 100 repetitions of white noise (flat spectrum over repetitions) and calculated the frequency response of the multitaper filters. This is scaled in the x-axis by the time-window used.

Check out the interactive graphs to see how the time-windows change as intendet with lower frequencies.

The colorbar depict the number of tapers used. As intended, the number of tapers do not change from 1-16Hz.

Code

function [] = plot_taper(inpStruct,cfg)
%% plot_taper
% inpStruct: All fields need to have the same length
%   foi       : The frequencies of interest.    
%   tapsmofrq : How much frequency smoothing should happen at each foi (+-tapsmofrq)
%   t_ftimwin : The timewindow for each foi
% You can also directly input a fieldtrip time-freq object
%
% cfg:
%   logy      : plot the y-axis as log10
%   type      : "theoretical" : This plots the foi+-tapsmofrq
%               "numerical"   : Simulation of white noise to approx the
%               effective resolution

if nargin == 1
    cfg = struct();
end

if isfield(cfg,'logy')
    assert(ismember(cfg.type,[0,1]),'logy has to be 0 or 1')
    logy = cfg.logy;
else 
    logy = 0;
end
if isfield(cfg,'type')
    assert(ismember(cfg.type,{'numerical','theoretical'}),'type has to be ''numerical'' or ''theoretical''')
    type = cfg.type;

else
   type = 'numerical'; 
end
nRep = 100; % repetitions of the numeric condition
xscaling = 0.5;
if ~isempty(inpStruct) && isfield(inpStruct,'t_ftimwin')
    fprintf('cfg detected\n')
    cfg = inpStruct;
elseif ~isempty(inpStruct) && isfield(inpStruct,'cfg')
    fprintf('fieldtrip structure detected\n')
    cfg = inpStruct.cfg;
else
    fprintf('using parameters from Hipp 2010 Neuron \n')
    cfg =[];

    % we use logspaced frequencies from 4 to 181 Hz
    cfg.foi = logspace(log10(4),log10(181),23);

    % The windows should have 3/4 octave smoothing in frequency domain
    cfg.tapsmofrq = (cfg.foi*2^(3/4/2) - cfg.foi*2^(-3/4/2)) /2; % /2 because fieldtrip takes +- tapsmofrq

    % The timewindow should be so, that for freqs below 16, it results in n=1
    % Taper used, but for frequencies higher, it should be a constant 250ms.
    % To get the number of tapers we use:  round(cfg.tapsmofrq*2.*cfg.t_ftimwin-1)
    cfg.t_ftimwin = [2./(cfg.tapsmofrq(cfg.foi<16)*2),repmat(0.25,1,length(cfg.foi(cfg.foi>=16)))];
end

max_tapers = ceil(max(cfg.t_ftimwin.*cfg.tapsmofrq*2));
color_tapers = parula(max_tapers);
%%
figure
for fIdx = 1:length(cfg.t_ftimwin)
    timwin = cfg.t_ftimwin(fIdx);
    tapsmofrq = cfg.tapsmofrq(fIdx); % this is the fieldtrip standard, +- the taper frequency
    freqoi = cfg.foi(fIdx);
    switch type
        case 'theoretical'
            % This part simply plots the parameters as requested by the
            % user.
            y = ([freqoi-tapsmofrq freqoi+tapsmofrq freqoi+tapsmofrq freqoi-tapsmofrq]);

            ds = 0.3;
            ys = ([freqoi-ds freqoi+ds freqoi+ds freqoi-ds]);
            if logy
                y = log10(y);
                ys = log10(ys);
            end
            x = [-timwin/2 -timwin/2 +timwin/2 +timwin/2]+fIdx*xscaling;

            patch(x,y,color_tapers(round(2*timwin*tapsmofrq),:),'FaceAlpha',.7)
            patch(x,ys,[0.3 1 0.3],'FaceAlpha',.5)
        case 'numerical'
            fsample = 1000; % sample Fs 
            % This part is copied together from ft_specest_mtmconvol
            timwinsample = round(timwin .* fsample); % the number of samples in the timewin

            % get the tapers
            tap = dpss(timwinsample, timwinsample .* (tapsmofrq ./ fsample))';
            tap = tap(1:(end-1), :); % the kill the last one because 'it is weird'

            % don't fully understand, something about keeping the phase
            anglein  = (-(timwinsample-1)/2 : (timwinsample-1)/2)'   .*  ((2.*pi./fsample) .* freqoi);

            % The general idea (I think) is that instead of windowing the
            % time-signal and shifting the wavelet per timestep, we can multiply the frequency representation of
            % wavelet and the frequency representation of the data. this
            % masks all non-interesting frequencies and we can go back to
            % timespace and select the portions of interest. In formula:
            % ifft(fft(signal).*fft(wavelet))
            %
            % here we generate the wavelets by windowing sin/cos with the
            % tapers. We then calculate the spectrum
            wltspctrm = [];
            for itap = 1:size(tap,1)
                coswav  = tap(itap,:) .* cos(anglein)';
                sinwav  = tap(itap,:) .* sin(anglein)';
                wavelet = complex(coswav, sinwav);
                % store the fft of the complex wavelet
                wltspctrm(itap,:) = fft(wavelet,[],2);
            end


%           % We do this nRep times because a single random vector does not
%           have a flat spectrum.
            datAll = nan(nRep,timwinsample);
            for rep = 1:nRep
                sig = randi([0 1],timwinsample,1)*2-1; %http://dsp.stackexchange.com/questions/13194/matlab-white-noise-with-flat-constant-power-spectrum
                spec = bsxfun(@times,fft(sig),wltspctrm'); % multiply the spectra 
                datAll(rep,:) = sum(abs(spec),2); %save only the power
            end
            dat = mean(datAll); %average over reps


            % normalize the power
            dat = dat- min(dat);
            dat = dat./max(dat);

            t0 = 0 + fIdx*xscaling;
            t = t0 + dat*timwin/2;
            tNeg = t0 - dat*timwin/2;

            f = linspace(0,fsample-1/timwin,timwinsample);%0:1/timwin:fsample-1;
            if logy
                f = log10(f);
            end
            % this is a bit hacky violin plot, but looks good.
            patch([t tNeg(end:-1:1)],[f f(end:-1:1)],color_tapers(2*round(timwin*tapsmofrq),:),'FaceAlpha',.7)
    end


end
c= colorbar;colormap('parula')
c.Label.String = '# Tapers Used';
caxis([1 size(color_tapers,1)])

set(gca,'XTicks',[0,1])
xlabel('width of plot depicts window size in [s]')
if logy
    set(gca,'ylim',[0 log(max(1.2*(cfg.foi+cfg.tapsmofrq)))]);
    ylabel('frequency [log(Hz)]')
else
    set(gca,'ylim',[0 max(1.2*(cfg.foi+cfg.tapsmofrq))]);
    ylabel('frequency [Hz]')
end
end