I had this blog post as a draft for nearly a year now… and finally here it is: In my last lab we moved buildings. Good scientists we are we did measurements to see if the system works as intended…

The EEG Systems

• • An active 64 electrode system from BrainProducts called ActiCap
  • A passive 128 electrode system from ANT, a tmsi REFA-8 with actively shielded cables
  • A passive 128 electrode system from ANT, eegosport with actively shielded cables

Disclaimer: All data shown here are from different subjects. Their individual alpha-peaks etc. will differ, we also switched methods a bit

ActiCap

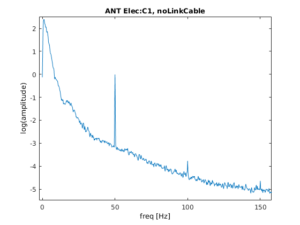
We measured 2 subjects with the 64 electrode system. When we checked the frequency spectrum we were very worried.

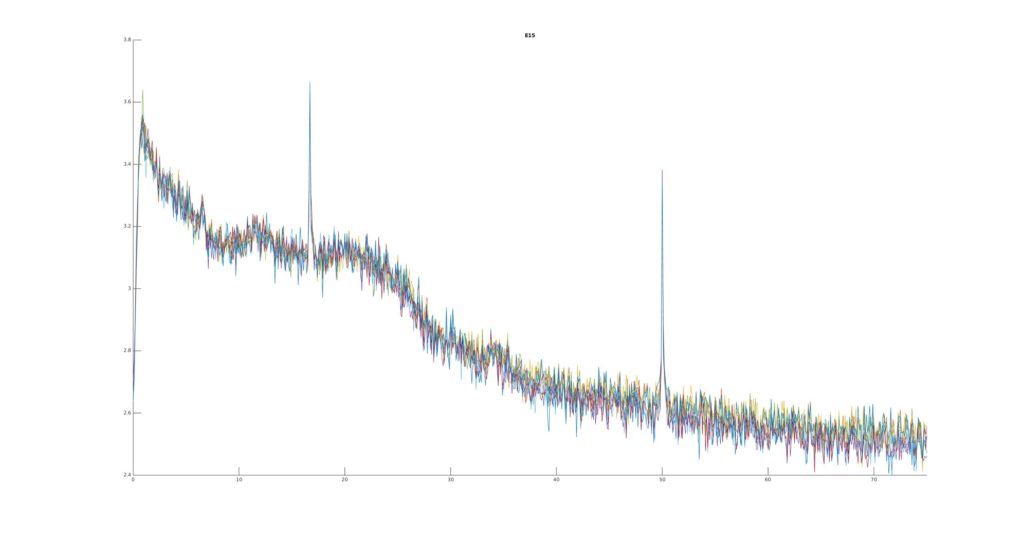
Besides the typical 50Hz artefact that we know, one can clearly see a $16 \frac{2}{3}$ Hz peak in the beta-band. The artefact is very strong and variable over time.

This can’t be right? So we recorded another subject, just to be sure. We also switched analysis methods a bit

Same thing!

Side remark: The ‘activeShield’ button did not improve the shielding (plots not shown, the support told us that the activeShield function is more thought for passive electrode systems, not our system).

ANT/TMSI REFA-8

Single Amplifier (64 Electrodes)

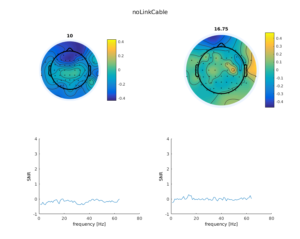
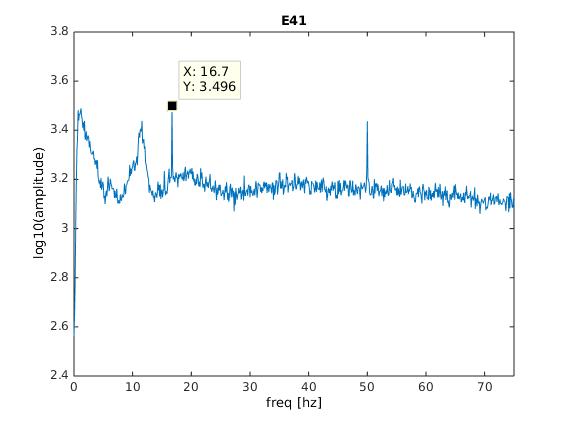
We then measured a single subject with the ANT system with a single amplifier.

All looks fine here for now… On the second plot, we introduce the signal-to-noise (SNR) index, which is simply the current frequency-bin divided by neighbouring bins (the average of $n_{-12}$:$n_{-2}$ & $n_{+2}$:$n_{+12}$). This will enhance peaks in the spectrum. As we can see, we do not see any peaks anywhere, all is fine with 64 electrodes.

Two Amplifiers (128 Electrodes)

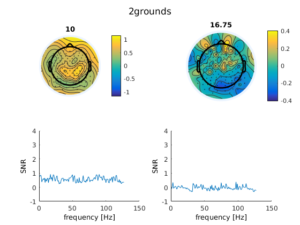
At first we thought, cool! ANT with active shielded cables is perfect, we will just not record with the brainproducts system. But ANT/tmsi allows to “chain” two amplifiers together to effectively get 127 electrodes. That is, the amplifiers share a ground electrode and a single electrode is bridged, so that the data can be referenced to a amplifier-common electrode. When we did this the following picture emerges:

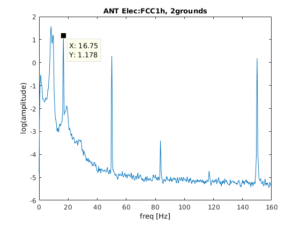
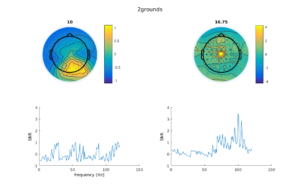
The 16 Hz is back! :(. The electrode depicted in the spectrum plot is from the second amplifier. In the lower right panel we can see, especially in the second plot, that the second amplifier has a lot of 16Hz artefact but not so much in the first amplifier.

ANT eegosport

We much later received an ANT eegosport for testing purposes. Unfortunately for us (and ANT because we did not upgrade ;)), the artefact was also present with comparable strength. Here an interesting new phenomenon arised: when flipping the amplifiers upside down, the artefact switched from channel 1-32 to 33-64 or vice versa.

Typical artefact behavior

The artefact was non-stationairy over time (sometimes its there, sometimes not, stronger, weaker …). Most often observed in the second amplifier, sometimes in the first. The artefact also was stronger (relatively) around the reference electrode. It does not depend on exact placement in room. We tried a lot of factors, at some point even wrapping things in foil – it did help a bit!

What the hell is going on?

Turns out, the new building is quite close to train tracks. In Northern Germany most trains are powered electrically using overhead lines. Germany uses $16 \frac{2}{3}$ Hz to power these lines. So sometimes when a train comes along we have an artefact. Because we did not want to time our experiments to the train schedule (we a) thought about it, but the DeutscheBahn does not give away information when trains are coming and b) the artefact is not _always_ strong when a train comes, but only sometimes, also not train dependent – but who knows…)

What can we do against it?

It took us the most part of the year (with lots of discussion with ANT & TMSI) to figure out, where exactly the artefact is induced into the signal.

Our solution

• Keep the cables as close together as possible, all in one orientation. Because the ANT REFA system allows the ~10cm cable to go into various direction, the common-noise which influences these channels can be slightly different. If the electrical field / artefact is strong enough, this slight differences will show up in your data. Thus always keep all cable very similar. We now “comb” the connector cables
• Keep the cables parallel to the field-lines of the electrical field. I.e. don’t put your cables parallel to the elongated electrical source, this will induce stronger effects. We now lead the cables to the top, so inline with the electric field
• If you use a cascaded system, the reference-electrode that links the two systems, has to follow both strings of electrodes. I.e. you have to guide it along the connector. If you fail to do so, there will be stronger artefact in one than in the other amplifier (depending on how the cable lays relative to the artefact electrical field). We now take care of this.

Combining all these measures helped us enourmously to reduce the artefact in a stationairy setting. For mobile recordings this will be tougher.

Debugging Lessons Learned

It took us a long time to figure out how to measure the artefact reliably and how to manipulate the system in order to study the artefact. Here are some lessons learned:

• A waterbucket+salt (=> a head without needing a human) is your friend. BUT: We tried this earlier and failed because the system was DC-maxing out (no signal in range). This was because we put in the whole ground electrode (which has a zink-connector) and not only the tip (AgCl). This gives very large DC offsets due to the zink contact and you cannot measure.
• Making turn around times super fast. This allows for more tests and easier replication of supposedly found effects. A online/live-script that shows us the current 16Hz power was very helpful here but took quite some programming to get smoothly.
• You need to show a lot of own initiative, support can help you, but not save you. This problem was very specific for us, a general solution did not exist
• If there is a non-stationairy noise source, it is very helpful to monitor the artefact with one amplifier while modifying things with the other amplifier. Only like that can you be sure that the artefact occured / your modification actually changed something (and you did not just measured in a low-artefact regime). An interesting phenomenon we saw, was that on one day after ~19.00 the artefact vanishes. We are not sure why this is the case, because trains were still running. The trains passing by do not produce a reliable effect in itself. We think this is because the power to the grid is turned on whenever a train is on the whole section, with a section being multiple kilometers long and possibly reaching into the trainstation (but we do not know this before).

Methods

We detrended or highpass filtered the data at 1Hz. Welchs estimate does not like DC-drifts. We generally either bandpass filter the data, or use the pwelch algorithm. We also employed the TMSI matlab-toolbox and programmed a live-script to monitor the 16Hz activity while manipulating the EEG. We also used some normalization to compare the signal to its frequency-bin neighbours. This allows for relative noise effects that show up when re-referencing to a single electrode.

I uploaded the tmsi EEG live-script on github

I showed a student how I would improve a plot. The result is I think typical for what I would design. The details change for each paper and I do not have a specific “style” I wanted to emulate. I usually enjoy the before & after of other graphics, so here is mine:

PS: The data shown in the plots are preliminary

We just published a new paper in the Journal of Vision

The temporal dynamics of eye movements as an exploitation-exploration dilemma
Ehinger Kaufhold & König, 2018

The highlights:

• We put eye movements as a decision process between exploitating the current view and exploring more of the scene
• We use gaze-contingent eye-tracking to control the When and Where of eye movements
• We find large effects of how long a subject fixates on their reaction time to continue exploring
• We find large effects of the number of possible future target locations (Hick’s effect)

Check out the paper at the Journal of Vision
doi:10.1167/18.3.6

Often when developing with psychotoolbox or psychopy/opensesame your program crashes. And I often then have a full-screen window open and cannot click somewhere else. I then try to Alt+Tab and execute “sca” (screen close all) into the matlab console, with often mixed success. Sometimes restarting the computer is the last option. Instead of restarting, a useful command in older ubuntu versions was: STRG + ALT + Backspace => restart X server (=> restart GUI).

In order to activate this again use:

setxkbmap -option terminate:ctrl_alt_bksp

source on askubuntu

PS: I wrote this blogpost because I looked up this thing multiple times – now I know where to look 😉

From time to time I explain concepts and ideas to my students.

Background

Often this pops up in a statistical context, when one has a non-linear dependency between the to-be-predicted variable and the predictor-variables. By transforming the predictors, relationships can be made linear, i.e. a logarithmic (exponential, quadratic etc.) relationships can be modeled by a **linear** model.

The idea

I have a very visual understanding on basis-functions / non-linear transformation of variables in terms of stretching / condensing the basis (the x-axis here). This can also be applied to the generalized linear model (here for logistic regression).

Imagine that the x-axis of a plot is made of some kind of elastic material, you can stretch and condense it. Of course you do not need to stretch every part equally, one example would be to stretch parts that are far away from zero, exponentially more than parts that are close to zero. If you would have an exponential relationship ($ y = e^x$) then $y$ would now lie on a straight line.

TLDR;

Imagine you have a non-linear relationship, by stretching the x-axis in accordance to that non-linear relationship, you will have a linear relationship.

An exemplary non-linear relationship:

We want to do $y = b_0 + b_1x $ but obviously a linear line does not fit well. We can do something called polynomial expansion, i.e. add more predictors which are simple transformations of the predictor $x$. i.e. $y = b_0 + b_1x + b_2x^2 + b_3x^3$

The trick comes here: We can interpret the new $x^3$ basis function as a stretching of the x-axis. I.e. the further we move out on the x-axis, the longer we need to stretch the parts (exactly by x^3 times)

This can be shown also for other functions:

Exponential

Logarithmic

Note that the logarithm is not defined for negative numbers

Quadratic

Note how the stretching can be negative, i.e. the original negative values are stretching/transformed to positive values

Using the trick on the y-axis

One can interprete **logistic regression** with the same trick:
$$ g{-1}(y) = b_0 + b_1*x <=> y = g(b_0+b_1x)$$
with $g$, the logistic (logit) function and $g^{-1}$ the inverse logistic function (invlogit)
$$ g^{-1} = \ln\frac{p}{1-p} <=> g = \frac{1}{1+e^{-x}}$$

Usually we would have some non-linear dependency on a probabilty of e.g. success. That means, with a low value of x, your success-chance are low. To model this kind of data, one can transform the y-axis using $g$ above.

Sometimes I need matlab/rstudio/spyder but with access to the university network. One way is to run matlab/rstudio/spyder on the university computers, but get the X (=Graphics) display on my local windows machine.

Because there is a gateway in between, I first need to tunnel the gateway to a university working computer, then use a second putty session to ssh right through the tunnel directly to the target computer.

These are the steps I need to do:

– Putty: ssh to gateway.university:22;  Go to SSH-Tunnel and put source-port: 2222 (this is your local port you gonna target the second session). destination: remote-pc-that-runs-matlab:22

– Putty again: ssh to localhost:2222 with X11 forward enabled and “xming” installed

and perfect (but sometimes slow) remote-X11-forwarding. For the future I want to check out rdb to remotely control the session. This could be a quite useful in many cases because my programs are usually running anyway 🙂