On the onsets of clusters: A replication of Rousselet 2023 / adding ClusterDepth
I recently read this paper, on the measurement of onsets of clusters in EEG data from Guillaume Rousselet and later got asked to be a reviewer of the paper. The main point it raises is a different one to what I adress in the paper: Most people do not explicitly test for an onset, they fall victim to the interaction-fallacy. In principle, you need an explicit test, testing e.g. timepoint 100 vs. 150 to check whether the activity changed significantly.
But because I recently implemented the ClusterDepth algorithm in Julia, I thought it would be nice to add this to the papers algorithms to test onsets (and I thought it should do great).
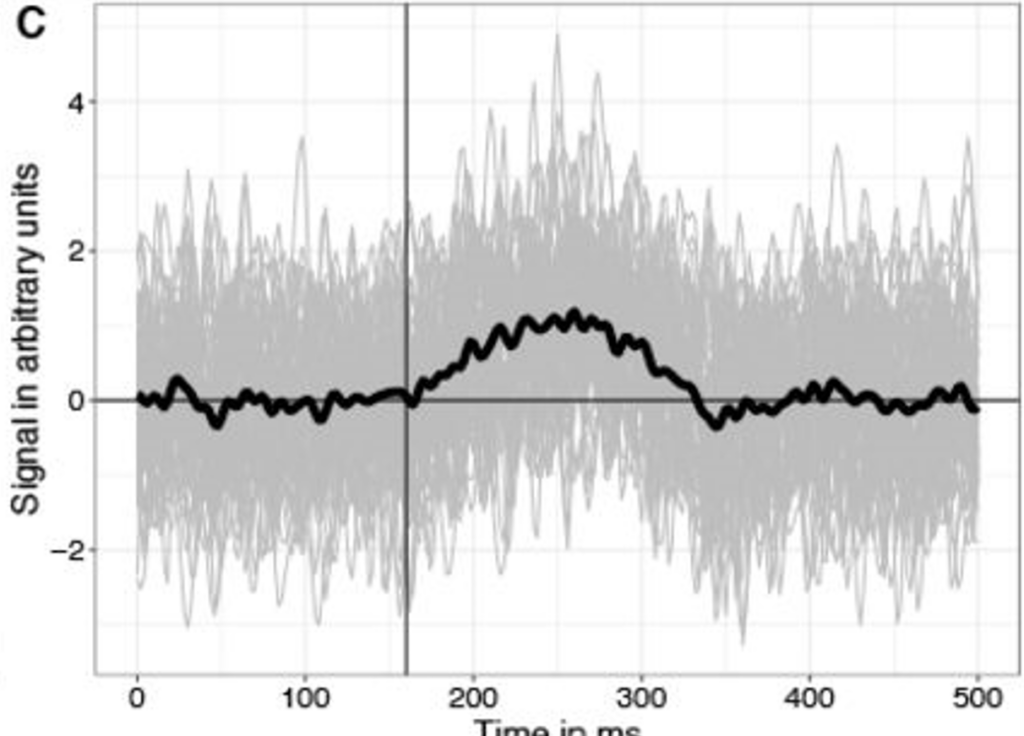
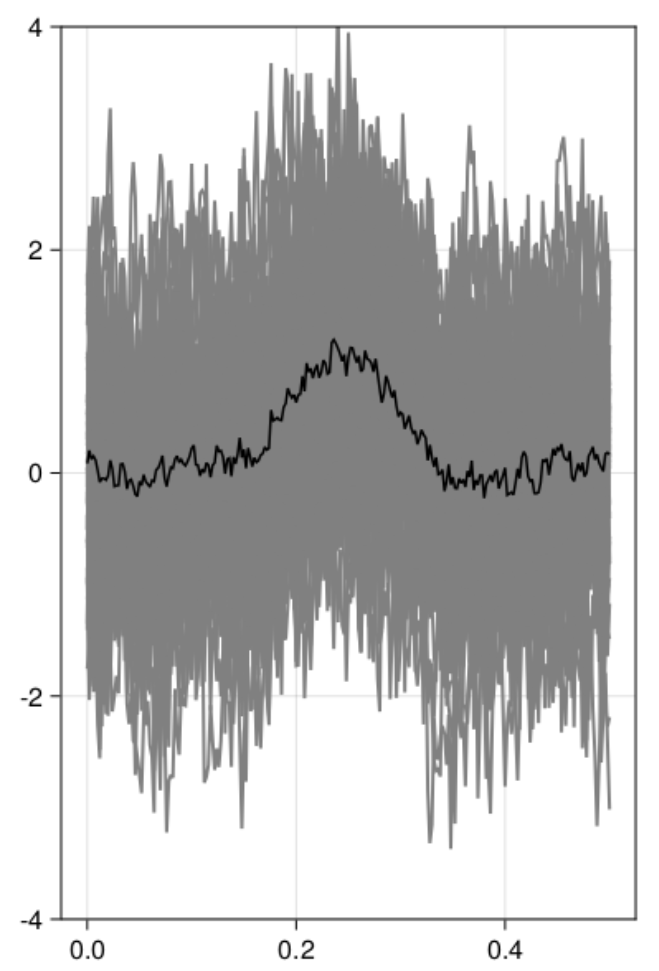
Let’s start with simulating data – I used our toolbox UnfoldSim.jl which made simulation relatively easy
design = SingleSubjectDesign(;conditions=Dict(:condA=>["noise","test"])) |> x->RepeatDesign(x,50);
signal = LinearModelComponent(;
basis=basis_signal,
formula = @formula(0~1+condA),
β = [0,1]
);
noise = PinkNoise(;noiselevel=1);
sim(seed) = simulate(MersenneTwister(seed), design, signal, UniformOnset(1,1), noise; return_epoched=true);Next, I ran clusterdepth a 100 times (the paper uses many more repetitions) using
cls = clusterdepth(d,statFun=ttest,permFun = permute_fun,nperm=2000)
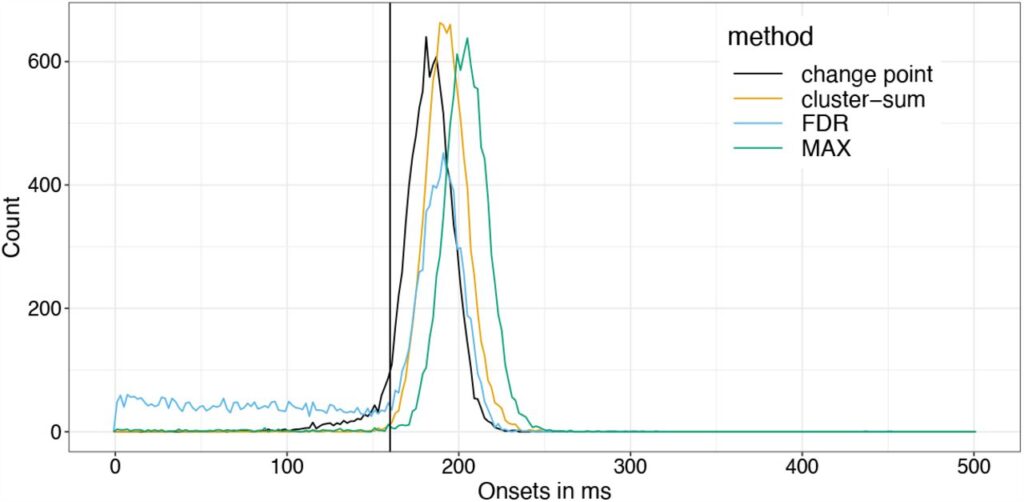
onsettimes.clusterdepth[k] = times[findfirst(<=(0.05),cls)]And plotted everything
As you can see, Cluster-sum is earliest, then FDR but with many false positives in the bsaaeline, and then maxT / clusterdepth. My implementation contains clusterdepth, but I did not implement the change-point detection. I think the results very nicely replicate Rousselet 2023!
I am surprised though, that the clusterdepth did not perform better, and I’m currently investigating why this is the case.

Hi Benedikt,
Thanks for the replication, that’s great to see similar results with a different implementation.
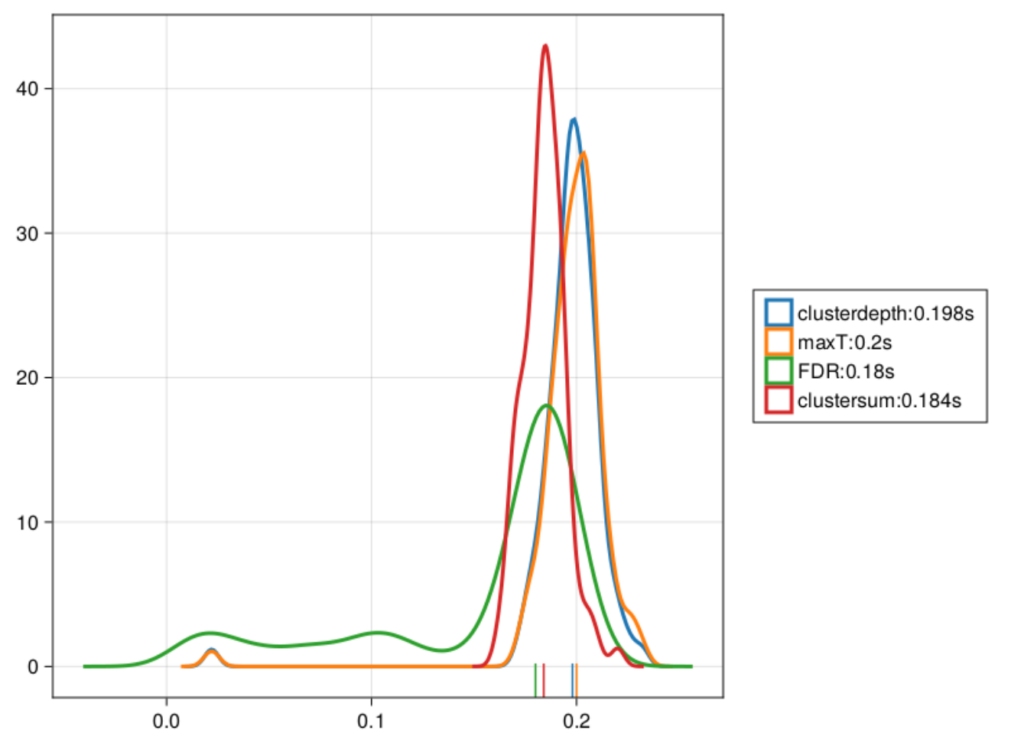
Using the cluster-depth code in the permuco R package, I now get very similar results to yours.
Unless I misunderstood something about the new cluster-depth approach, I think what’s going on is that even though each time point in the cluster is assessed using its own distribution based on its position, which should boost power, there is no lumping of points inside the cluster, so the weaker effects near the onset do not get the massive boost afforded by the cluster-mass statistics. Still need to check that in more detail. Is that your understanding of the algorithm as well?
great to hear the simulations are similar!
Indeed, there is no massive boost at the corners by design, but I expected a greater boost compared to tmax…