Matlab winsorized mean over all dimension

16. March 2016

This is a function I wrote back in 2014. I think it illustrates an advanced functionality in matlab that I hadn’t found written about before.

The problem:

Calculate the winsorized mean of a multidimensional matrix over an arbitrary dimension.

Winsorized Mean

The benefits of the winsorized mean can be seen here:

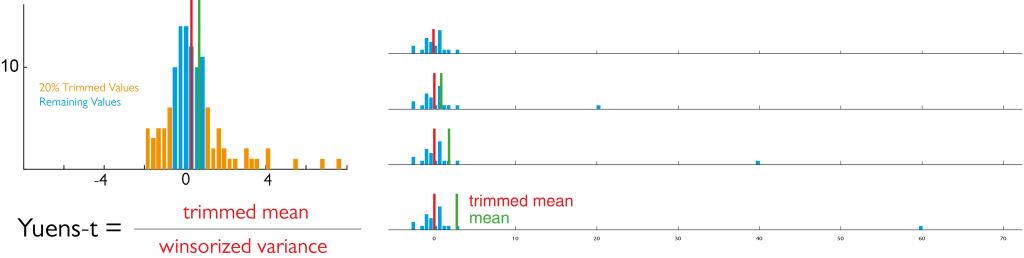
We replace the top 10% and bottom 10% by the remaining most extreme value before calculating the mean (left panel). The right panel shows how the mean is influenced by a single outlier, but the winsorized mean is not (ignore the “yuen”-box”)

Current Implementation

I adapted an implementation from the LIMO toolbox based on Original Code from Prof. patrick J Bennett, McMaster University. In this code the dimension is fixed at dim = 3, the third dimension.

They solve it in three steps:

sort the matrix along dimension 3
replace the upper and lower 10% by the remaining extreme value

calculate the mean over the sorted matrix

Generalisation

To generalize this to any dimension I have seen two previous solution that feels unsatisfied:
– Implement it for up to X dimension hardcoded and then use a switch-case to get the solution for the case.
– use permute to reorder the array and then go for the first dimension (which can be slow depending on the array)

Let’s solve it for X = 20 x 10 x 5 x 2 over the third dimension
[matlab]

function [x] = winMean(x,dim,percent)
% x = matrix of arbitrary dimension
% dim = dimension to calculate the winsorized mean over
% percent = default 20, how strong to winsorize

% How long is the matrix in our required dimension
n=size(x,dim);
% number of items to winsorize and trim
g=floor((percent/100)*n);
x=sort(x,dim);

[/matlab] up to here it my and the original version are very similar. The hardest part is to generalize the part, where the entries are overwritten without doing it in a loop.
We are now using the subsasgn command and subsref
We need to generate a structure that mimics the syntax of
[matlab] x(:,:,1:g+1,:) = y [/matlab] for arbitrary dimensions and we need to construct y

[matlab] % Prepare Structs
Srep.type = ‘()’;
S.type = ‘()’;

% replace the left hand side
nDim = length(size(x));

beforeColons = num2cell(repmat(‘:’,dim-1,1));
afterColons = num2cell(repmat(‘:’,nDim-dim,1));
Srep.subs = {beforeColons{:} [g+1] afterColons{:}};
S.subs = {beforeColons{:} [1:g+1] afterColons{:}};
x = subsasgn(x,S,repmat(subsref(x,Srep),[ones(1,dim-1) g+1 ones(1,nDim-dim)])); % general case
[/matlab] The output of Srep is:

Srep =
type: ‘()’
subs: {‘:’ ‘:’ [2] ‘:’ }

thus subsref(x,Srep) outputs what x(:,:,2,:) would output. And then we need to repmat it, to fit the number of elements we replace by the winsorizing method.

This is put into subsasgn, where the S here is :

Srep =
type: ‘()’
subs: {‘:’ ‘:’ [1 2] ‘:’ }

Thus equivalent to x(:,:,[1 2],:).
The evaluated structure then is:
[matlab] x(:,:,[1:2]) = repmat(x[:,:,1],[1 1 2 1]) [/matlab]

The upper percentile is replaced analogous:
[matlab] % replace the right hand side
Srep.subs = {beforeColons{:} [n-g] afterColons{:}};
S.subs = {beforeColons{:} [n-g:size(x,dim)] afterColons{:}};

x = subsasgn(x,S,repmat(subsref(x,Srep),[ones(1,dim-1) g+1 ones(1,nDim-dim)])); % general case

[/matlab]

And in the end we can take the mean, var, nanmean or whatever we need:
[matlab] x = squeeze(nanmean(x,dim));
[/matlab]

That finishes the implementation.

Timing

But how about speed? I thus generated a random matrix of 200 x 10000 x 5 and measured the timing (n=100 runs) of the original limo implementation and mine:

algorithm	timing (95% bootstraped CI of mean)
limo_winmean	185 – 188 ms
my_winmean	202 – 203ms
limo_winmean otherDimension than 3	218 – 228 ms

For the last comparison I permuted the array prior to calculating the winsorized mean, thus the overhead. In my experience, the overhead is greater the larger the arrays are (I’m talking about 5-10GB matrices here).

Conclusion

My generalization seems to work fine. As expected it is slower than the hardcoded version. But it is faster than permuting the whole array.