Comparing Manual and Atlas-based retinotopies; my journey through fmri-surface-land

PS: For this project I moved from EEG to fMRI, and in this post I will sometimes explain terms that might be very basic to fMRI people, but maybe not for EEG people.

I want to investigate cortical area V1. But I don’t want to spend time on retinotopy during my recording session. Thus I looked a bit into automatic methods to estimate it from segmented (segment = split up in WhiteMatter/GrayMatter+extract 3D-surfaces from voxel-MRI and also inflate them) brains. I used the freesurfer/label/lh.V1 labels and the neurophythy/Benson et al tools . The manual retinotopy was performed by Sam Lawrence using MrVista. And here the trouble begins:

The manual retinotopy was available only as a volume (voxel-file, maybe due to my completly lacking mrVista skills. I should look into whether I can extract the mrVista mesh-files somehow), while the other outputs I have as freesurfer vertex values, ready to be plotted against the different surfaces freesurfer calculated (e.g. white matter, pial (gray matter), inflated). Thus I had to map the volume to surface. Sounds easy – something that is straight forward – or so I thought.

After a lot of trial&error and bugging colleagues at the Donders, I settled for the nipype call to mri_vol2surf from freesurfer. But it took me a long time to figure out what the options actually mean. This answer by Doug Greve was helpful (the answer is 12 years old, nobody added it to the help :() (see also this answer):

It should be in the help (reprinted below). Smaller delta is better
but takes longer. With big functional voxels, I would not agonize too
much over making delta real small as you'll just hit the same voxel
multiple times. .25 is probably sufficient.

doug

   --projfrac-avg min max delta
   --projdist-avg min max delta

     Same idea as --projfrac and --projdist, but sample at each of the
     points    between min and max at a spacing of delta. The samples are then
     averaged    together. The idea here is to average along the normal.

The problem is that you have to map each vertex to a voxel. So in this approach you take the normal vector of the surface (e.g. from white matter surface), check where it hits the gray matter, sample ‘delta’ steps between WM (min) and GM (max), and check which voxels are closest to these steps. The average value of the voxels is then assigned to this vertex.

I will first show a ‘successful subject before I dive into some troubles along the way.

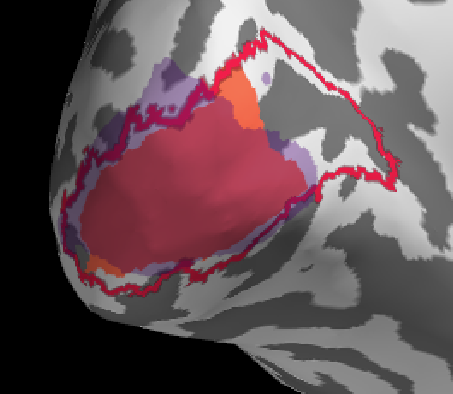
Overall a good match I would say, generally benson & freesurfer have a good alignment (reasonable), the manual retinotopy is larger in most subjects. This might also be due to the projection method (see below)

Initially I tried projection withour smoothing, see the results below. I then changed to a smooth of 5mm kernel with subsequent thresholding (for sure there is probably a smarter way).

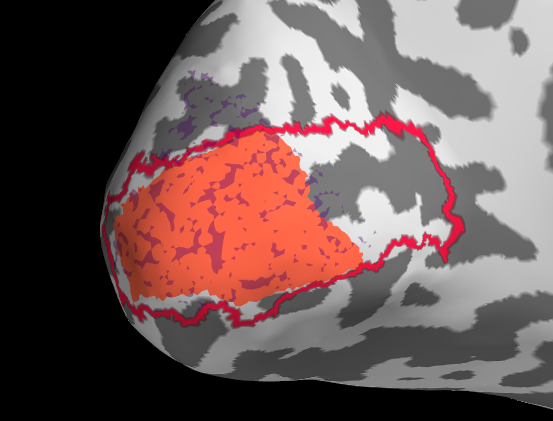
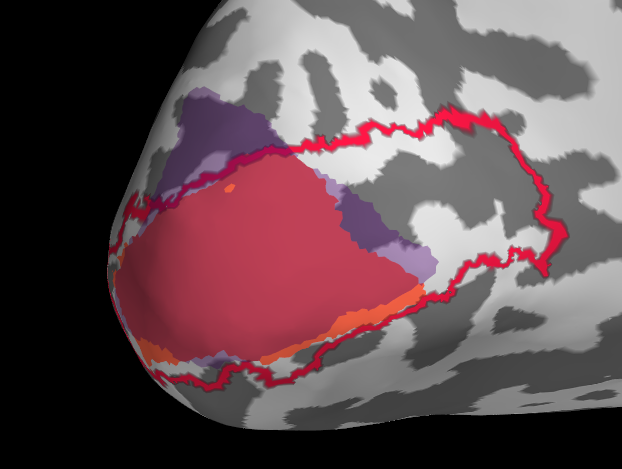
It is pretty clear that in this example the fit of manual with automatic tools is not very good. My trouble is now that I don’t know if this is because of actual difference or because of the projection.

Next steps would be to double check everything in voxel land, i.e. project the surface-labels back to voxels and investigate the voxel-by-voxel ROIs.