Applied Generalized Linear (Mixed) Modelling
Benedikt Ehinger
March 19th, 2018
Slides & my Presentation style
Click this link to add notes to the slides
this adds ?showNotes=true to the file
You can download the pdf or print them yourself:
click this link for pdf printable (use google chrome)
click this link for pdf printable + notes
HTML is best viewed in chrome
Organization
- 09.00 - 10.00 Lecture I
- 10.00 - 10.30 Q/A + break
- 10.30 - 11.30 Lecture II
- 11.30 - 12.00 Q/A
- 12.00 - 13.00 Mensa
- 13.00 - ~14.00 Lecture III / recap of yesterday’s exercises
- ~ 14.30 - ~18.00 Exercises in R and we offer help doing the exercises @ Gebäude 50!
Exam
Too many people for oral exam
=> Exam in 3-4 Weeks (date to be determined)
Scope: Content of course. Exercises are just to enhance your understanding (they are for you! Come and enjoy :-)).
No need to write R-Code in the course, you should be able to navigate R-Output (e.g. model output).
Athena: https://athena.cogsci.uos.de/
Please fill in the feedback after the second session
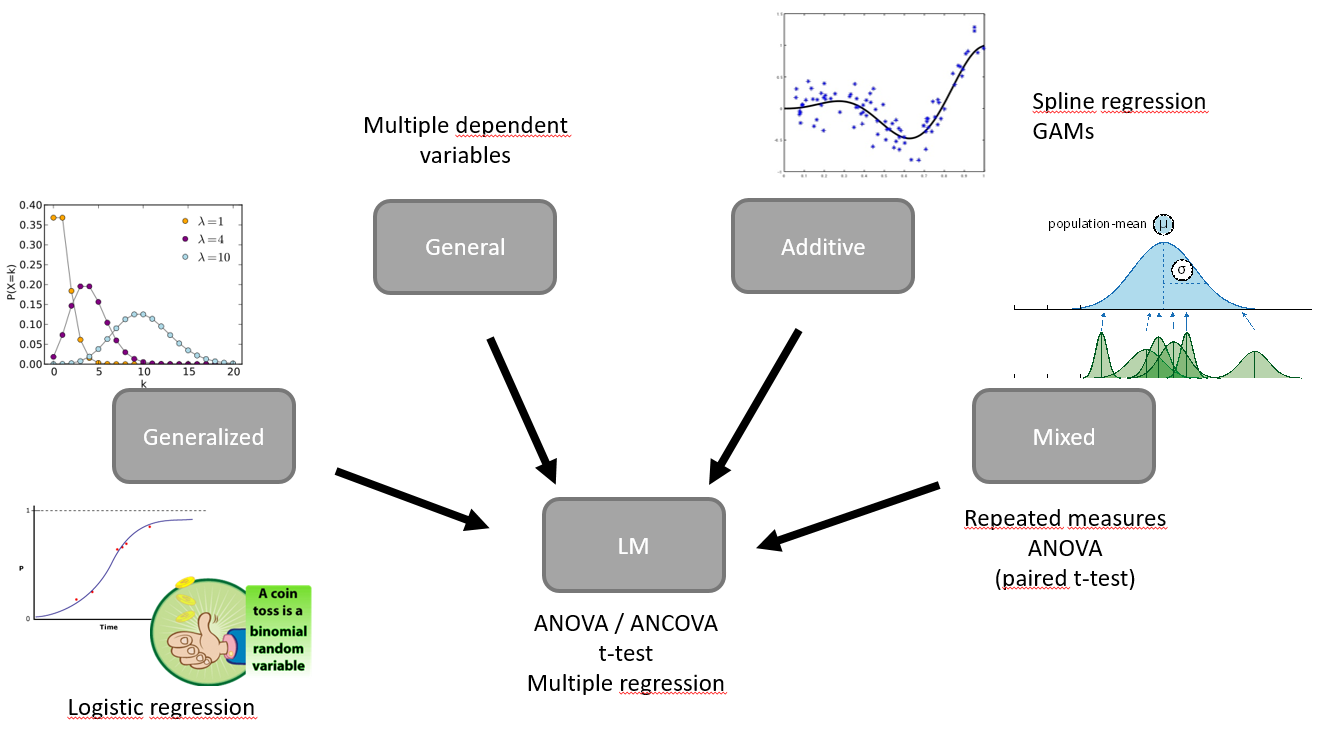
Course Overview
- Day 1: There is just one statistical test, linear regression, multiple regression, 2x2 design
- Day 2: Inference, Assumptions, Philosophy, t-test+ANOVA+ANCOVA
- Day 3: Logistic Regression, GLM
- Day 4: Mixed Models
- Day 5: Leftovers
Course Overview
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
Purpose of statistics
- Organization

- Description
- Inference
Why statistics in the first place?
Because of Variation

Most important lesson
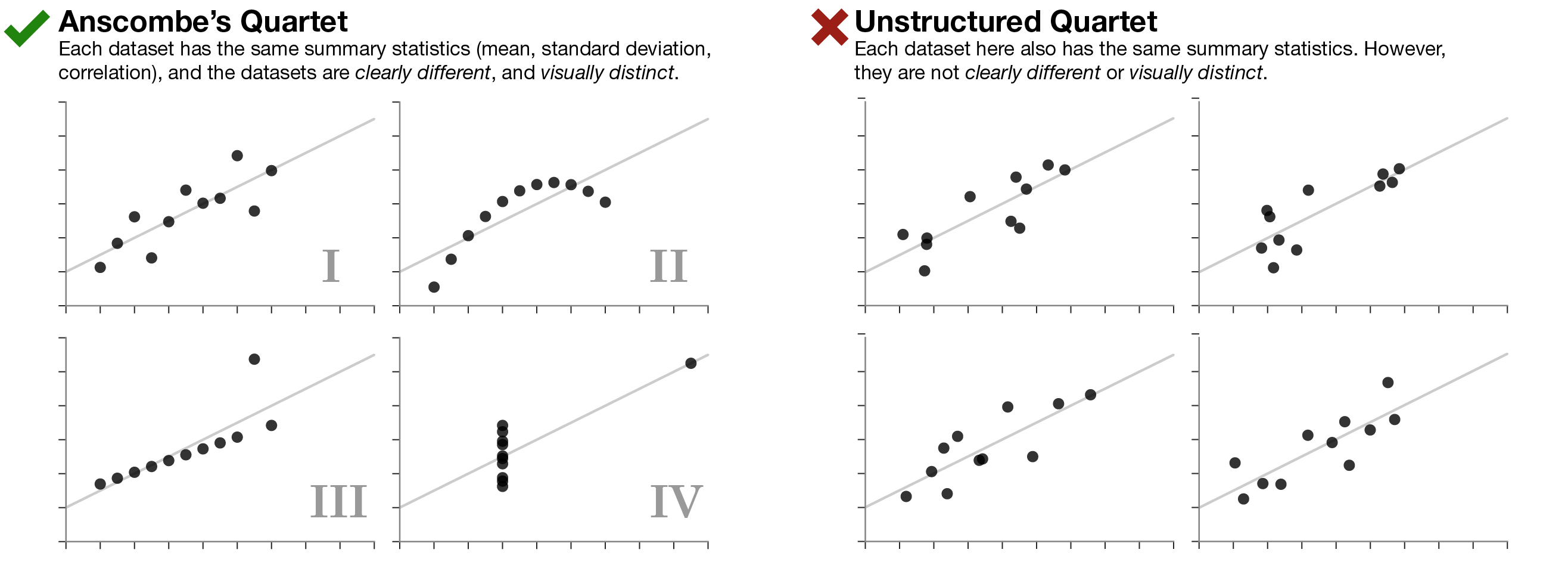
Always visualize your data
…make both calculations and graphs. Both sorts of output should be studied; each will contribute to understanding. F. J. Anscombe, 1973

Overview
- Warmup
- Why statistics
- do it yourself statistics
- three important concepts
- there is only one statistical test
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
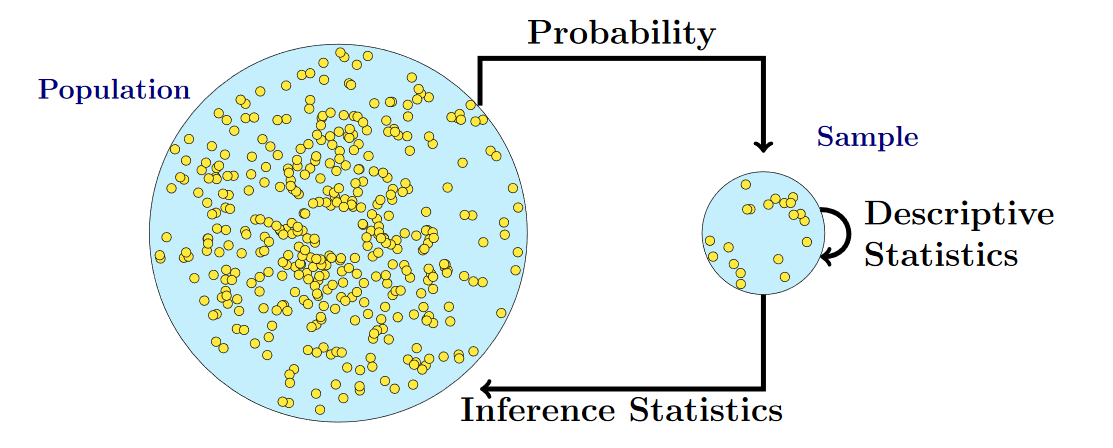
Three extremely important concepts
- Population
- Sample
- Sampling Distribution
Population
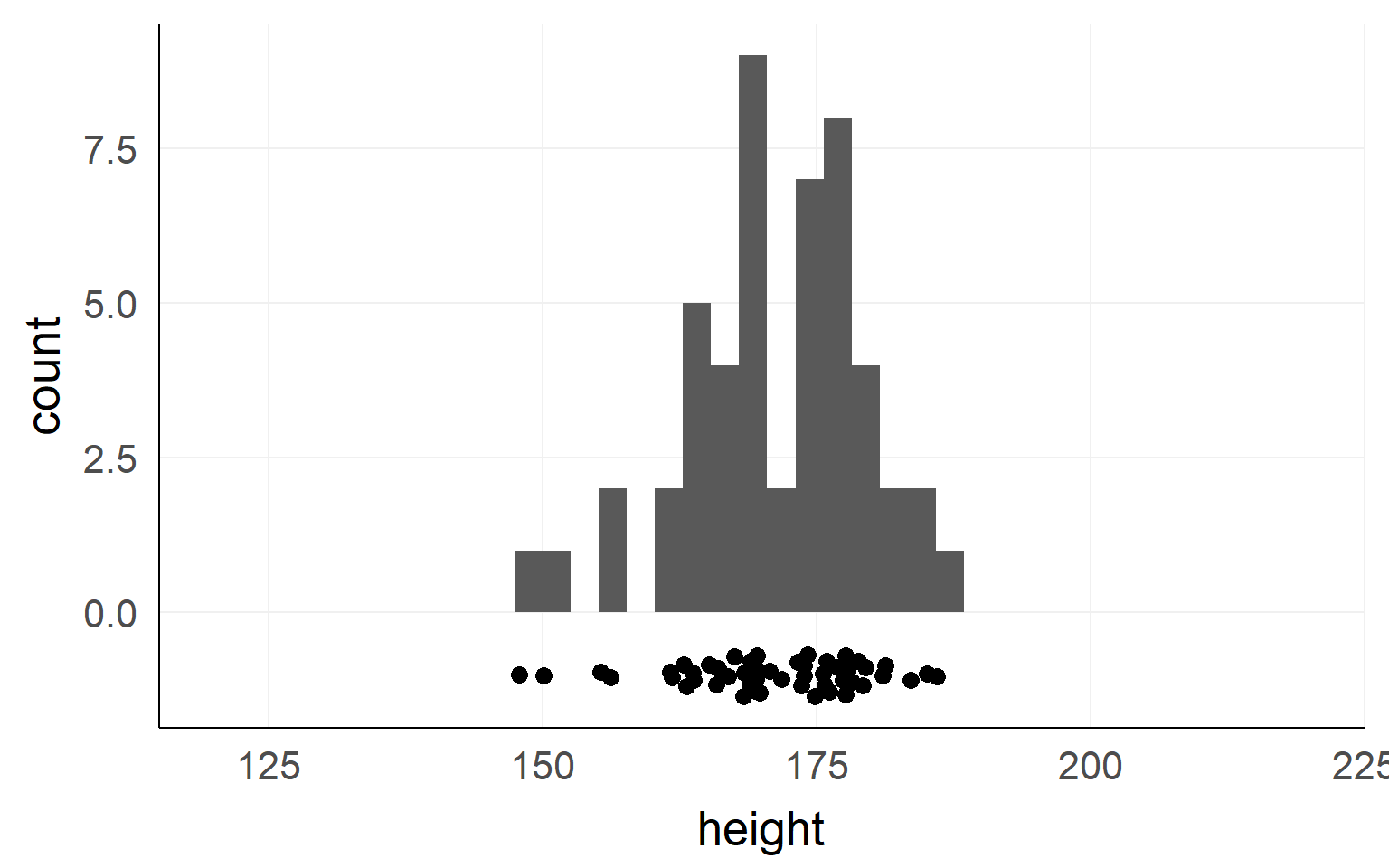
This could be the height of the population
of all people in this room.
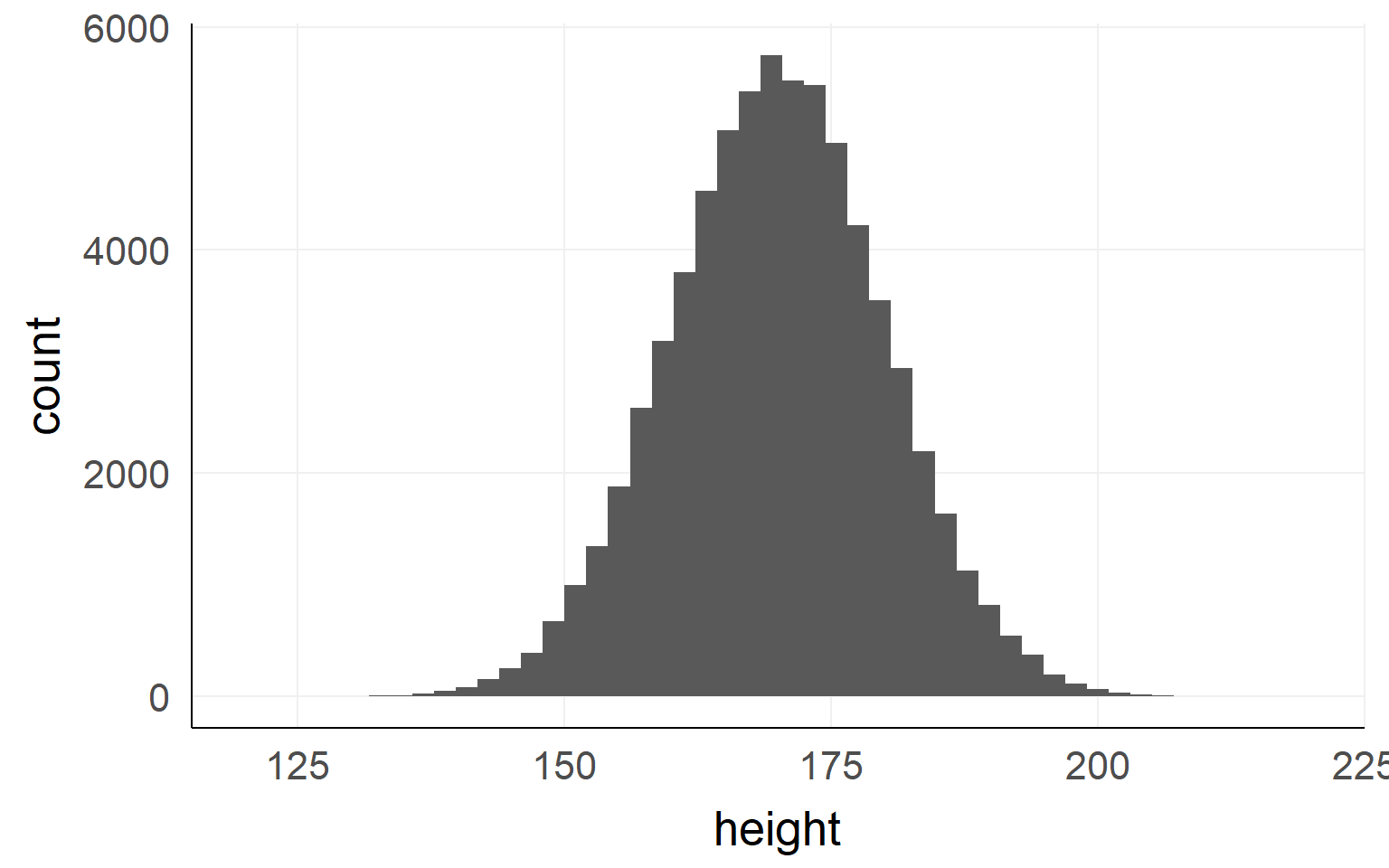
This could be the height of the population of all people in the world. The upper example is a sub-population.
Sample
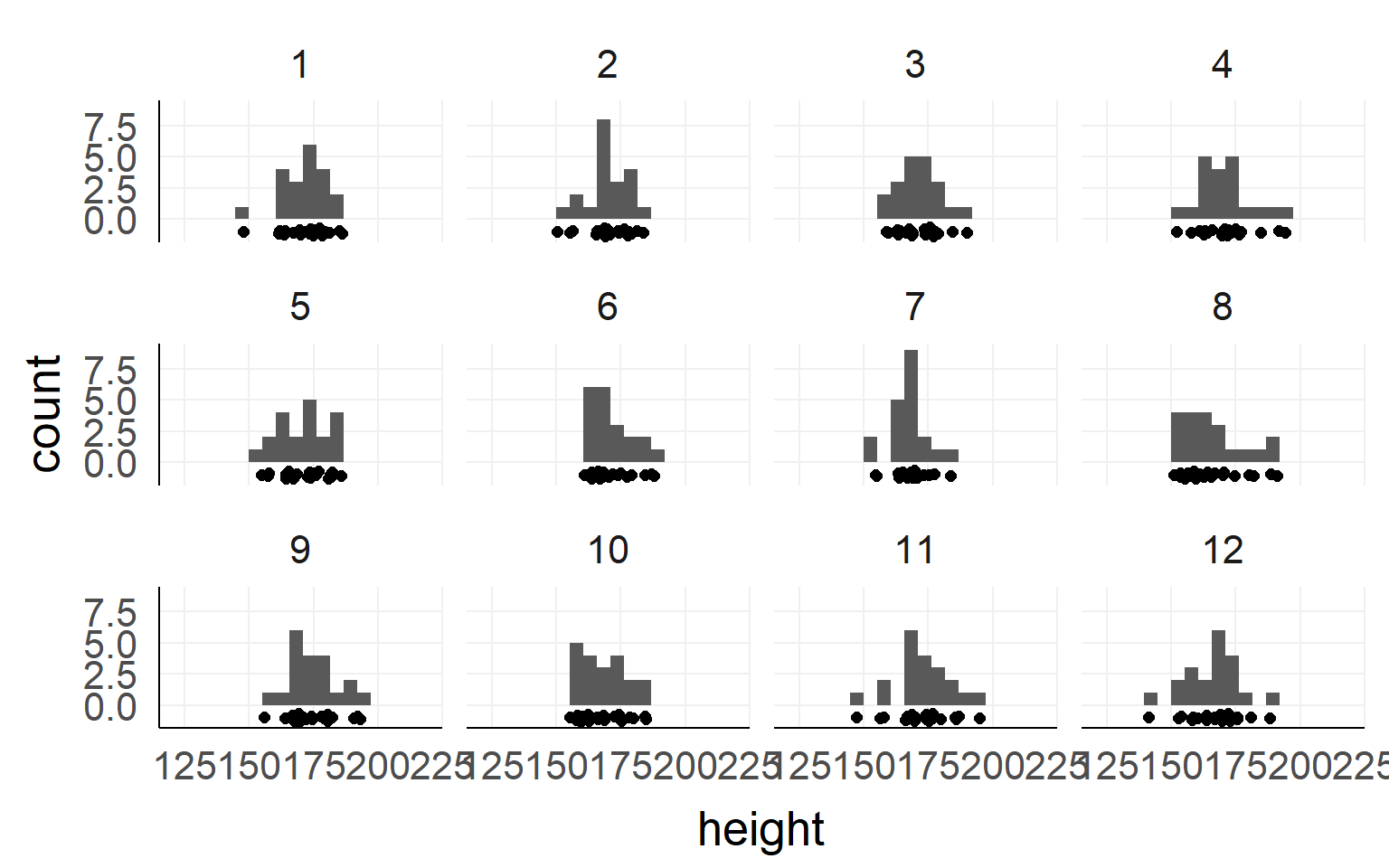
Height measured of 12 different samples (=experiment) of a population.
Sampling Distribution
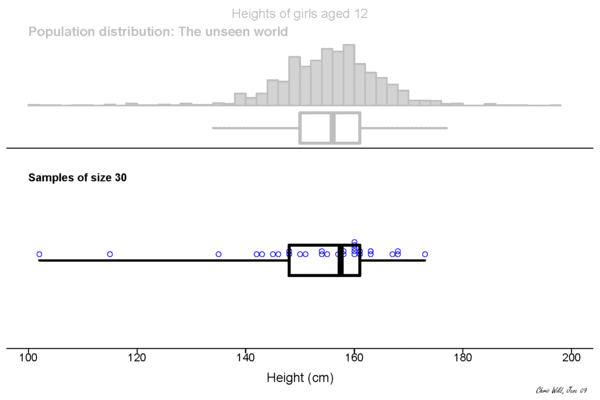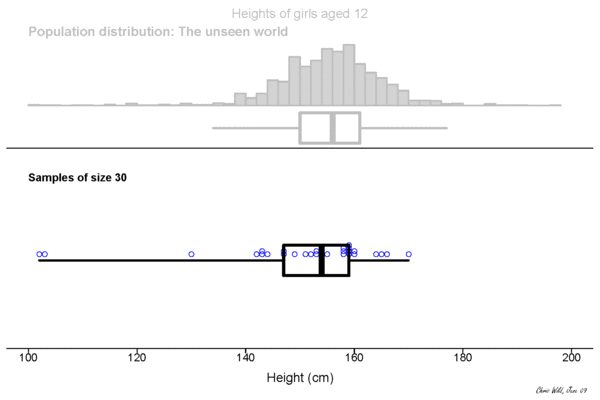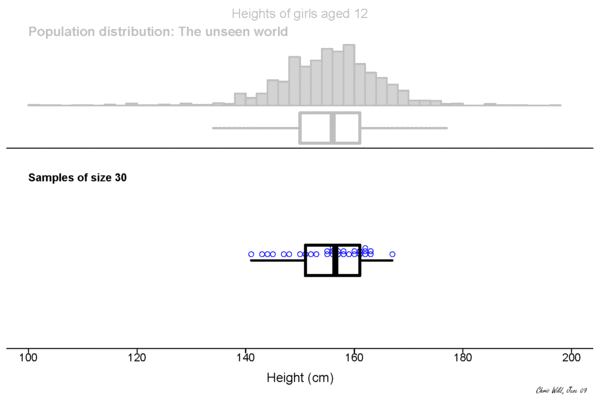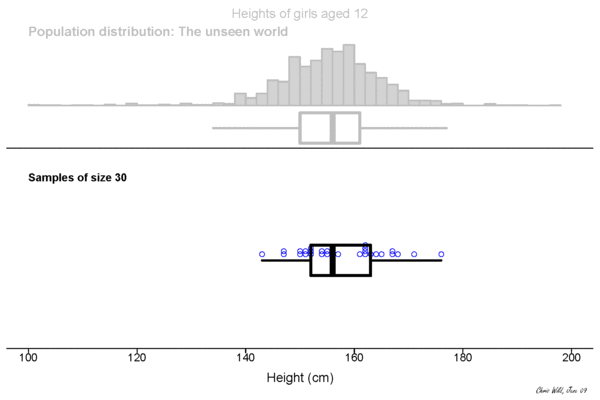
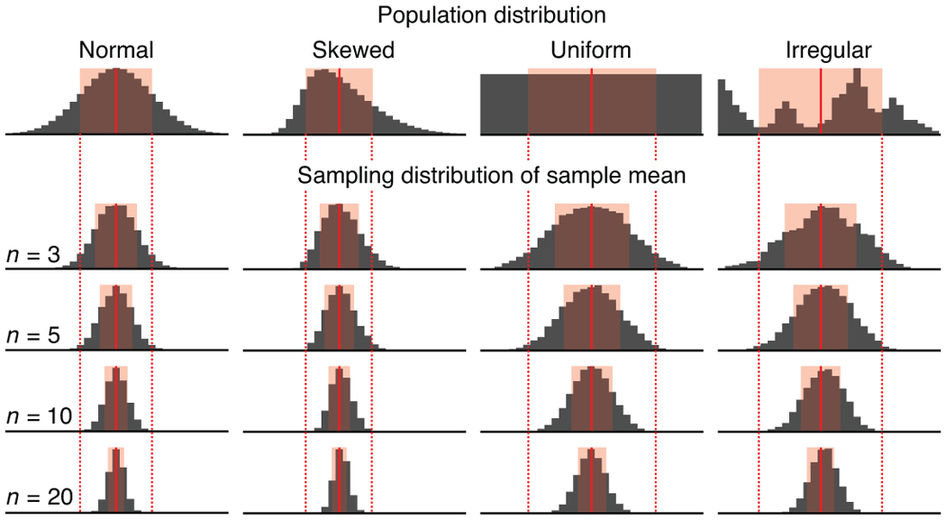
Central limit theorem
Overview
- Warmup
- Why statistics
- do it yourself statistics
- three important concepts
- there is only one statistical test
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
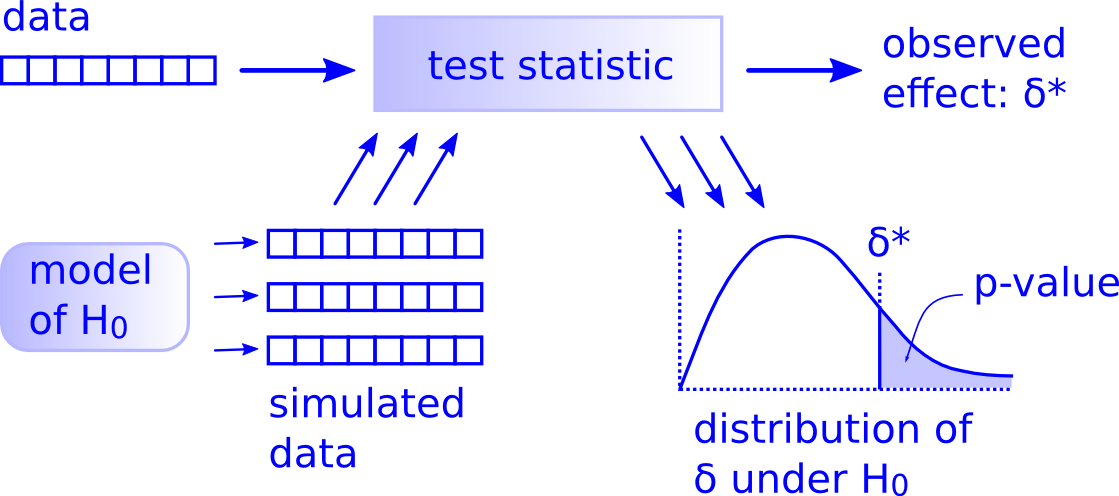
What are statistical inferences?
Ingredients for every statistical test
Q:Did our statistic\(^{*}\) occur due to chance\(^{**}\)?
A: To find out, look at the distribution of the statistic at the chance level!
\(^{*}\) could be any measure (statistic), usually: mean, median, variance, t-statistic etc.
\(^{**}\) chance-level is defined by the \(H_0\) (Null Hypothesis), most often it is mean = 0
Example \(n_{obs} = 10\)
## [1] -0.37645381 0.43364332 -0.58562861 1.84528080 0.57950777
## [6] -0.57046838 0.73742905 0.98832471 0.82578135 -0.05538839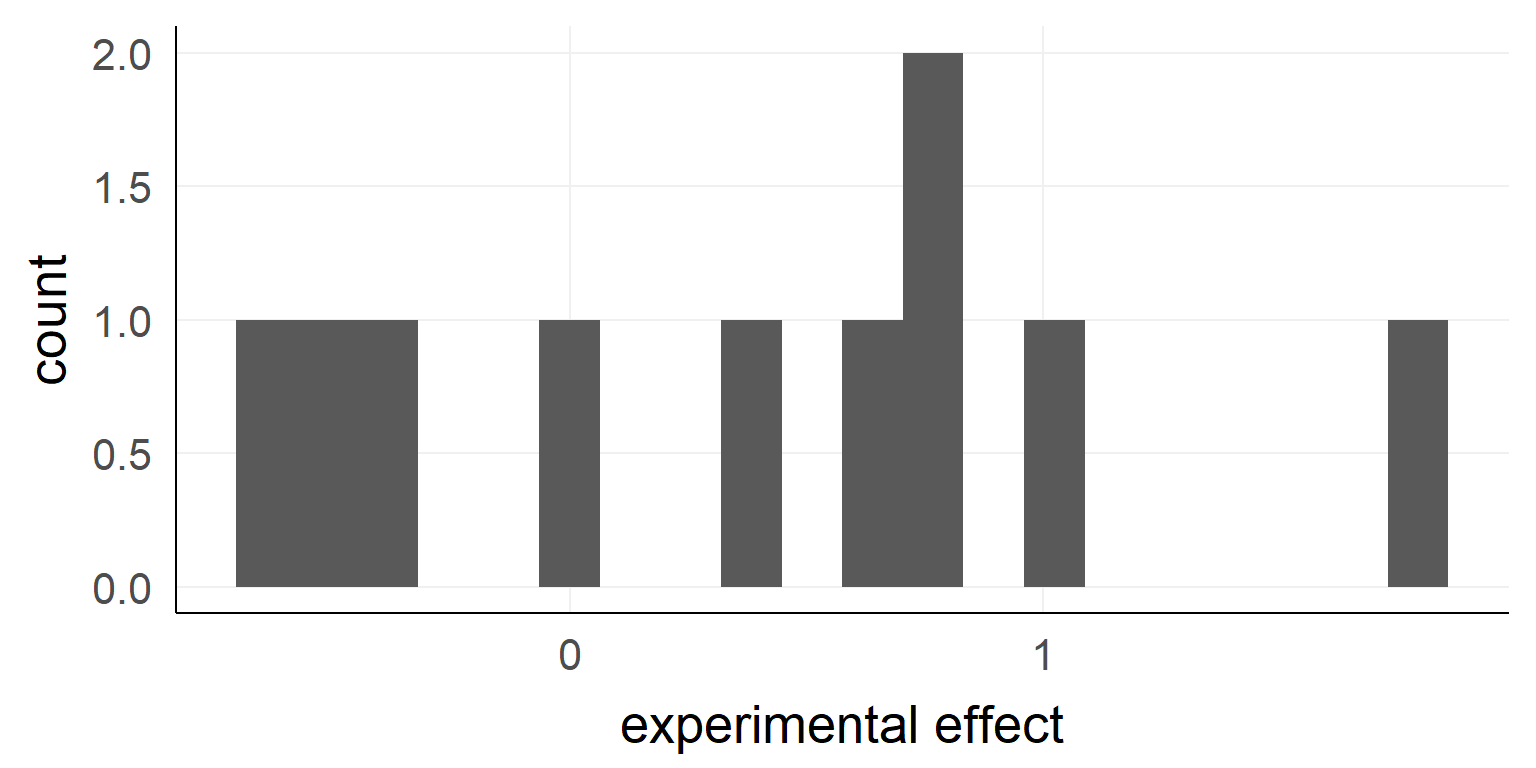
## [1] "mean:0.38, sd:0.78"What we need for our example:
- test-statistic:
- Let’s take the mean value for simplicity (mean(experimental effect) = \(\hat \mu\) = 0.38)
- Chance-Model (commonly called: model of \(H_0\)) - could (in principle) be anything. Let’s assume a normal distribution with a mean of 0 and standard deviation (\(\sigma) = 1\).
The \(H_0\) model
Take 1000 random samples with \(n = n_{obs} = 10\) each
dnull =replicate(1000, rnorm(10) ) %>%reshape2::melt()
null_stat = dnull%>%group_by(Var2)%>%summarise(m = mean(value)) # var2 codes the sample-ID
qplot(null_stat$m,bins=50)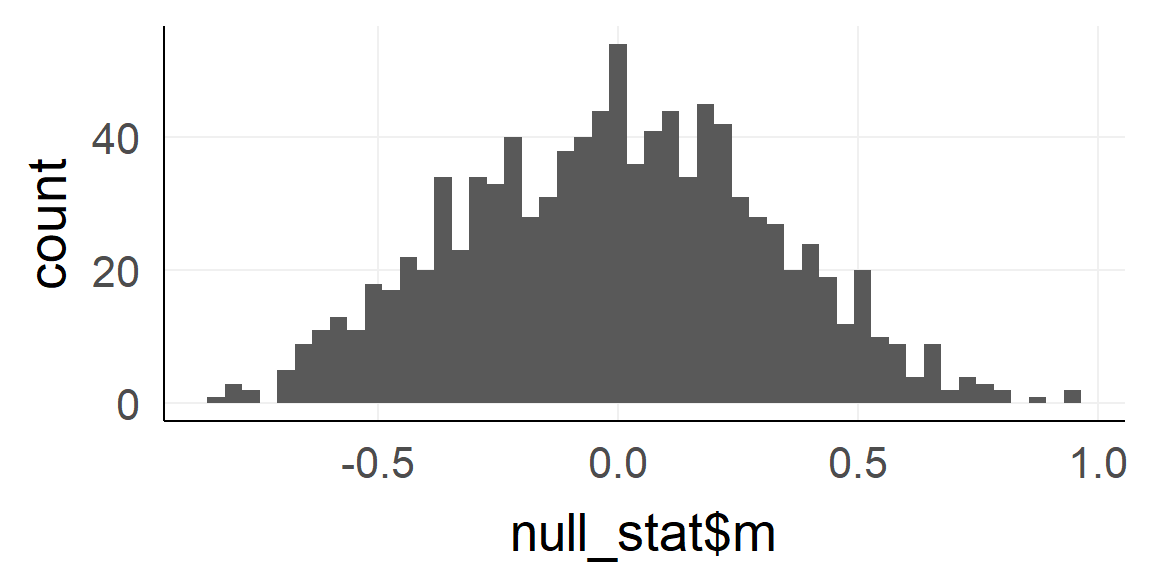
Q: What is this distribution called?
The p-value
Because standardization makes things comparable!
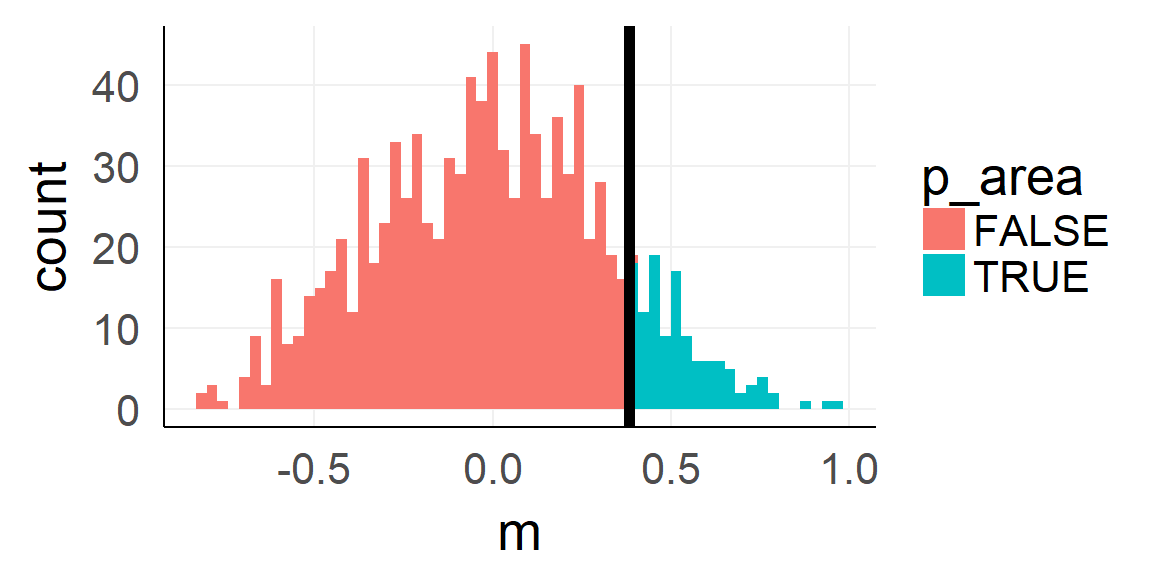
sprintf('p-value: %.3f',sum(null_stat$m >=mean(dobs)) / 1000)## [1] "p-value: 0.121"Analytic shortcut
Simulation can be expensive (e.g. in very complex models => day 4) and computers are needed.

For normal distributed populations (assumption!) the sampling distribution can be easily calculated (a normal with mean = \(mean_{H_0}\), \(SE = \frac{\sigma_{H_0}}{\sqrt N}\), Standard-error)
Summary
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Introducing the example
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
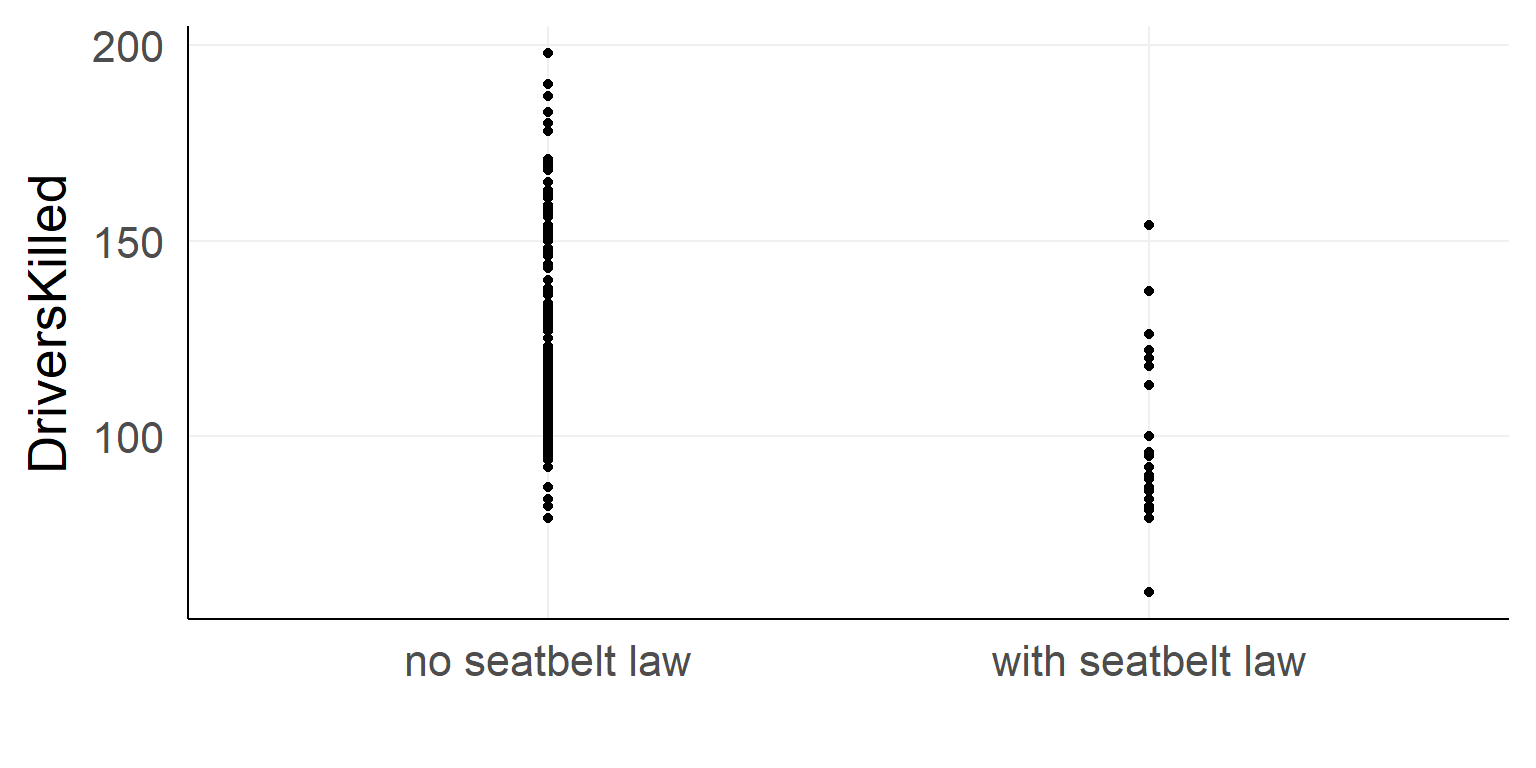
Should the seatbelt law be withdrawn?

ggplot(data,aes(x=law,y=DriversKilled))+stat_summary()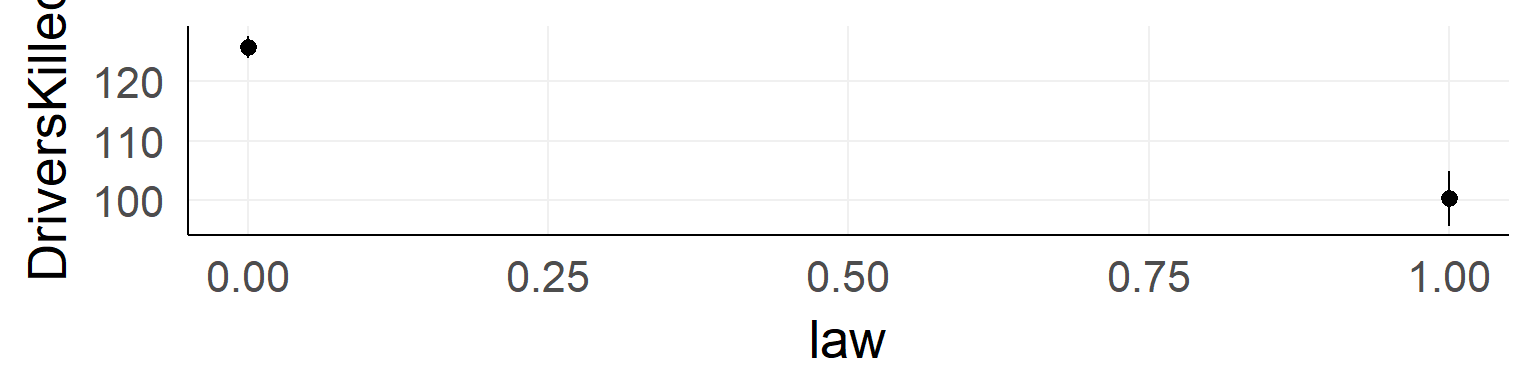
There could be confounds!
ggplot(data,aes(x=date,y=PetrolPrice,color=factor(law)))+geom_point()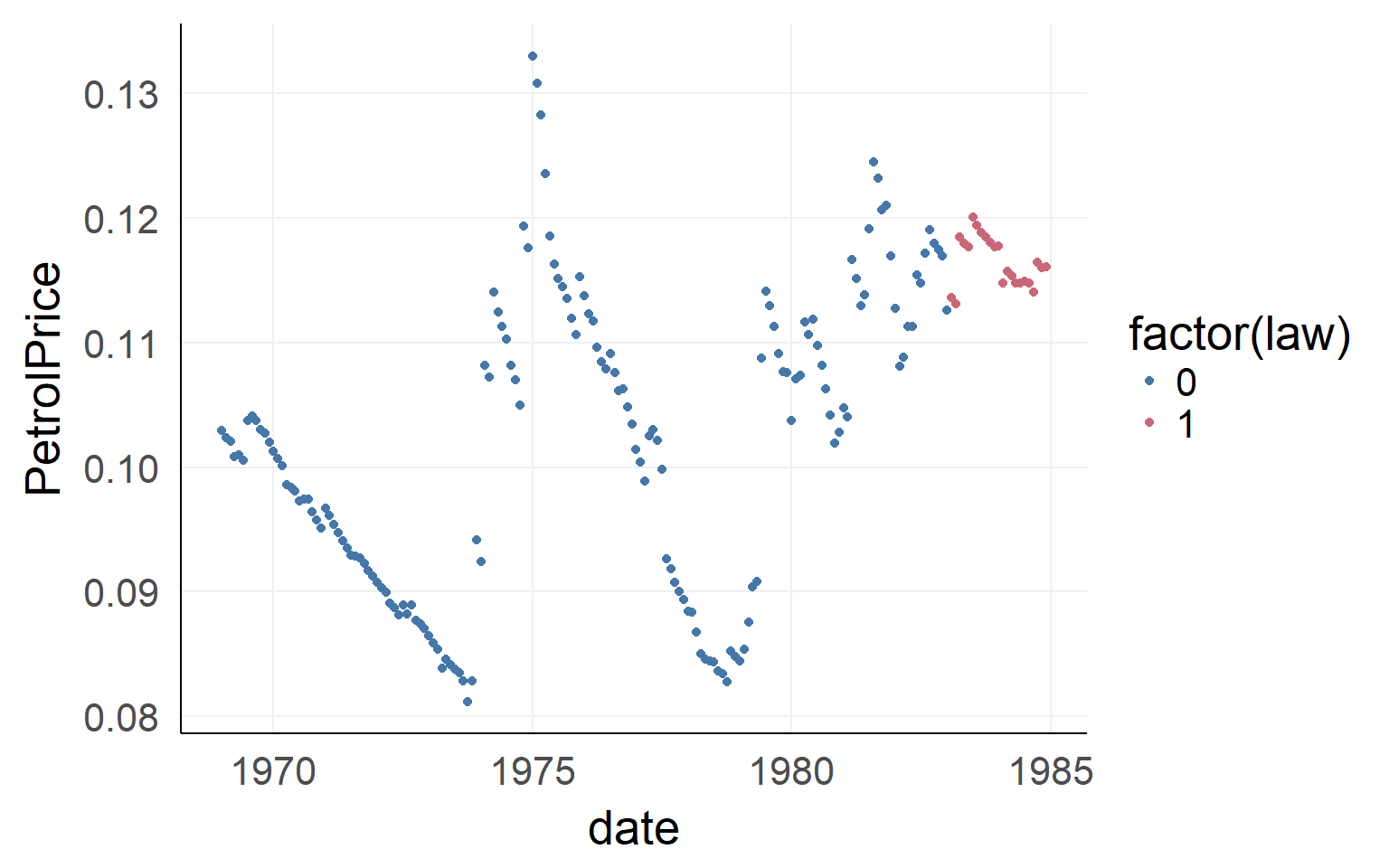 We will ignore the dependency in time. Please never do this in your data - this is an example only! You have been warned
We will ignore the dependency in time. Please never do this in your data - this is an example only! You have been warned
Preview: Multiple regression to the rescue
\(DriversKilled = Average+ kmDrivenEffect + TotalDriverEffect +\) \(PetrolPriceEffect + SeatbeltLawEffect\)
\(DriversKilled = \beta_{average} + \beta_1 \cdot kmsDriven + \beta_2 \cdot TotalDrivers +\) \(\beta_3 \cdot PetrolPrice + \beta_4 \cdot SeatbeltLaw + e_i\)
- Linear Models allow to structure and separate effects
- Linear Models allow to predict values (e.g. what if PetrolPrice would be double the size?)
- Linear Models can be easily extended for non-linear effects (e.g. GAM), complicated distributions(e.g. Yes/No aka logistic regression) or multiple outcomes (General Linear Model)
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
The simple linear regression
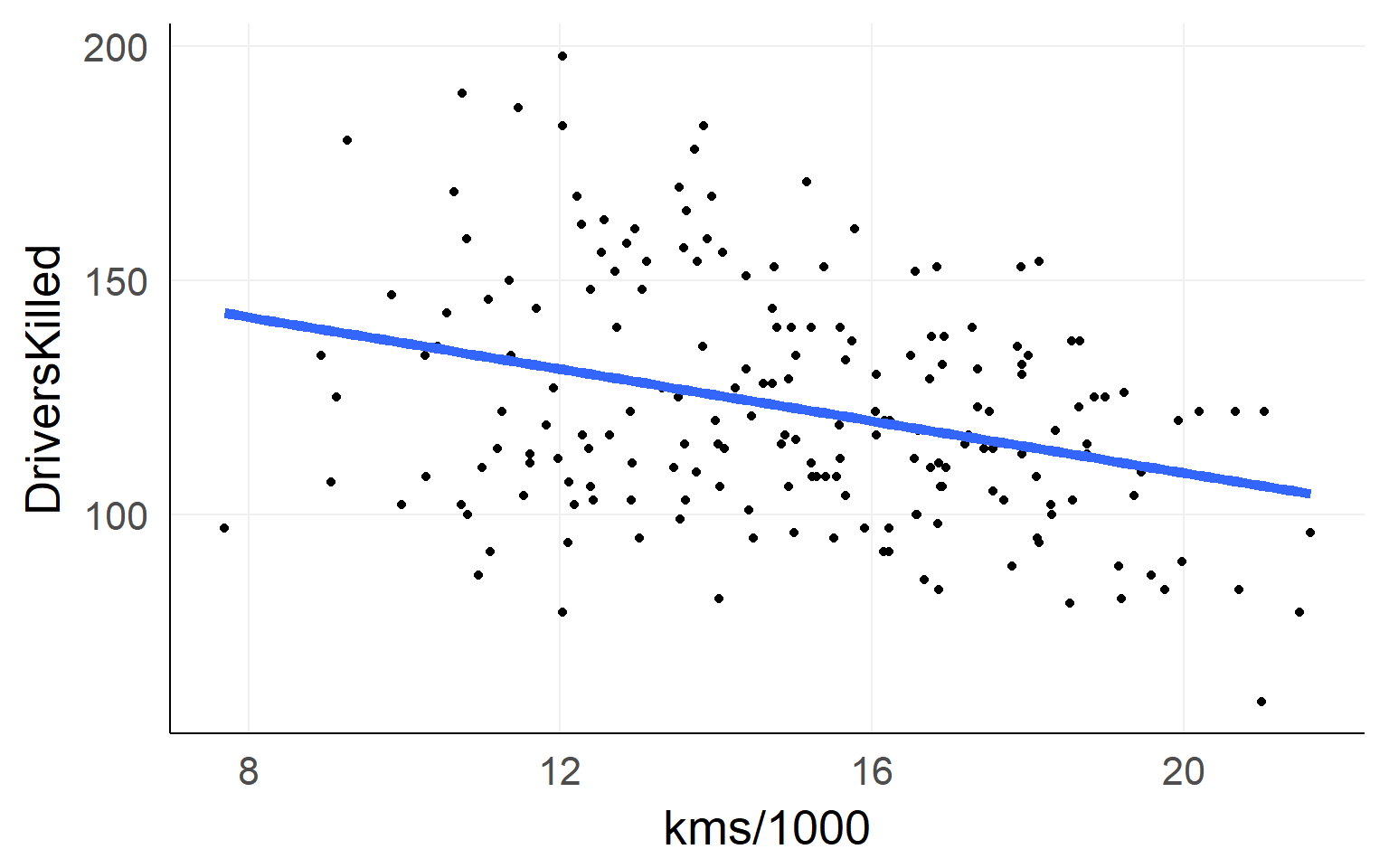
fit = lm(DriversKilled~1+kms,data)Lines are simple! Intercept + Slope
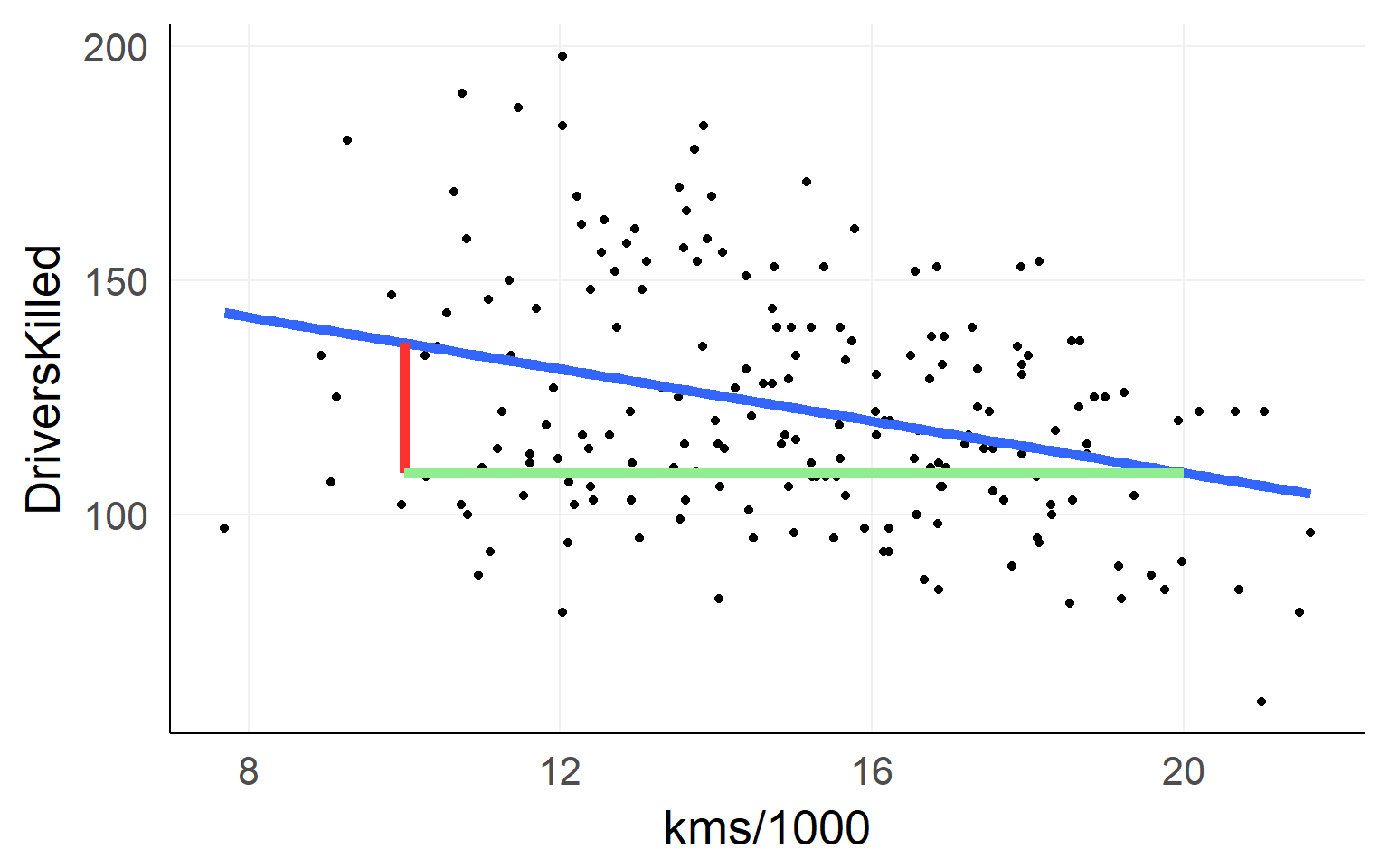
\[ DriversKilled = \beta_0 + (kms/1000) * \beta_1 \]
Red Line: \([DriversKilled | kms/1000==20] - [DriversKilled | kms/1000==10]\)
\(=\beta_0 + 20\beta_1 - (\beta_0 + 10\beta_1)\) \(=10\beta_1\)
Which line to choose?
Residuals / L2 Norm
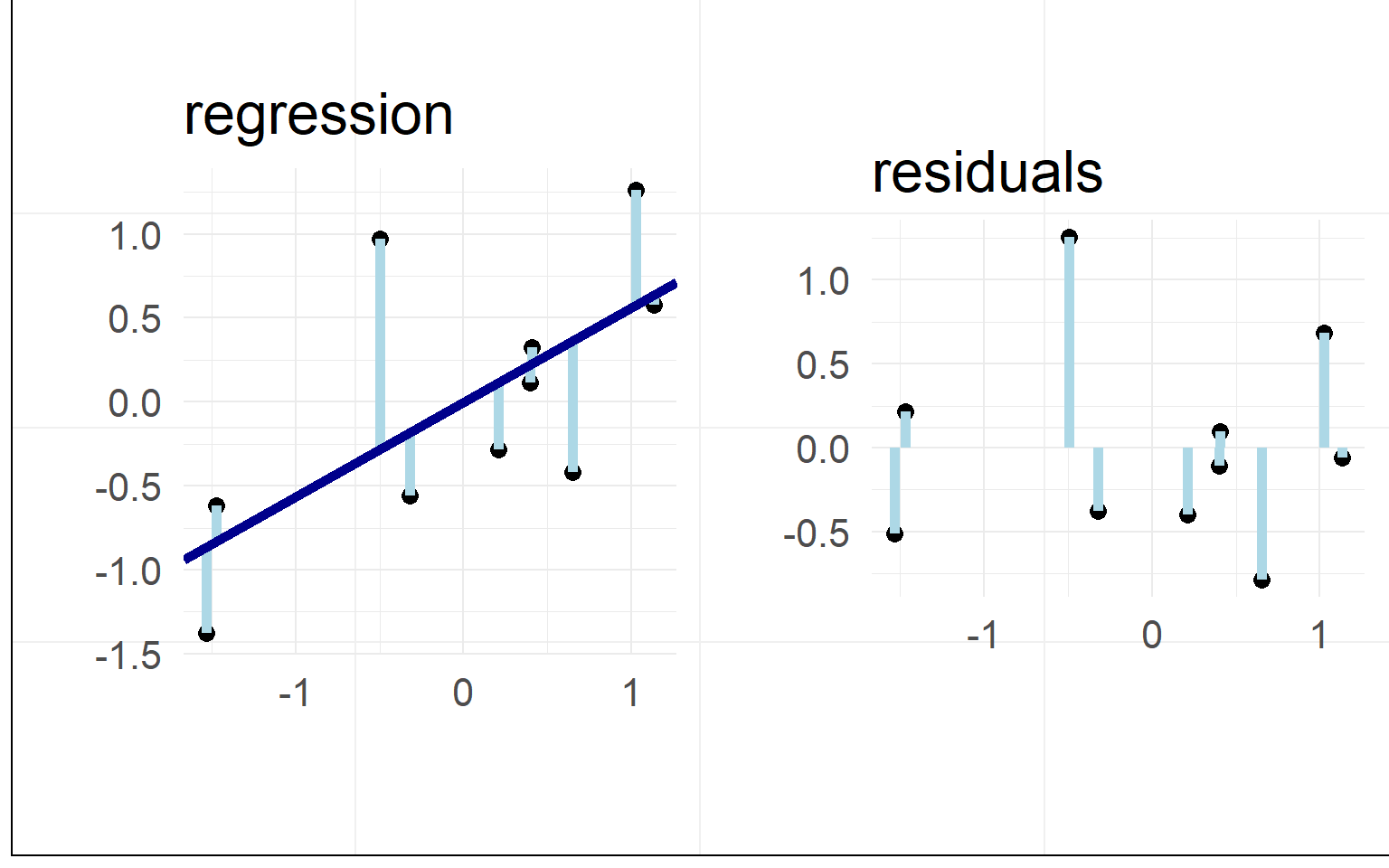
Minimizing the residuals maximizes the fit
L2-Norm (Least Squares): \(min(|residual_i|_2)\)
In our example
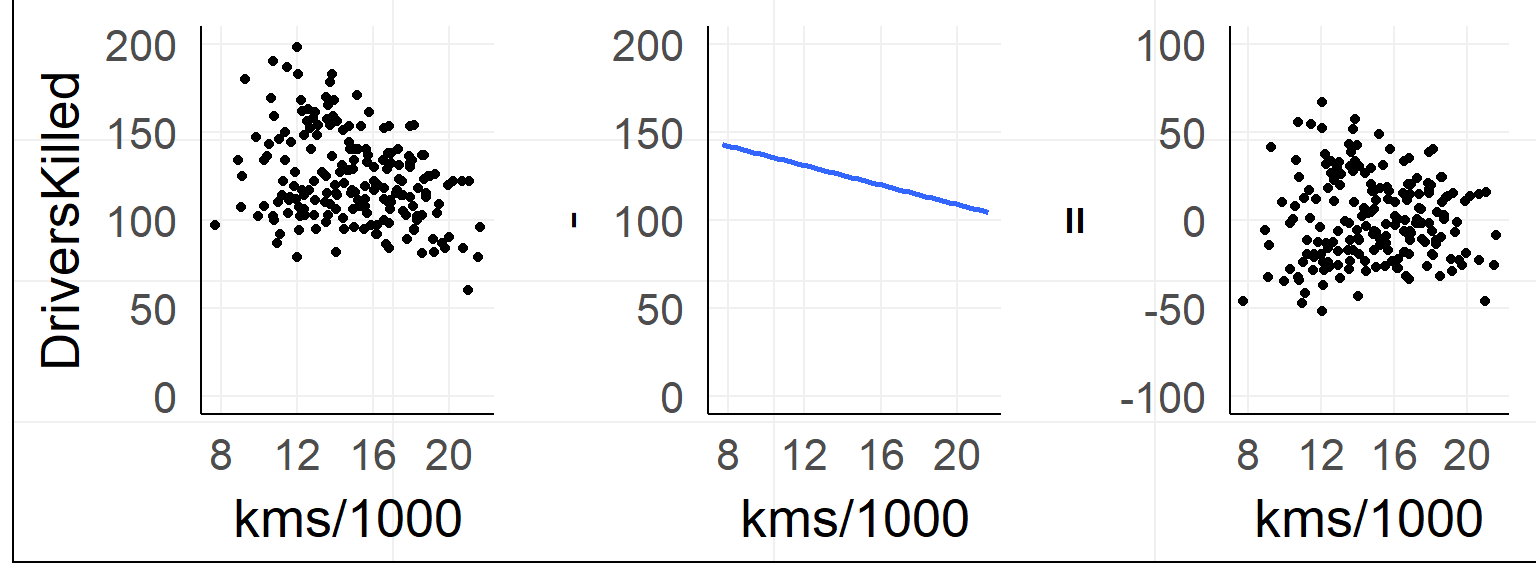
Data: \(y = \beta_0 + x_1 \beta_1 + e_i\)
Prediction: \(\hat{y} = \beta_0 + x_1 \beta_1\)
Residuals: \(e_i = y - \hat{y}\)
in R
summary(lm(formula = DriversKilled ~ 1 + kms,data=data))##
## Call:
## lm(formula = DriversKilled ~ 1 + kms, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -52.028 -19.021 -1.974 16.719 66.964
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.644e+02 9.067e+00 18.130 < 2e-16 ***
## kms -2.774e-03 5.935e-04 -4.674 5.6e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24.1 on 190 degrees of freedom
## Multiple R-squared: 0.1031, Adjusted R-squared: 0.09839
## F-statistic: 21.84 on 1 and 190 DF, p-value: 5.596e-06Explained Variance
(I modified the example data for clarity)
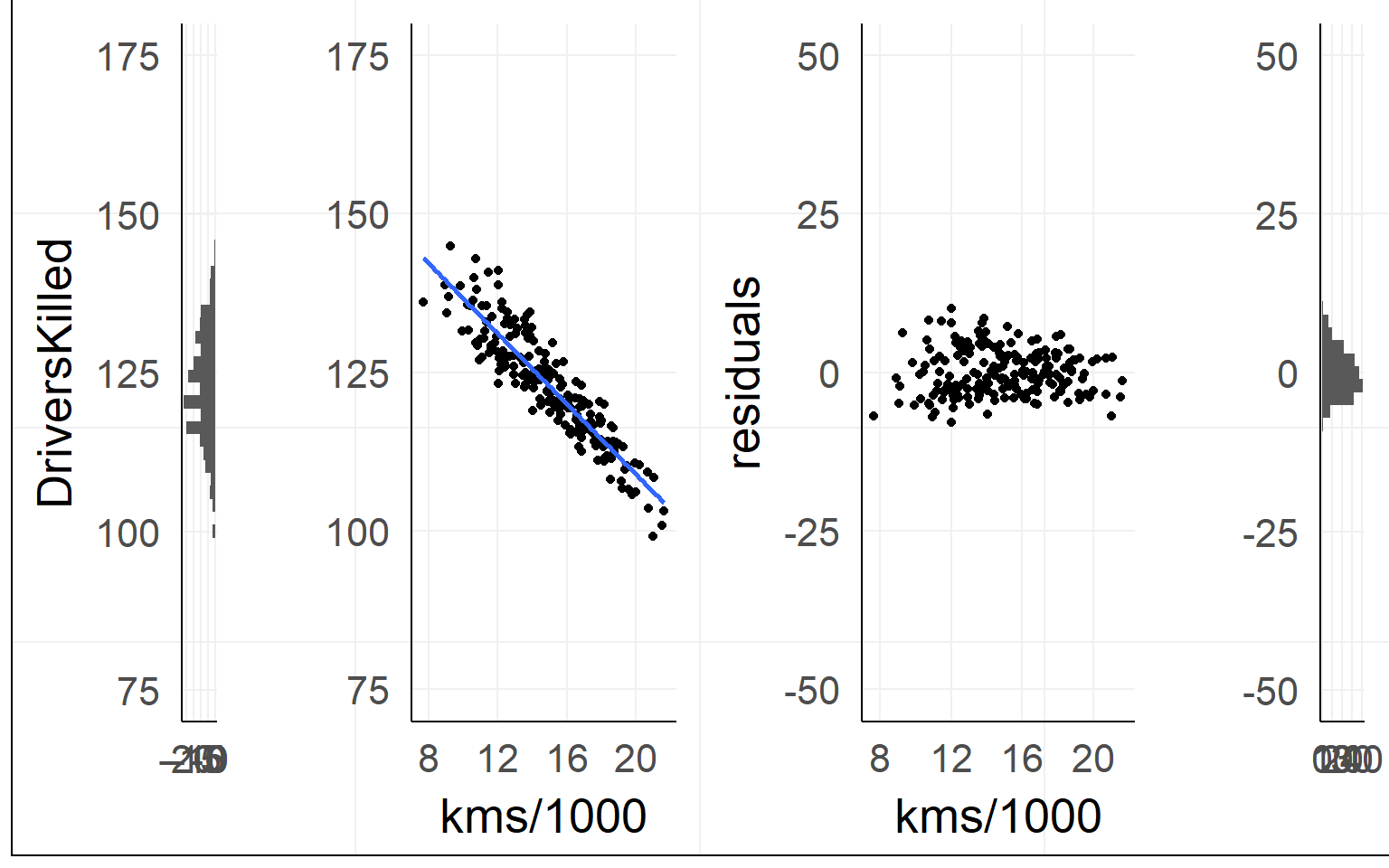
Single outlier
 Especially true for small sample sizes
Especially true for small sample sizes
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
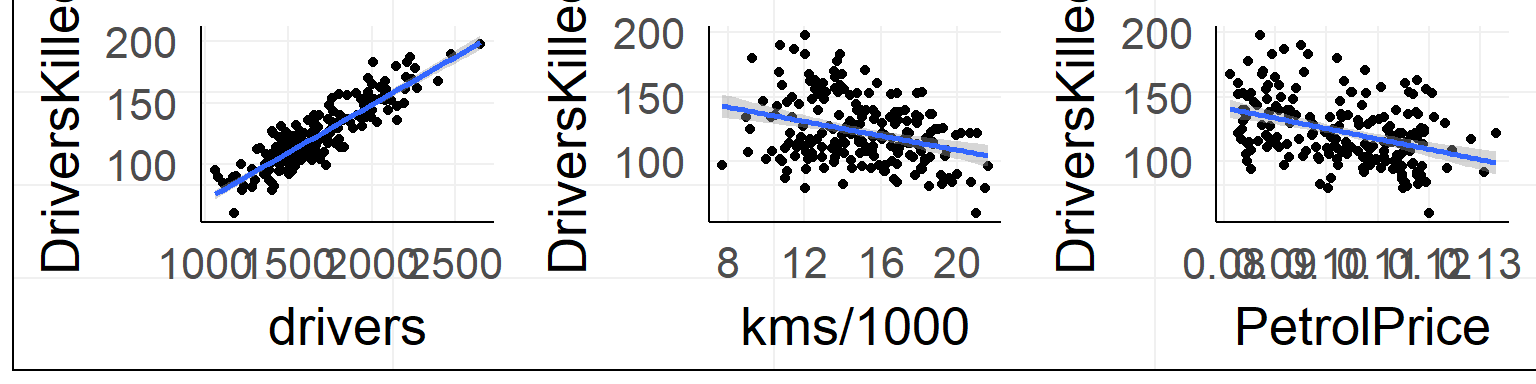
summary(lm(DriversKilled ~ kms + drivers + PetrolPrice,data = data))##
## Call:
## lm(formula = DriversKilled ~ kms + drivers + PetrolPrice, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -27.333 -7.848 -0.532 7.544 35.036
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.642e+01 1.254e+01 -2.107 0.0365 *
## kms 7.901e-04 3.255e-04 2.428 0.0161 *
## drivers 8.164e-02 3.429e-03 23.810 <2e-16 ***
## PetrolPrice 9.716e+00 7.911e+01 0.123 0.9024
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.53 on 188 degrees of freedom
## Multiple R-squared: 0.7969, Adjusted R-squared: 0.7937
## F-statistic: 245.9 on 3 and 188 DF, p-value: < 2.2e-16With two predictors you span a plane
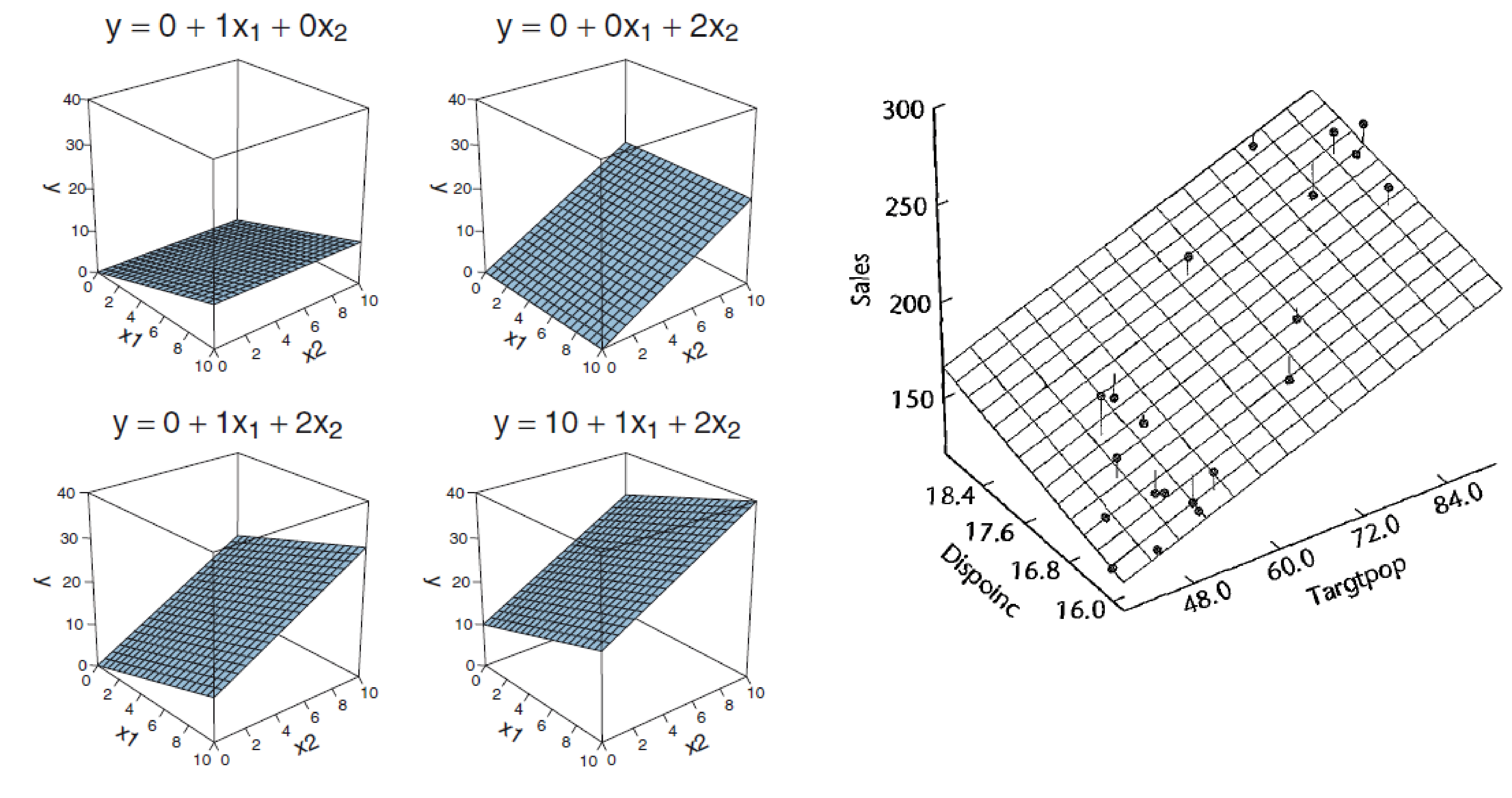
Overlapping variance
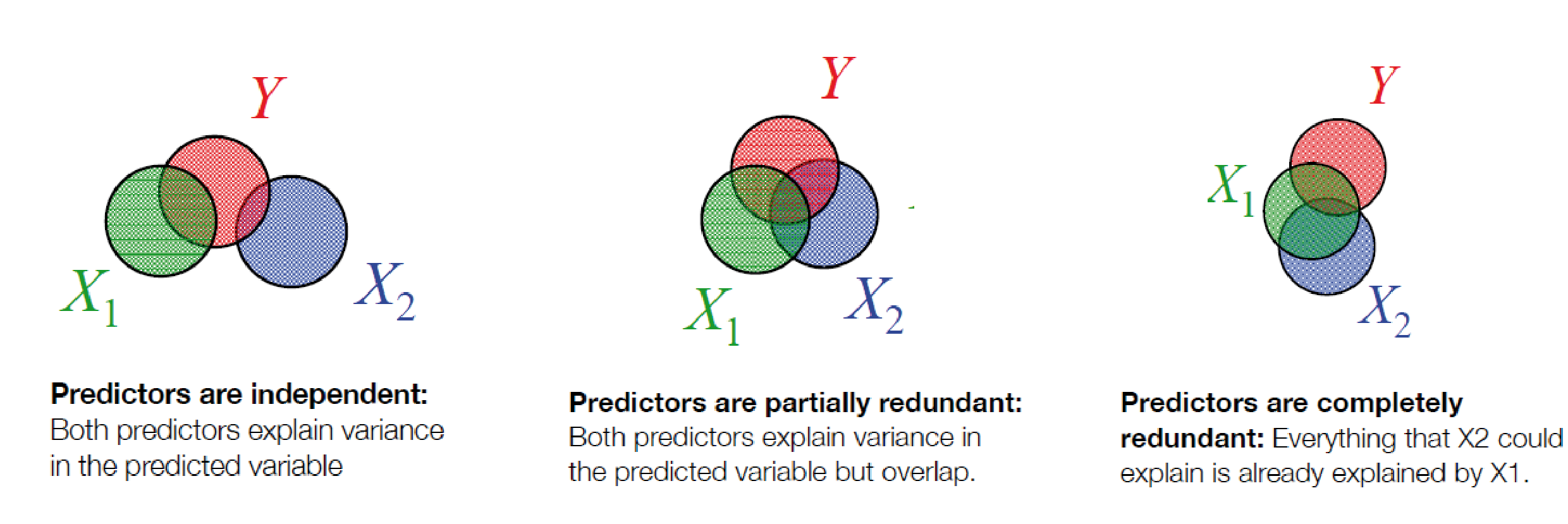
Perfect redundant
data_redundant = data
data_redundant$meters = data_redundant$kms*1000
summary(lm(DriversKilled ~ meters + kms,data = data_redundant))##
## Call:
## lm(formula = DriversKilled ~ meters + kms, data = data_redundant)
##
## Residuals:
## Min 1Q Median 3Q Max
## -52.028 -19.021 -1.974 16.719 66.964
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.644e+02 9.067e+00 18.130 < 2e-16 ***
## meters -2.774e-06 5.935e-07 -4.674 5.6e-06 ***
## kms NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24.1 on 190 degrees of freedom
## Multiple R-squared: 0.1031, Adjusted R-squared: 0.09839
## F-statistic: 21.84 on 1 and 190 DF, p-value: 5.596e-06Partially redundant
data_redundant = data
data_redundant$driversnoise = data_redundant$drivers+rnorm(nrow(data_redundant),sd=10)
coef(summary(lm(DriversKilled ~ drivers,data = data_redundant)))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.30112028 4.938443950 -1.478425 1.409499e-01
## drivers 0.07789178 0.002913364 26.736024 2.636268e-66coef(summary(lm(DriversKilled ~ drivers+driversnoise,data = data_redundant)))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.31191485 4.95029664 -1.4770660 0.1413223
## drivers 0.04903418 0.09120555 0.5376228 0.5914700
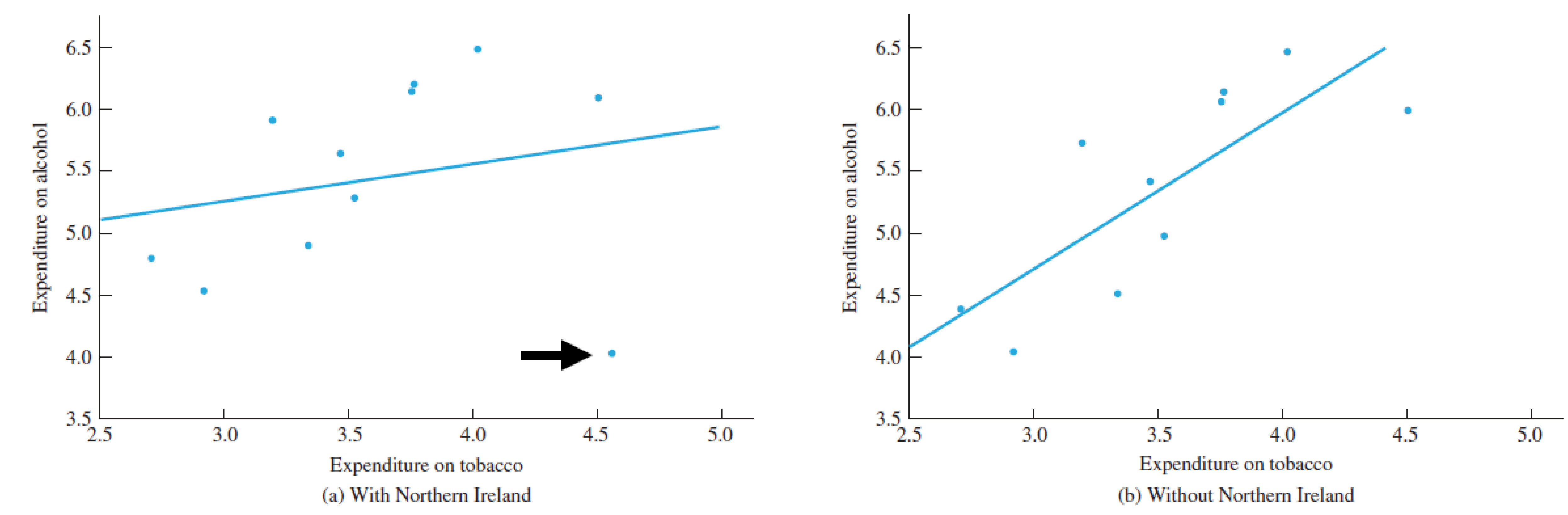
## driversnoise 0.02885613 0.09115416 0.3165641 0.7519237Multicollinearity is usually not so obvious
Surpressors: Including unrelated variables can improve modelfit
##
## Call: lm(formula = Y ~ OV + S)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.01890 0.01838 -1.028 0.308
## OV 0.99939 0.01798 55.574 <1e-04 ***
## S 0.99859 0.01807 55.252 <1e-04 ***
##
## Residual standard error: 0.1411 on 57 degrees of freedom
## Multiple R-squared: 0.9819, Adjusted R-squared: 0.9812
## F-statistic: 1544 on 2 and 57 DF, p-value: < 1e-04##
## Call: lm(formula = Y ~ OV)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.04080 0.13452 -0.303 0.763
## OV 0.01284 0.01565 0.820 0.415
##
## Residual standard error: 1.033 on 58 degrees of freedom
## Multiple R-squared: 0.01147, Adjusted R-squared: -0.005571
## F-statistic: 0.6731 on 1 and 58 DF, p-value: 0.4153a graphical intuition
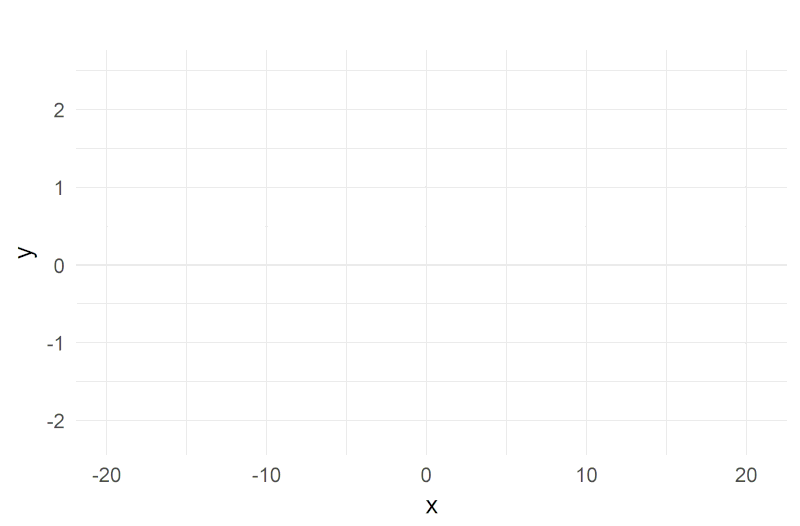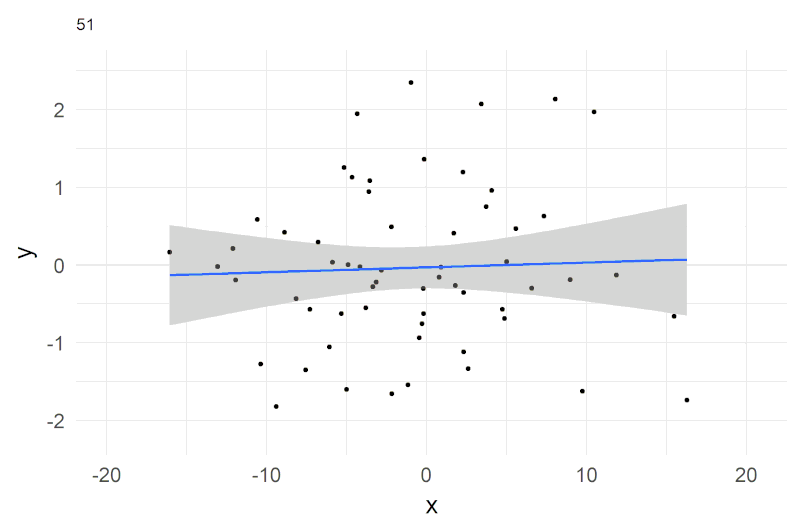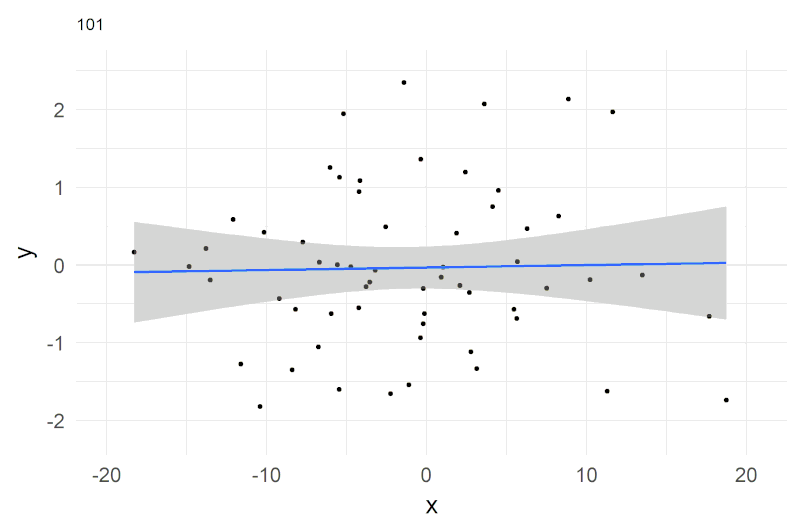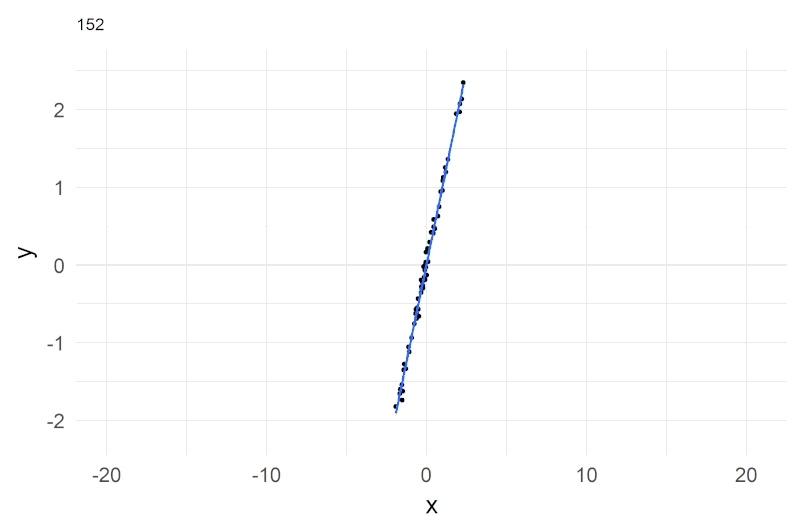
A shorthand notation
\(y_i = 1*\beta_0 + x_{i,1}*\beta_1 + x_{i,2}*\beta_2 + ... + x_{i,n}*\beta_n + e_i\)
is nothing else than matrix multiplication
\(y = X\beta+e\)
\(X = designmatrix\) with size \([n_{datapoints},n_{predictors}]\)
\(e = residuals\)with size \([n_{datapoints}]\)Designmatrix & algebra
## (Intercept) kms drivers PetrolPrice
## 1 1 9059 1687 0.10297181
## 2 1 7685 1508 0.10236300
## 3 1 9963 1507 0.10206249
## 4 1 10955 1385 0.10087330
## 5 1 11823 1632 0.10101967
## 6 1 12391 1511 0.10058119
## 7 1 13460 1559 0.10377398
## 8 1 14055 1630 0.10407640
## 9 1 12106 1579 0.10377398
## 10 1 11372 1653 0.10302640
## 11 1 9834 2152 0.10273011
## 12 1 9267 2148 0.10199719
## 13 1 9130 1752 0.10127456
## 14 1 8933 1765 0.10070398
## 15 1 11000 1717 0.10013961
## 16 1 10733 1558 0.09862110
## 17 1 12912 1575 0.09834929
## 18 1 12926 1520 0.09808018
## 19 1 13990 1805 0.09727921
## 20 1 14926 1800 0.09741062
## 21 1 12900 1719 0.09742524
## 22 1 12034 2008 0.09638063
## 23 1 10643 2242 0.09573896
## 24 1 10742 2478 0.09510631
## 25 1 10266 2030 0.09673597
## 26 1 10281 1655 0.09610922
## 27 1 11527 1693 0.09536725
## 28 1 12281 1623 0.09470959
## 29 1 13587 1805 0.09411762
## 30 1 13049 1746 0.09353215
## 31 1 16055 1795 0.09295405
## 32 1 15220 1926 0.09283979
## 33 1 13824 1619 0.09272474
## 34 1 12729 1992 0.09226965
## 35 1 11467 2233 0.09170669
## 36 1 11351 2192 0.09126207
## 37 1 10803 2080 0.09071160
## 38 1 10548 1768 0.09027633
## 39 1 12368 1835 0.08995192
## 40 1 13311 1569 0.08909964
## 41 1 13885 1976 0.08867919
## 42 1 14088 1853 0.08815929
## 43 1 16932 1965 0.08890206
## 44 1 16164 1689 0.08818133
## 45 1 14883 1778 0.08894029
## 46 1 13532 1976 0.08772661
## 47 1 12220 2397 0.08742885
## 48 1 12025 2654 0.08703543
## 49 1 11692 2097 0.08644992
## 50 1 11081 1963 0.08587264
## 51 1 13745 1677 0.08539822
## 52 1 14382 1941 0.08382198
## 53 1 14391 2003 0.08459078
## 54 1 15597 1813 0.08413690
## 55 1 16834 2012 0.08377841
## 56 1 17282 1912 0.08351074
## 57 1 15779 2084 0.08280639
## 58 1 13946 2080 0.08117889
## 59 1 12701 2118 0.08285361
## 60 1 10431 2150 0.09419012
## 61 1 11616 1608 0.09239984
## 62 1 10808 1503 0.10816148
## 63 1 12421 1548 0.10721169
## 64 1 13605 1382 0.11404297
## 65 1 14455 1731 0.11245412
## 66 1 15019 1798 0.11131625
## 67 1 15662 1779 0.11030125
## 68 1 16745 1887 0.10819718
## 69 1 14717 2004 0.10702744
## 70 1 13756 2077 0.10494698
## 71 1 12531 2092 0.11935775
## 72 1 12568 2051 0.11762190
## 73 1 11249 1577 0.13302742
## 74 1 11096 1356 0.13084524
## 75 1 12637 1652 0.12831848
## 76 1 13018 1382 0.12354745
## 77 1 15005 1519 0.11858681
## 78 1 15235 1421 0.11633748
## 79 1 15552 1442 0.11516148
## 80 1 16905 1543 0.11450120
## 81 1 14776 1656 0.11352298
## 82 1 14104 1561 0.11193018
## 83 1 12854 1905 0.11061053
## 84 1 12956 2199 0.11527439
## 85 1 12177 1473 0.11379349
## 86 1 11918 1655 0.11234958
## 87 1 13517 1407 0.11175347
## 88 1 14417 1395 0.10964252
## 89 1 15911 1530 0.10844090
## 90 1 15589 1309 0.10788494
## 91 1 16543 1526 0.10908477
## 92 1 17925 1327 0.10757145
## 93 1 15406 1627 0.10616402
## 94 1 14601 1748 0.10630000
## 95 1 13107 1958 0.10482531
## 96 1 12268 2274 0.10345175
## 97 1 11972 1648 0.10144992
## 98 1 12028 1401 0.10040232
## 99 1 14033 1411 0.09886203
## 100 1 14244 1403 0.10249615
## 101 1 15287 1394 0.10302743
## 102 1 16954 1520 0.10217891
## 103 1 17361 1528 0.09983664
## 104 1 17694 1643 0.09263669
## 105 1 16222 1515 0.09181496
## 106 1 14969 1685 0.09072430
## 107 1 13624 2000 0.09002121
## 108 1 13842 2215 0.08933071
## 109 1 12387 1956 0.08844273
## 110 1 11608 1462 0.08835257
## 111 1 15021 1563 0.08675736
## 112 1 14834 1459 0.08499524
## 113 1 16565 1446 0.08456794
## 114 1 16882 1622 0.08443190
## 115 1 18012 1657 0.08435088
## 116 1 18855 1638 0.08360098
## 117 1 17243 1643 0.08341726
## 118 1 16045 1683 0.08274514
## 119 1 14745 2050 0.08523527
## 120 1 13726 2262 0.08477030
## 121 1 11196 1813 0.08445892
## 122 1 12105 1445 0.08535212
## 123 1 14723 1762 0.08755921
## 124 1 15582 1461 0.09038292
## 125 1 16863 1556 0.09078329
## 126 1 16758 1431 0.10874278
## 127 1 17434 1427 0.11414223
## 128 1 18359 1554 0.11299293
## 129 1 17189 1645 0.11132071
## 130 1 16909 1653 0.10912623
## 131 1 15380 2016 0.10769846
## 132 1 15161 2207 0.10760157
## 133 1 14027 1665 0.10377502
## 134 1 14478 1361 0.10711417
## 135 1 16155 1506 0.10737477
## 136 1 16585 1360 0.11169537
## 137 1 18117 1453 0.11063818
## 138 1 17552 1522 0.11185521
## 139 1 18299 1460 0.10974234
## 140 1 19361 1552 0.10819393
## 141 1 17924 1548 0.10625536
## 142 1 17872 1827 0.10419303
## 143 1 16058 1737 0.10193397
## 144 1 15746 1941 0.10279382
## 145 1 15226 1474 0.10476034
## 146 1 14932 1458 0.10400254
## 147 1 16846 1542 0.11665552
## 148 1 16854 1404 0.11516148
## 149 1 18146 1522 0.11298954
## 150 1 17559 1385 0.11386064
## 151 1 18655 1641 0.11911808
## 152 1 19453 1510 0.12448999
## 153 1 17923 1681 0.12322295
## 154 1 17915 1938 0.12067793
## 155 1 16496 1868 0.12104898
## 156 1 13544 1726 0.11696857
## 157 1 13601 1456 0.11275026
## 158 1 15667 1445 0.10807931
## 159 1 17358 1456 0.10883852
## 160 1 18112 1365 0.11129177
## 161 1 18581 1487 0.11130401
## 162 1 18759 1558 0.11545436
## 163 1 20668 1488 0.11476830
## 164 1 21040 1684 0.11720743
## 165 1 18993 1594 0.11907640
## 166 1 18668 1850 0.11796586
## 167 1 16768 1998 0.11744913
## 168 1 16551 2079 0.11698846
## 169 1 16231 1494 0.11261054
## 170 1 15511 1057 0.11365702
## 171 1 18308 1218 0.11314445
## 172 1 17793 1168 0.11849553
## 173 1 19205 1236 0.11796940
## 174 1 19162 1076 0.11768661
## 175 1 20997 1174 0.12005924
## 176 1 20705 1139 0.11943775
## 177 1 18759 1427 0.11888127
## 178 1 19240 1487 0.11846236
## 179 1 17504 1483 0.11801660
## 180 1 16591 1513 0.11770662
## 181 1 16224 1357 0.11777609
## 182 1 16670 1165 0.11479699
## 183 1 18539 1282 0.11573525
## 184 1 19759 1110 0.11535626
## 185 1 19584 1297 0.11481536
## 186 1 19976 1185 0.11477748
## 187 1 21486 1222 0.11493598
## 188 1 21626 1284 0.11479699
## 189 1 20195 1444 0.11409316
## 190 1 19928 1575 0.11646552
## 191 1 18564 1737 0.11602611
## 192 1 18149 1763 0.11606673\[ y = X\beta\] Can be solved by: \[ \beta = (X^TX)^{-1}X^Ty\] (don’t memorize this)
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
Dummy Coding
Dummy Coding
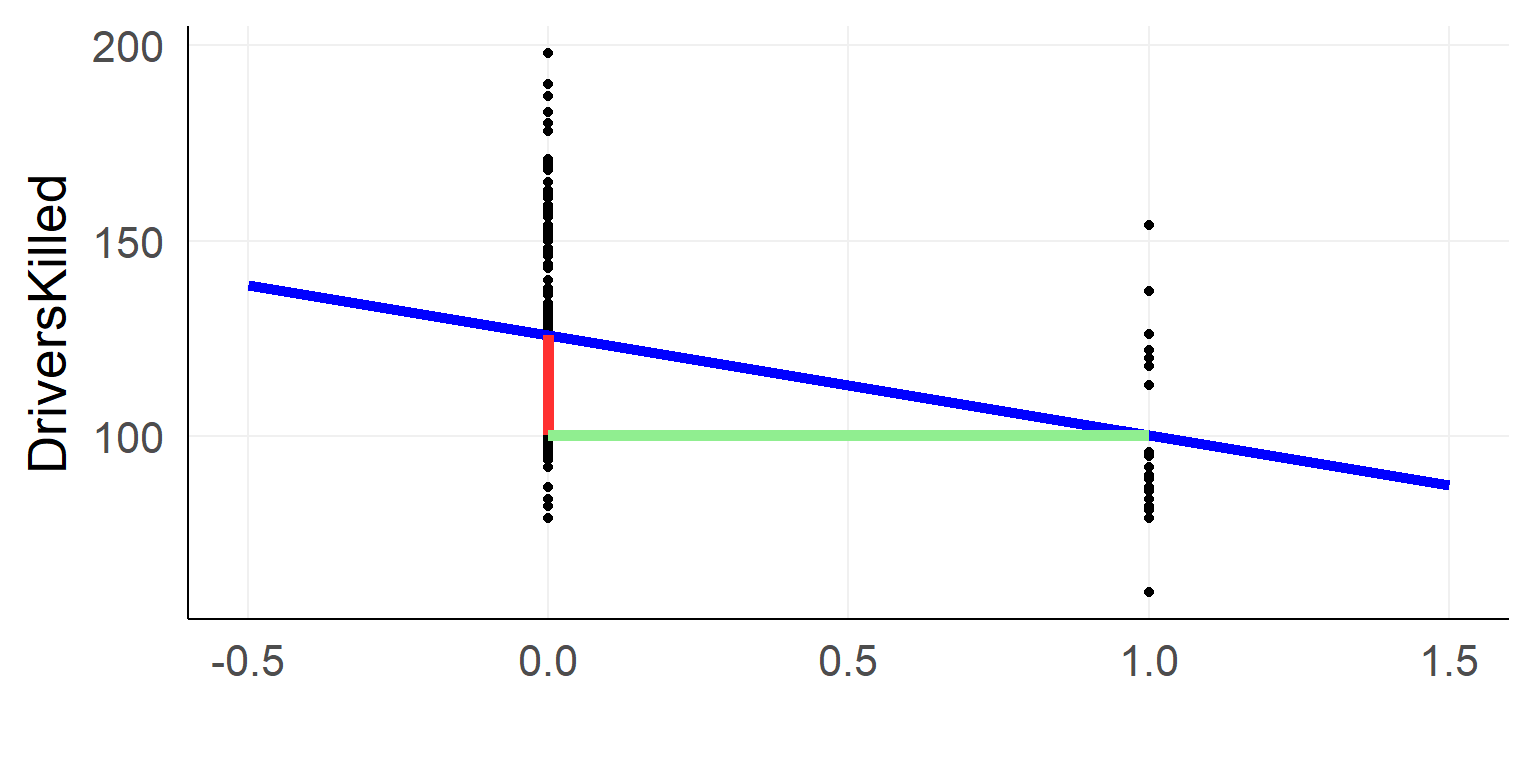
We code the categorical variable with 0 / 1
\(y_i = \beta_0 + is\_law *\beta_1 + e_i\)
Interpretation
\(y_i = \beta_0 + is\_law *\beta_1 + e_i\)
- \(\beta_0\) / Intercept: Driverskilled when \(is\_law\) equals 0
- \(\beta_1\) / Slope: Additional drivers killed when \(is\_law\) was changed to 1
summary(lm(data=data_factor,DriversKilled~1+law))##
## Call:
## lm(formula = DriversKilled ~ 1 + law, data = data_factor)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46.870 -17.870 -5.565 14.130 72.130
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 125.870 1.849 68.082 < 2e-16 ***
## lawwith seatbelt law -25.609 5.342 -4.794 3.29e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24.03 on 190 degrees of freedom
## Multiple R-squared: 0.1079, Adjusted R-squared: 0.1032
## F-statistic: 22.98 on 1 and 190 DF, p-value: 3.288e-06Effect Coding aka sum coding aka deviation coding
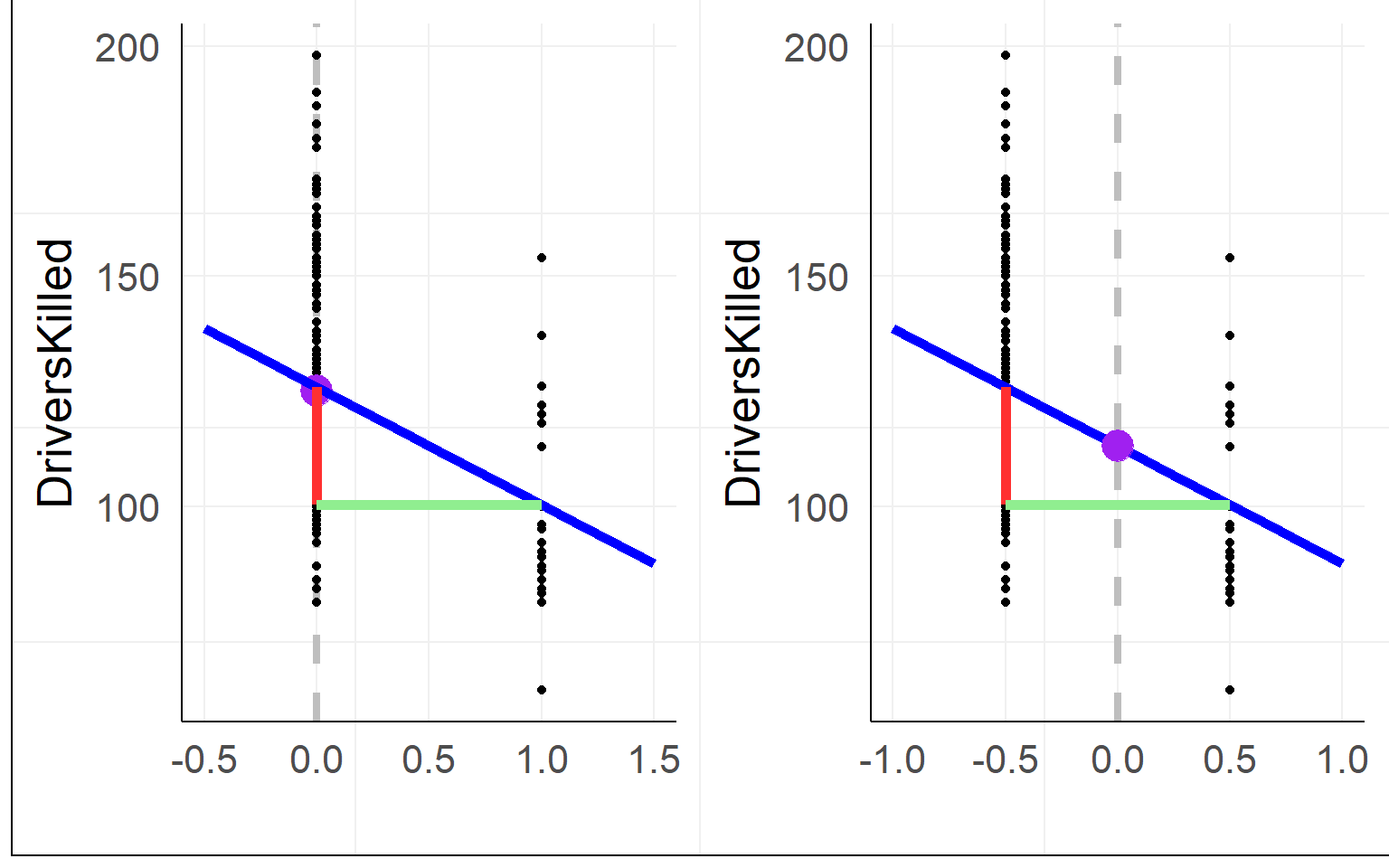
Using effect coding, the interpretation of the intercept changes to the mean between groups
warning: often effect coding is made using -1 and 1, then the \(\beta_1\) is halve the size! using 0.5 is much more practicalMultiple levels
| (Intercept) | factormiddle | factorhigh |
|---|---|---|
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
Treatment / Dummy Coding
| (Intercept) | factor1 | factor2 |
|---|---|---|
| 1 | 0.5 | 0.0 |
| 1 | 0.5 | 0.0 |
| 1 | 0.5 | 0.0 |
| 1 | 0.0 | 0.5 |
| 1 | 0.0 | 0.5 |
| 1 | 0.0 | 0.5 |
| 1 | -0.5 | -0.5 |
| 1 | -0.5 | -0.5 |
| 1 | -0.5 | -0.5 |
Effect Coding
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
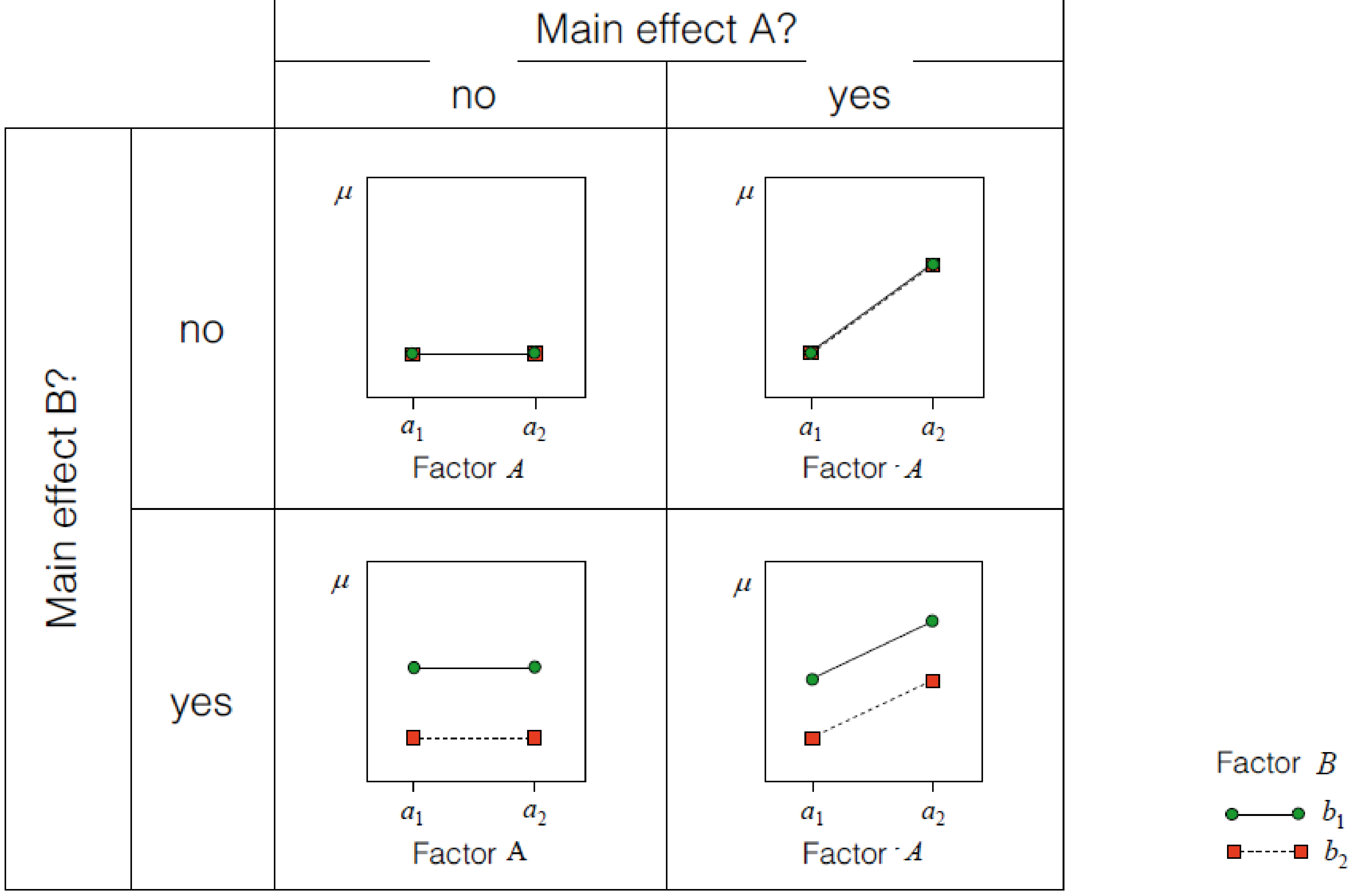 errorbars/data-points ommited for clarity
errorbars/data-points ommited for clarity
Interaction effects
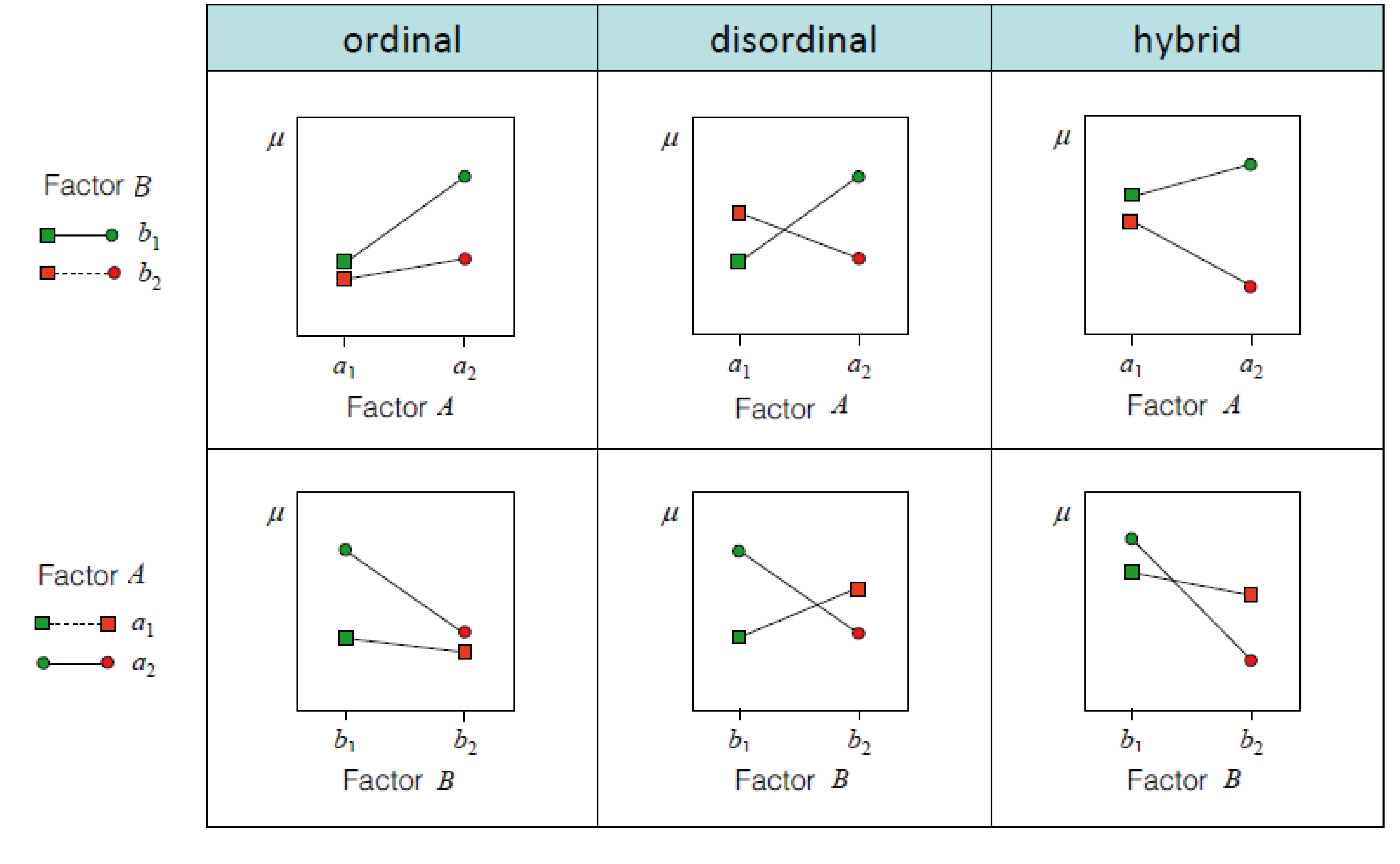
How are interactions coded
\(y = \beta_0 + factorA * \beta_1 + factorB * \beta_2 + factorA * factorB * \beta_3\)
Different words for the same thing:
- The interaction shows how much the prediction needs to be changed, when both factors coocur
- The interaction is the multiplication of the columns in X of factorA and factorB
- The interaction represents the difference of differences
Interactions of continuous/categorical predicotrs
\(y = \beta_0 + factorA * \beta_1 + contB * \beta_2 + factorA * contB * \beta_3\) 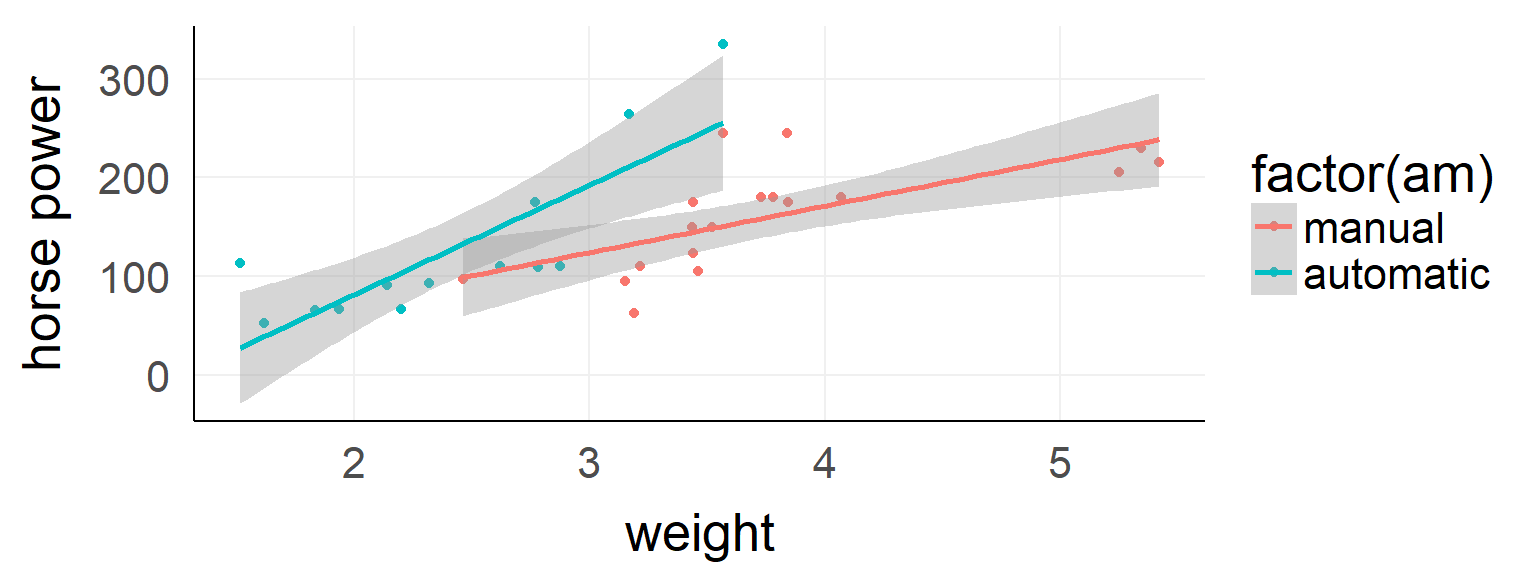
##
## Call: lm(formula = hp ~ wt * am, data = d)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -17.39 52.44 -0.332 0.74260
## wt 47.14 13.64 3.456 0.00177 **
## am -123.33 74.03 -1.666 0.10690
## wt:am 63.84 25.08 2.545 0.01672 *
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: < 1e-04The difference between main and simple effects
Dummy coding tests simple effects
Effect coding main effects
Effect coding to the help!
##
## Call: lm(formula = hp ~ wt * am, data = d)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -17.39 52.44 -0.332 0.74260
## wt 47.14 13.64 3.456 0.00177 **
## am -123.33 74.03 -1.666 0.10690
## wt:am 63.84 25.08 2.545 0.01672 *
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: < 1e-04##
## Call: lm(formula = hp ~ wt * am, data = d)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -79.06 37.02 -2.136 0.0416 *
## wt 79.06 12.54 6.303 <1e-04 ***
## am1 -123.33 74.03 -1.666 0.1069
## wt:am1 63.84 25.08 2.545 0.0167 *
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: < 1e-04Centering continuous predictors
\(weight_{new} = weight - mean(weight)\)
\(y = \beta_0 + weight_{new}*\beta_1 + am*\beta_2 + weight_{new}*am*\beta_3\)
What does \(\beta_1\) and \(\beta_0\) represent now?
##
## Call:
## lm(formula = hp ~ wt_new * am, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -70.976 -24.385 -3.179 14.922 94.112
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 175.29 12.32 14.231 2.42e-14 ***
## wt_new 79.06 12.54 6.303 8.12e-07 ***
## am1 82.06 24.64 3.331 0.00244 **
## wt_new:am1 63.84 25.08 2.545 0.01672 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: 6.266e-06Interaction between two continuous variables
##
## Call:
## lm(formula = read ~ math * socst, data = dSoc)
##
## Residuals:
## Min 1Q Median 3Q Max
## -18.6071 -4.9228 -0.7195 4.5912 21.8592
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.842715 14.545210 2.602 0.00998 **
## math -0.110512 0.291634 -0.379 0.70514
## socst -0.220044 0.271754 -0.810 0.41908
## math:socst 0.011281 0.005229 2.157 0.03221 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.96 on 196 degrees of freedom
## Multiple R-squared: 0.5461, Adjusted R-squared: 0.5392
## F-statistic: 78.61 on 3 and 196 DF, p-value: < 2.2e-16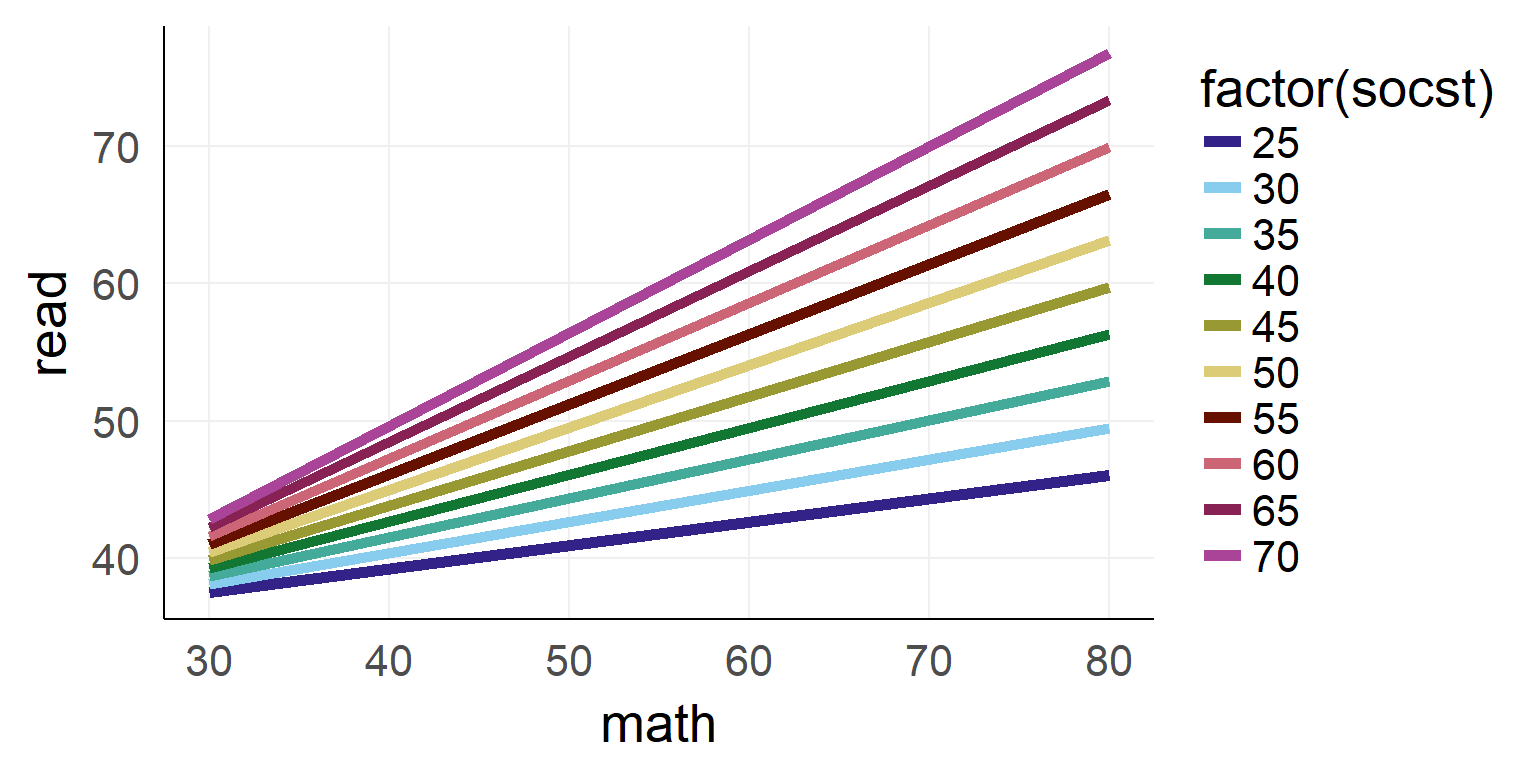
Interaction as a plane
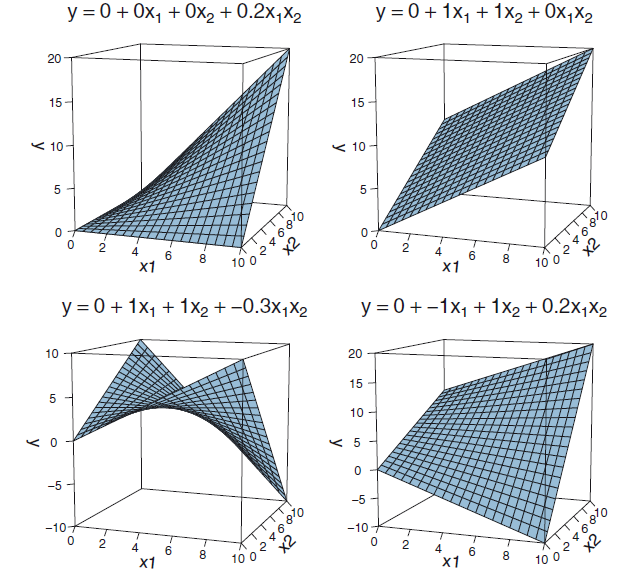
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- single parameter
- model comparison
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
Remember: There is only one statistical test
 We need to specify our H0
We need to specify our H0
General assumption for all of the following inference: Independence of residuals
Two general ways
sampling distribution of predictors (walds t-test)
- walds-t = \(\frac{estimate}{SE}\)
- tests a single predictor
- coding scheme influences what is tested (good and bad)
Model comparison / F-test
- Test how well a model with predictor vs. one without explain the data
- Can test sets of predictors at the same time
Generally the two tests will agree in the case of a single predictor to be tested (\((waldsT)^2 = F\)).
This will be not true when we reach GLMs and in multiple regression only for high \(n\)
What is a standard error?
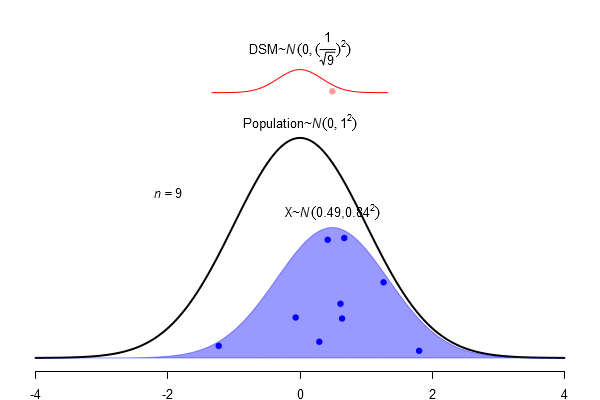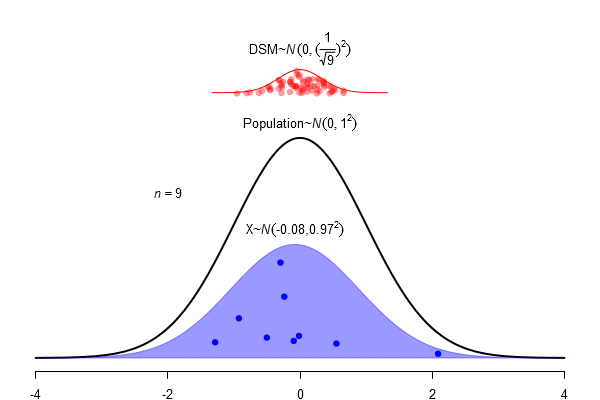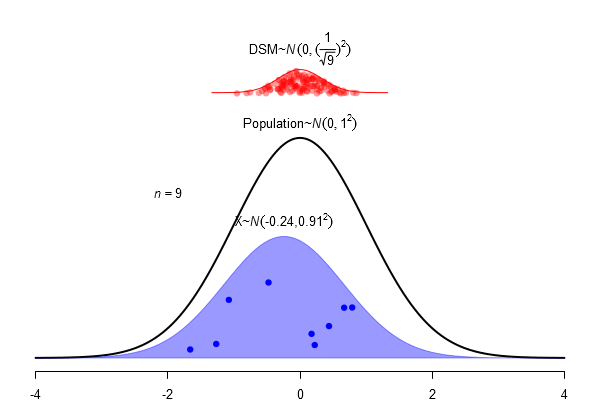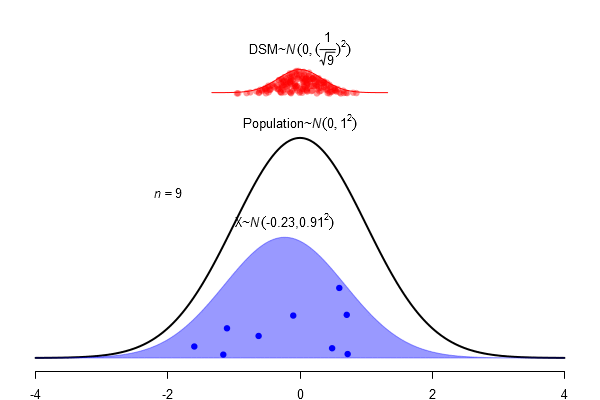
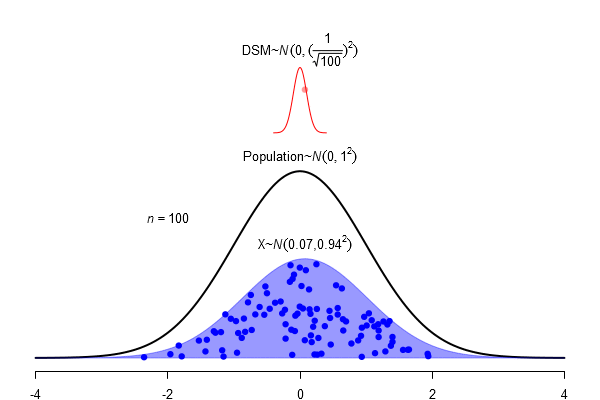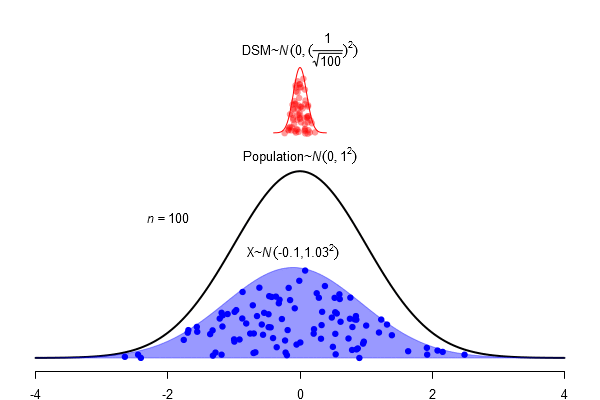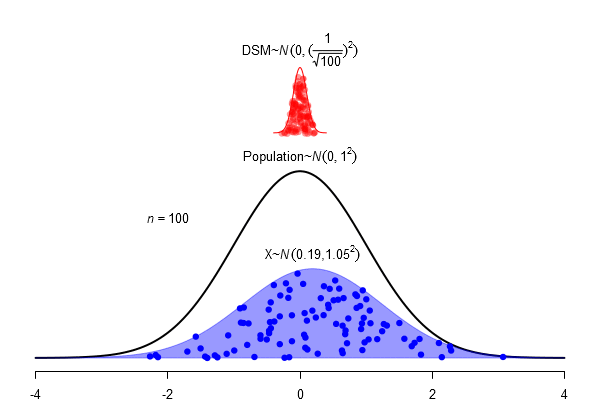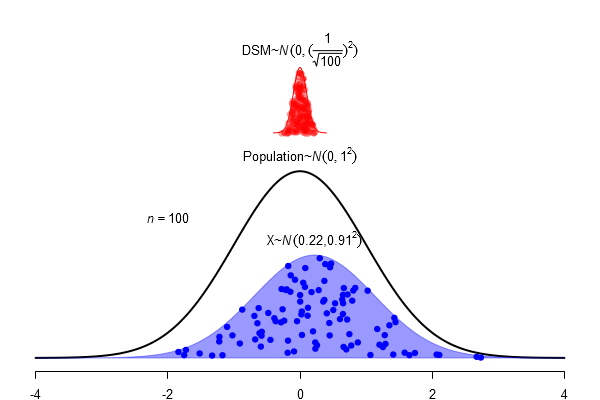
\(SEM = \frac \sigma{\sqrt{N}}\)
Confidence Interval as an area of the sampling distribution
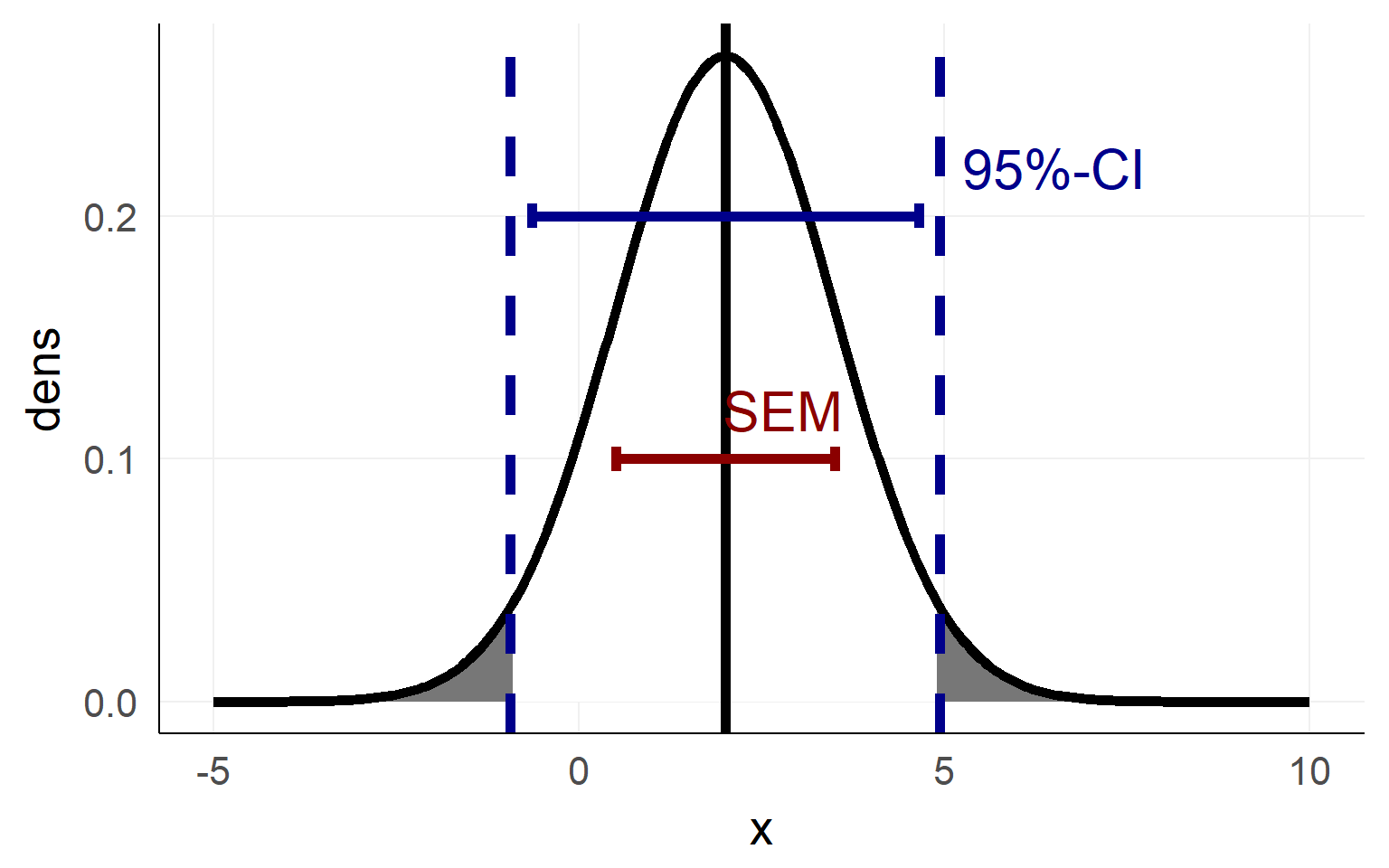
Confidence intervals visualized
Important notes on confidence intervals
An estimated mean \(\hat \mu\) of a population is either in a proposed range (e.g. confidence interval) or its not.
There is not a 95% probability that the population mean \(\mu\) is in a calculated 95%-confidence interval
The 95% are attached to the confidence-interval NOT the mean
=> 95% of confidence-intervals contain the population mean \(\mu\)
- There is no way of knowing whether your confidence interval contains \(\mu\) :(
Just to be sure: Mr. Mean

The \(H_0\) for the simple regression
\(\mu\) - the mean:
- For the intercept (usually): Intercept = 0
- For the slope (usually): slope = 0
But what is the width of the sampling distribution we should use?
In other words: How does the lm function know what the standard errors (\(\frac{\sigma}{sqrt(n)}\)) are?
Expert slide: Estimating standard errors from X
\(\beta = (X^TX)^{-1}X^Ty\)
\(SE = \sqrt{diag(\sigma^2 (X^TX)^{-1})}\)
Quickly summarized: it looks at partial correlations of X (\(X^TX\) => Covariance, inverse => partial correlations) and weights them with the residuals’ variance \(\hat \sigma\)
Walds t-test
summary(fit)##
## Call:
## lm(formula = read ~ math * socst, data = dSoc)
##
## Residuals:
## Min 1Q Median 3Q Max
## -18.6071 -4.9228 -0.7195 4.5912 21.8592
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.842715 14.545210 2.602 0.00998 **
## math -0.110512 0.291634 -0.379 0.70514
## socst -0.220044 0.271754 -0.810 0.41908
## math:socst 0.011281 0.005229 2.157 0.03221 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.96 on 196 degrees of freedom
## Multiple R-squared: 0.5461, Adjusted R-squared: 0.5392
## F-statistic: 78.61 on 3 and 196 DF, p-value: < 2.2e-16\(wald-t = \frac{\beta}{SE}\)
wald-t is not normal distributed but t-distributed
What is a t-distribution?
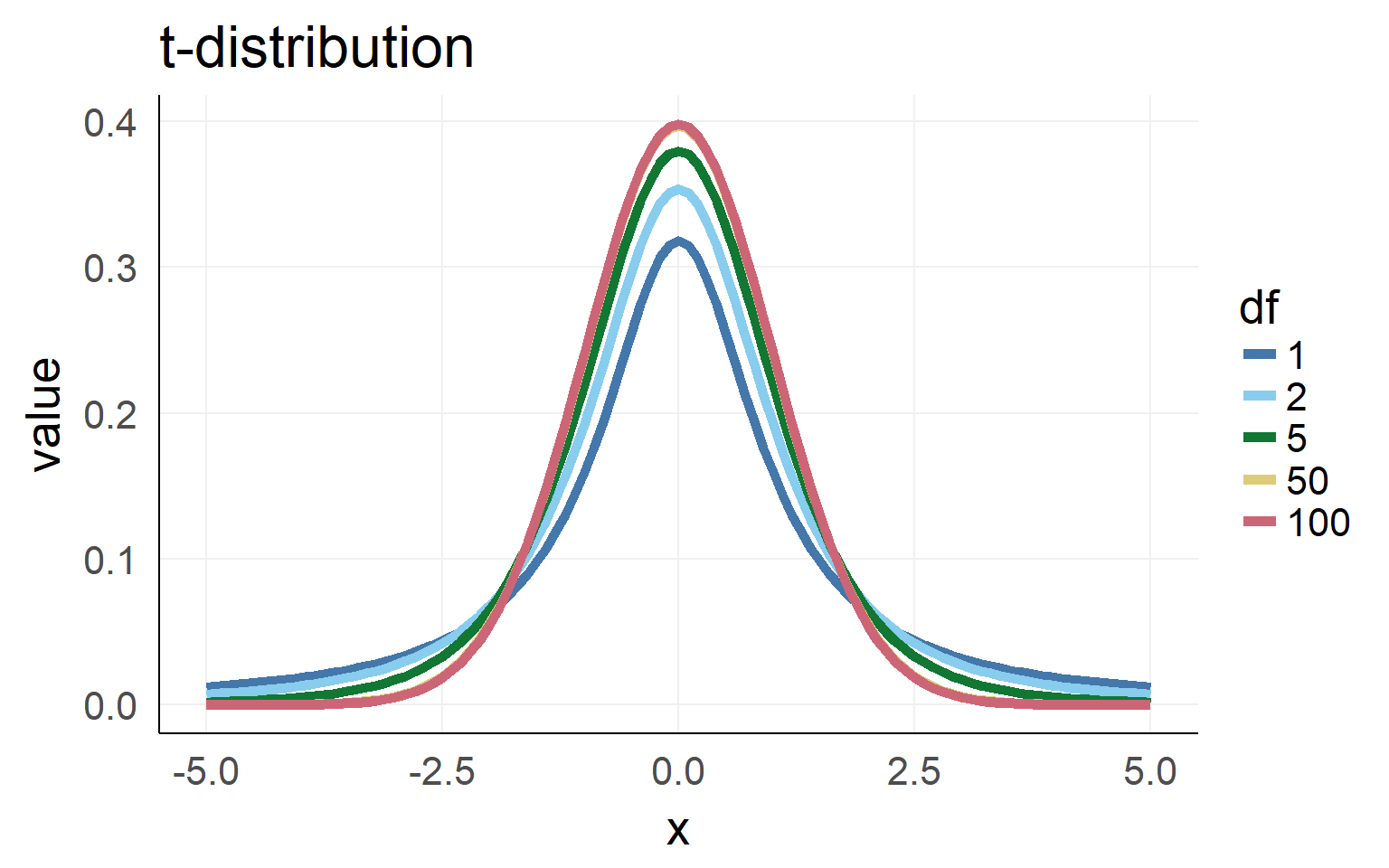
Population \(\sigma\) is unknown. Sampling \(\hat \sigma\) has to be used.
=> Sampling distribution (for small n) is not normal distributed but student t-distributed (with given degrees of freedom)
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- single parameter
- model comparison
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
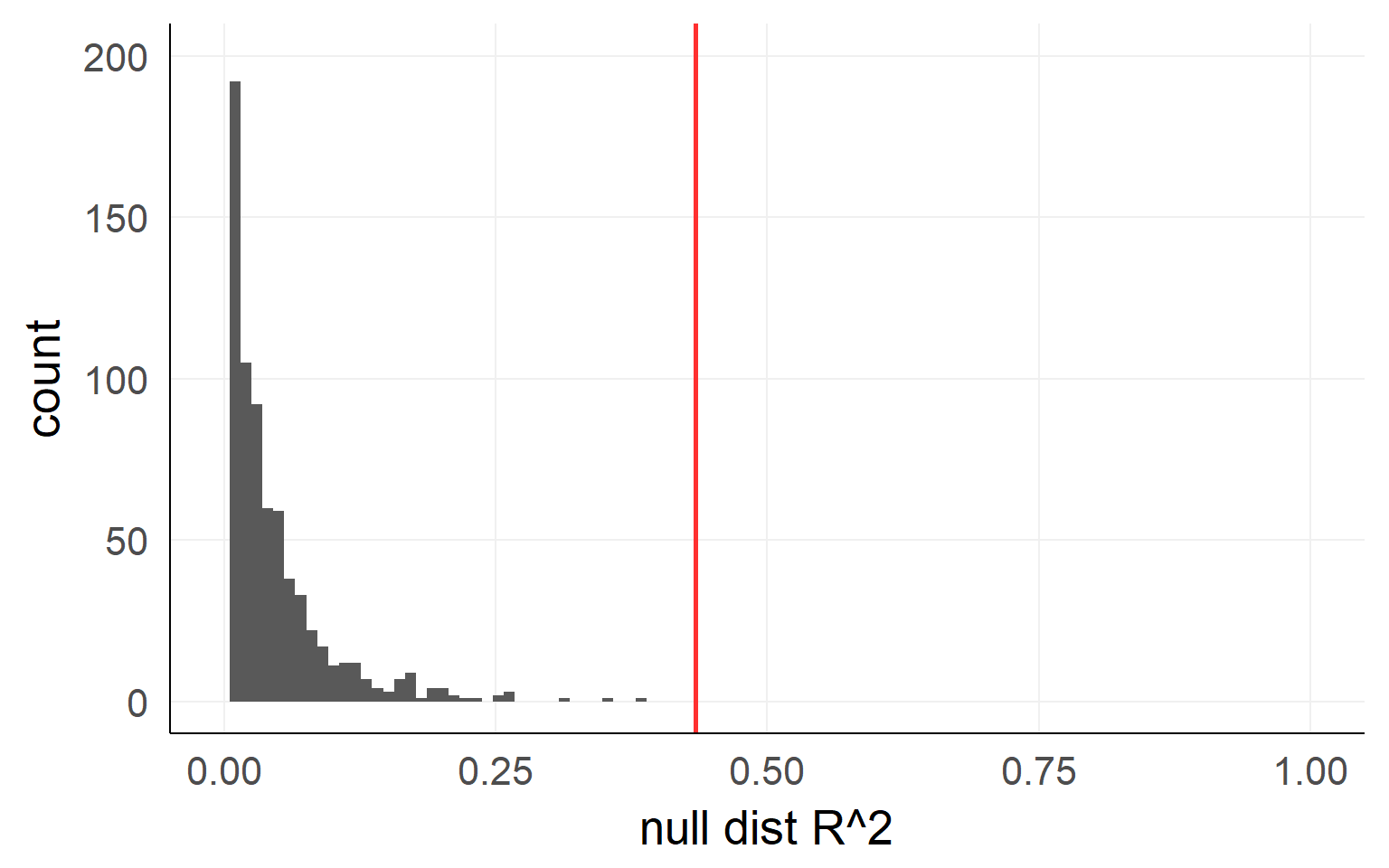
Variance Explained / F-Test
\[R^2 = 1-\frac{var(residual_{full})}{var(residual_{reduced})}\]
In order to get the variance explained of the full/reduced model we need to fit the model twice, once with the effect and once without. Conceptually, the test boils down to:
var1 = var(resid(lm(data=d,hp~1+wt)))
var0 = var(resid(lm(data=d,hp~1)))
r^2 = 1-var1/var0Empirical distribution:
Analytic solution
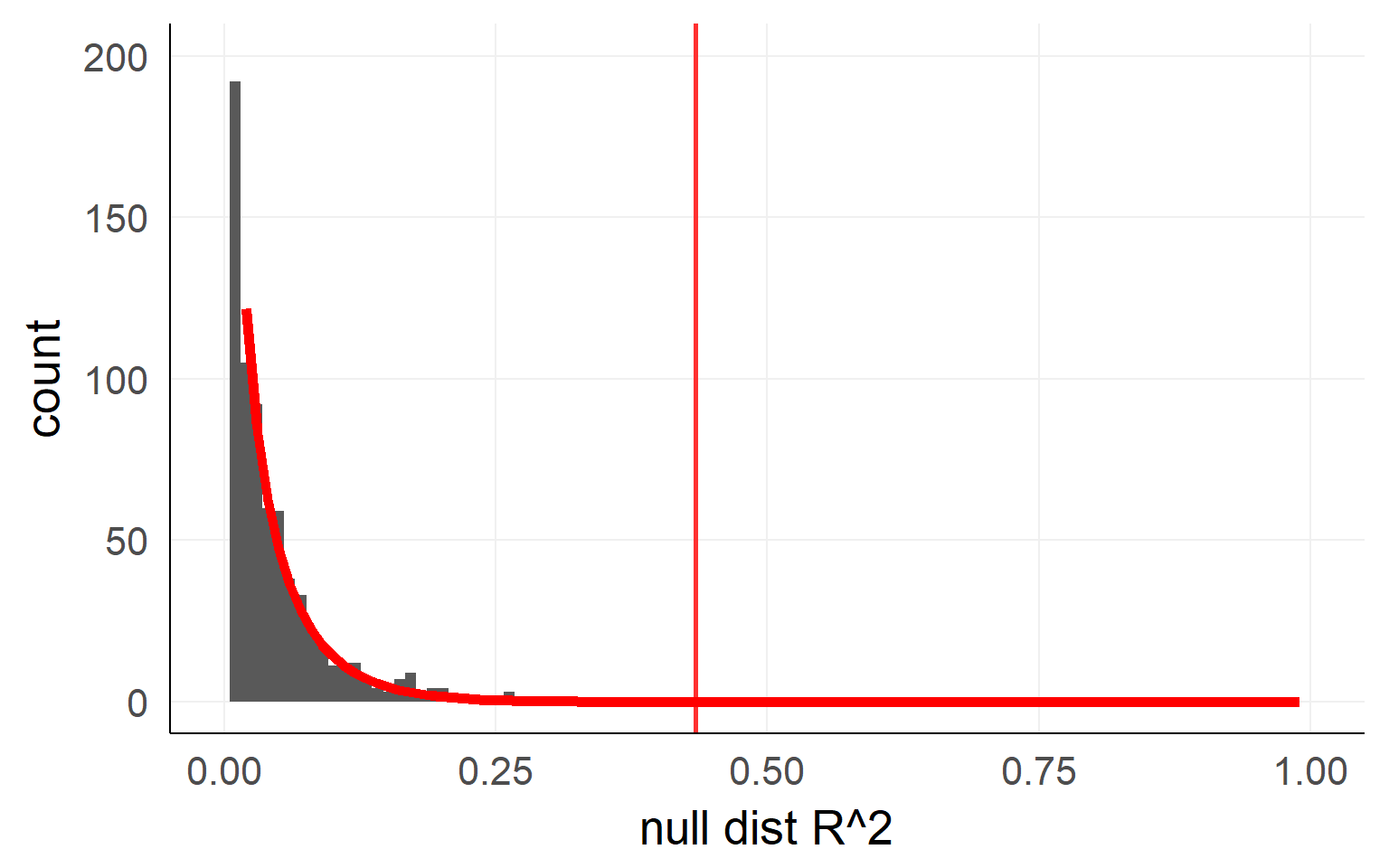
An analytical form is available here as well
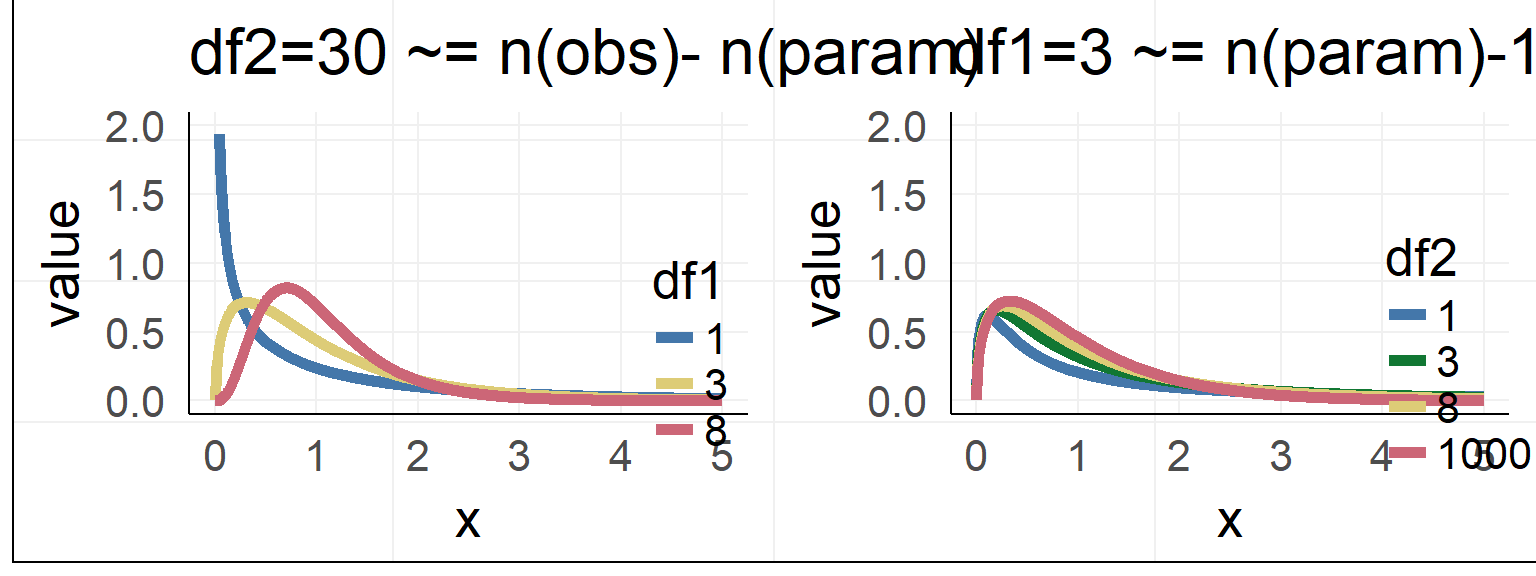
Usually F-distribution is used
\[ F = \frac{\frac{R^2_{m+k}-R^2_{m}}{df_1}}{\frac{1-R^2_{m+k}}{df_2}} = \frac{R^2_{m+k}-R^2_{m}}{1-R^2_{m+k}} * \frac{df_2}{df_1}\] with bookkeeping (for 1xk ANOVA):
\(df_1 = k\), with \(k\) the number of predictors
\(df_2 = n - m - k -1\), with \(n\) the number of observations, \(m\) the number of total predictors
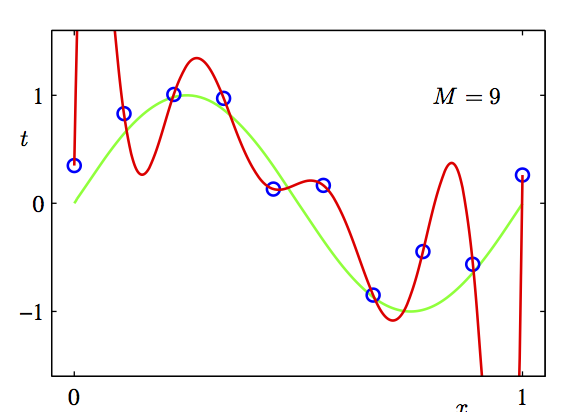
Overfit
var-explained(predictorA) \(<=\) Var-explained(predictorA + predictorB)
Explained-variance is not everything. We also have to take into account the number of predictors we include
Categorical predictor with multiple levels
Airbnb prices against location in Berlin (first 900 entries)
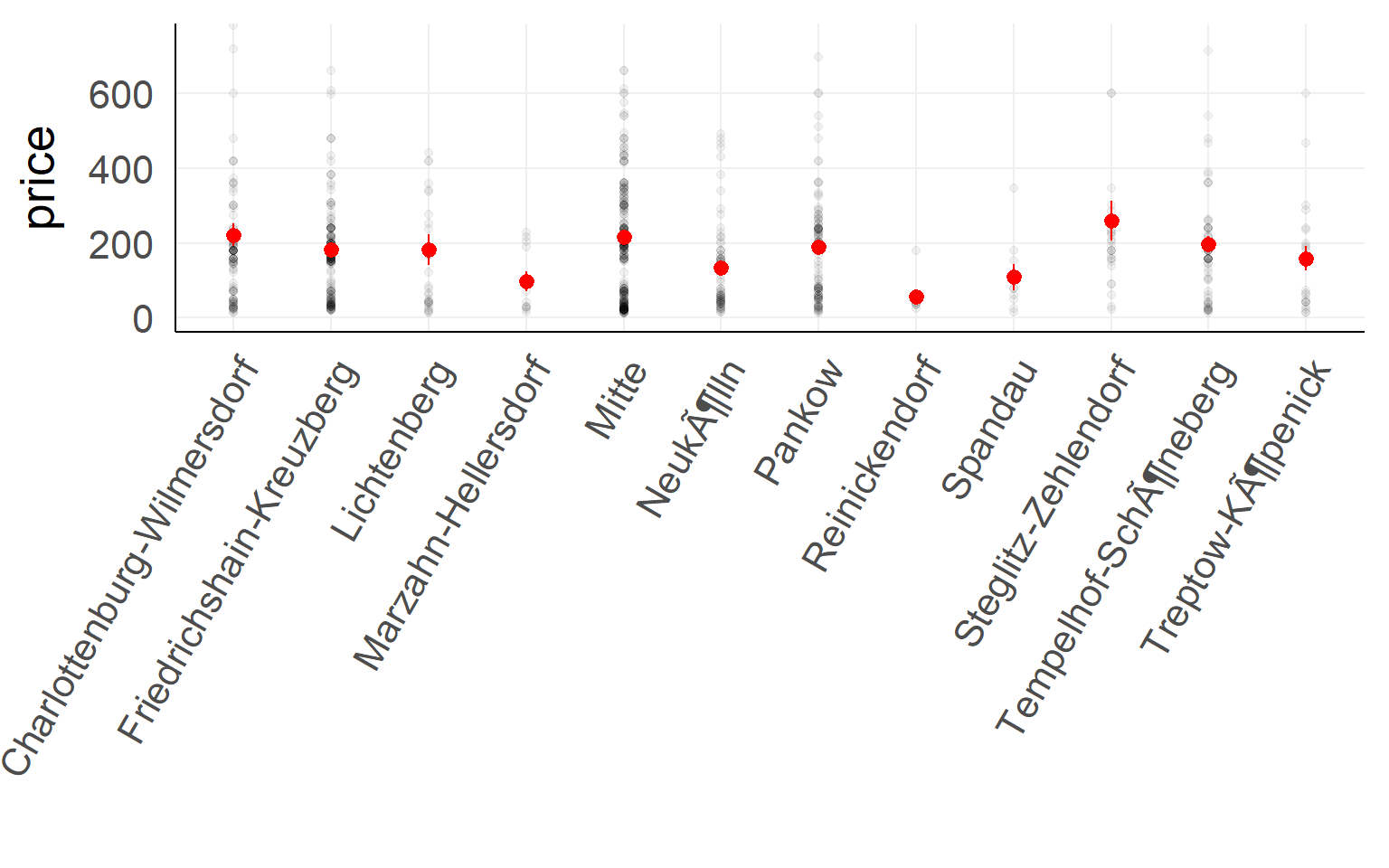
Testing
summary(lm(price~1+ngb,dair[1:900,]))##
## Call:
## lm(formula = price ~ 1 + ngb, data = dair[1:900, ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -237.30 -134.55 -27.47 45.21 2822.60
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 222.113 22.833 9.728 <2e-16 ***
## ngbFriedrichshain-Kreuzberg -38.717 28.353 -1.366 0.1724
## ngbLichtenberg -39.647 46.980 -0.844 0.3989
## ngbMarzahn-Hellersdorf -124.022 71.546 -1.733 0.0834 .
## ngbMitte -6.562 26.621 -0.246 0.8054
## ngbNeukölln -89.534 35.416 -2.528 0.0116 *
## ngbPankow -32.324 31.064 -1.041 0.2984
## ngbReinickendorf -166.256 88.011 -1.889 0.0592 .
## ngbSpandau -112.891 78.361 -1.441 0.1500
## ngbSteglitz-Zehlendorf 37.183 48.933 0.760 0.4475
## ngbTempelhof-Schöneberg -24.770 36.215 -0.684 0.4942
## ngbTreptow-Köpenick -62.896 52.155 -1.206 0.2282
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 224.9 on 888 degrees of freedom
## Multiple R-squared: 0.02032, Adjusted R-squared: 0.008188
## F-statistic: 1.675 on 11 and 888 DF, p-value: 0.07433
Testing
m0 = lm(price~1 ,dair[1:900,])
m1 = lm(price~1+ngb,dair[1:900,])
anova(m0,m1)## Analysis of Variance Table
##
## Model 1: price ~ 1
## Model 2: price ~ 1 + ngb
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 899 45839663
## 2 888 44908040 11 931623 1.6747 0.07433 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1an graphical way to think about it
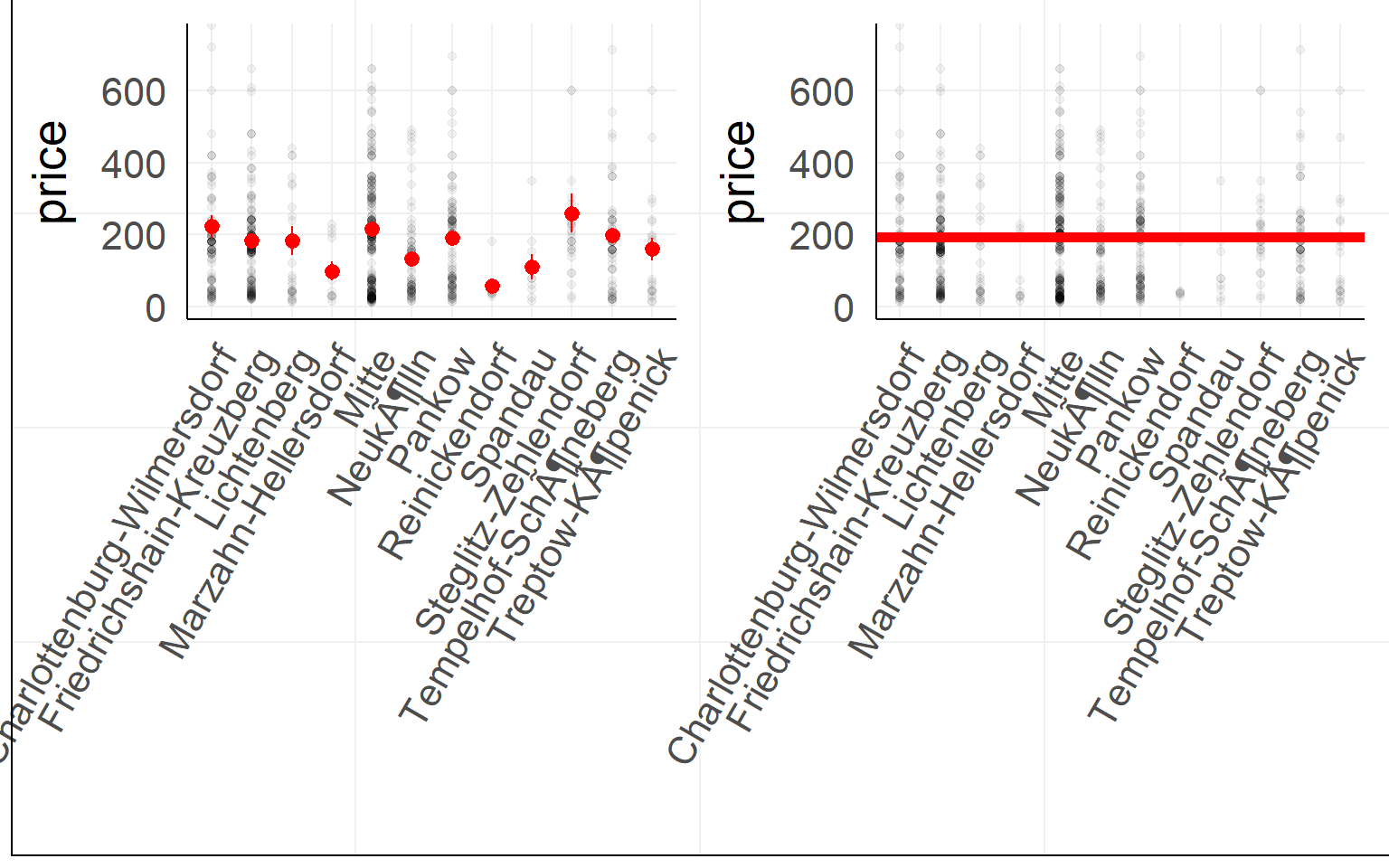
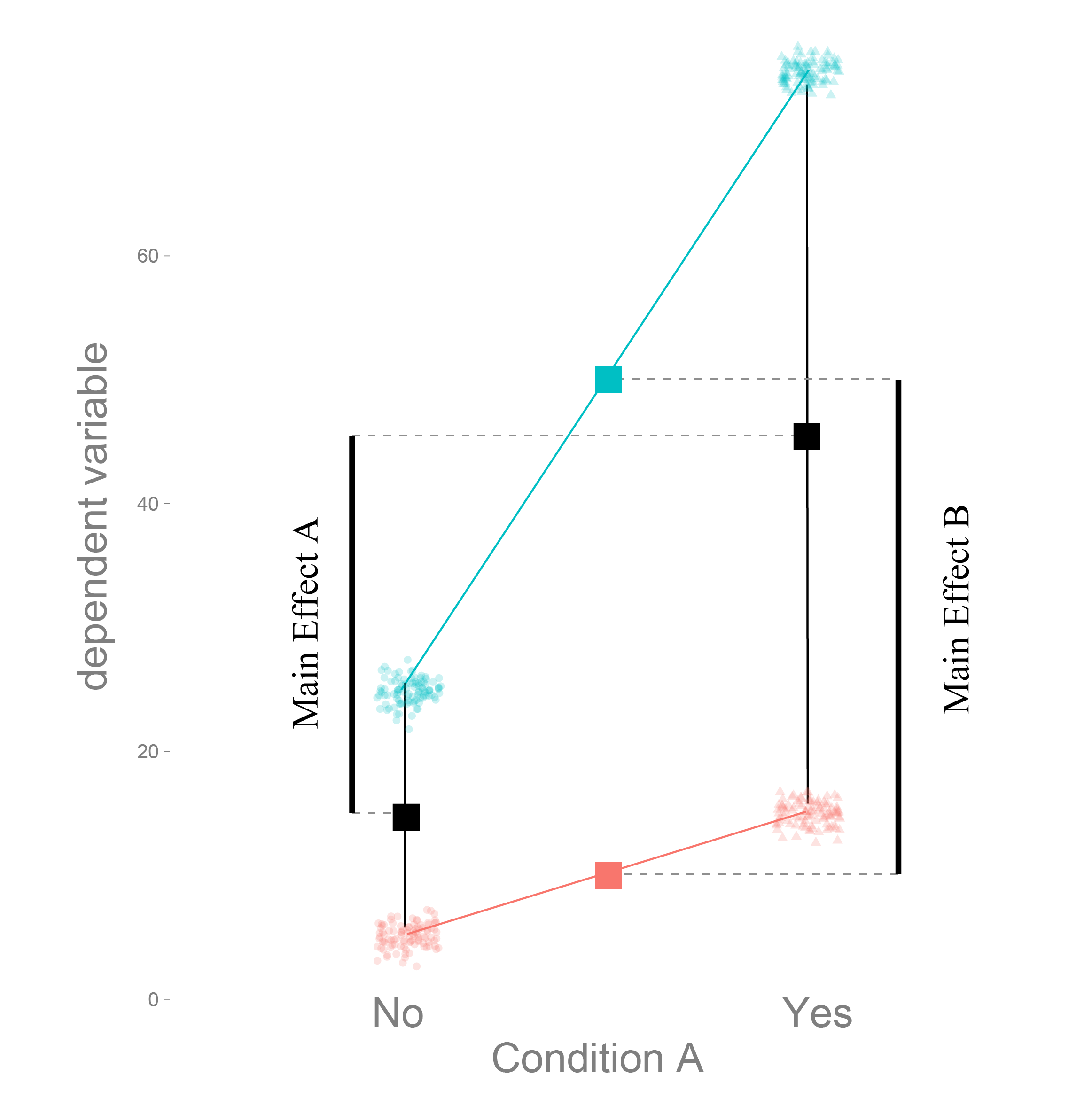
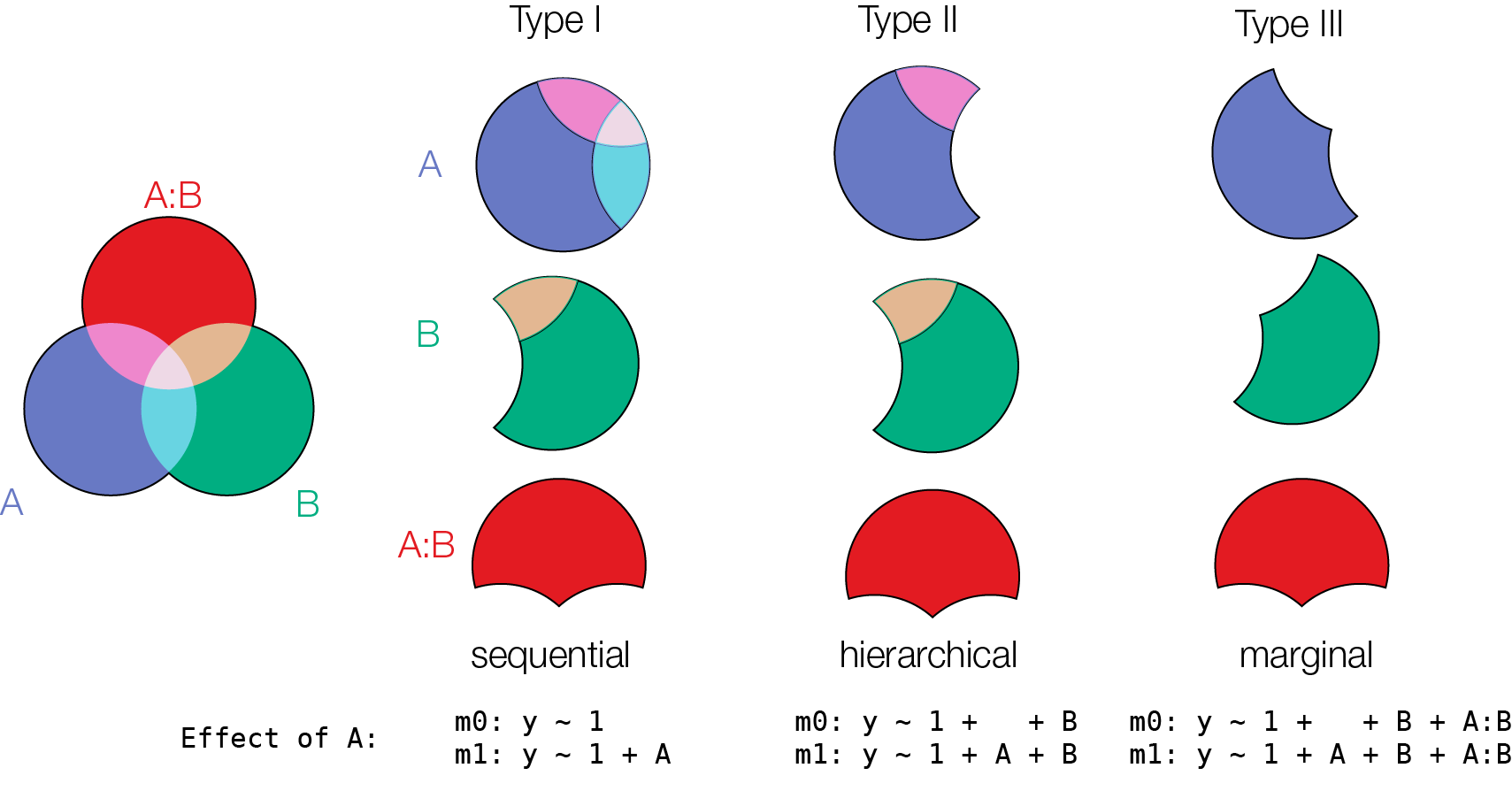
Coming back to a 2x2 design. Which order to test effects?
Model comparison does not care about recoding
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -17.39 52.44 -0.332 0.74260
## wt 47.14 13.64 3.456 0.00177 **
## am -123.33 74.03 -1.666 0.10690
## wt:am 63.84 25.08 2.545 0.01672 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: 6.266e-06##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -79.06 37.02 -2.136 0.0416 *
## wt 79.06 12.54 6.303 8.12e-07 ***
## am1 -123.33 74.03 -1.666 0.1069
## wt:am1 63.84 25.08 2.545 0.0167 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 44.99 on 28 degrees of freedom
## Multiple R-squared: 0.6111, Adjusted R-squared: 0.5694
## F-statistic: 14.66 on 3 and 28 DF, p-value: 6.266e-06Walds-T test cares (simple vs. main effects)
## Analysis of Variance Table
##
## Response: hp
## Df Sum Sq Mean Sq F value Pr(>F)
## wt 1 63238 63238 31.2413 5.555e-06 ***
## am 1 12700 12700 6.2744 0.01834 *
## wt:am 1 13111 13111 6.4774 0.01672 *
## Residuals 28 56677 2024
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Analysis of Variance Table
##
## Response: hp
## Df Sum Sq Mean Sq F value Pr(>F)
## wt 1 63238 63238 31.2413 5.555e-06 ***
## am 1 12700 12700 6.2744 0.01834 *
## wt:am 1 13111 13111 6.4774 0.01672 *
## Residuals 28 56677 2024
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model comparison does not care!
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
- Linearity of responses
- Independence
- Normality
- Equal variance
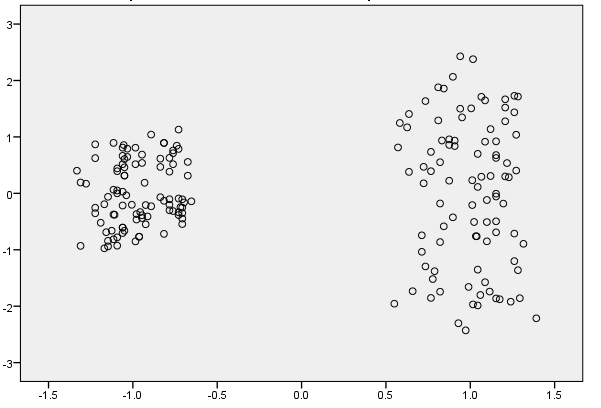
Linearity of responses
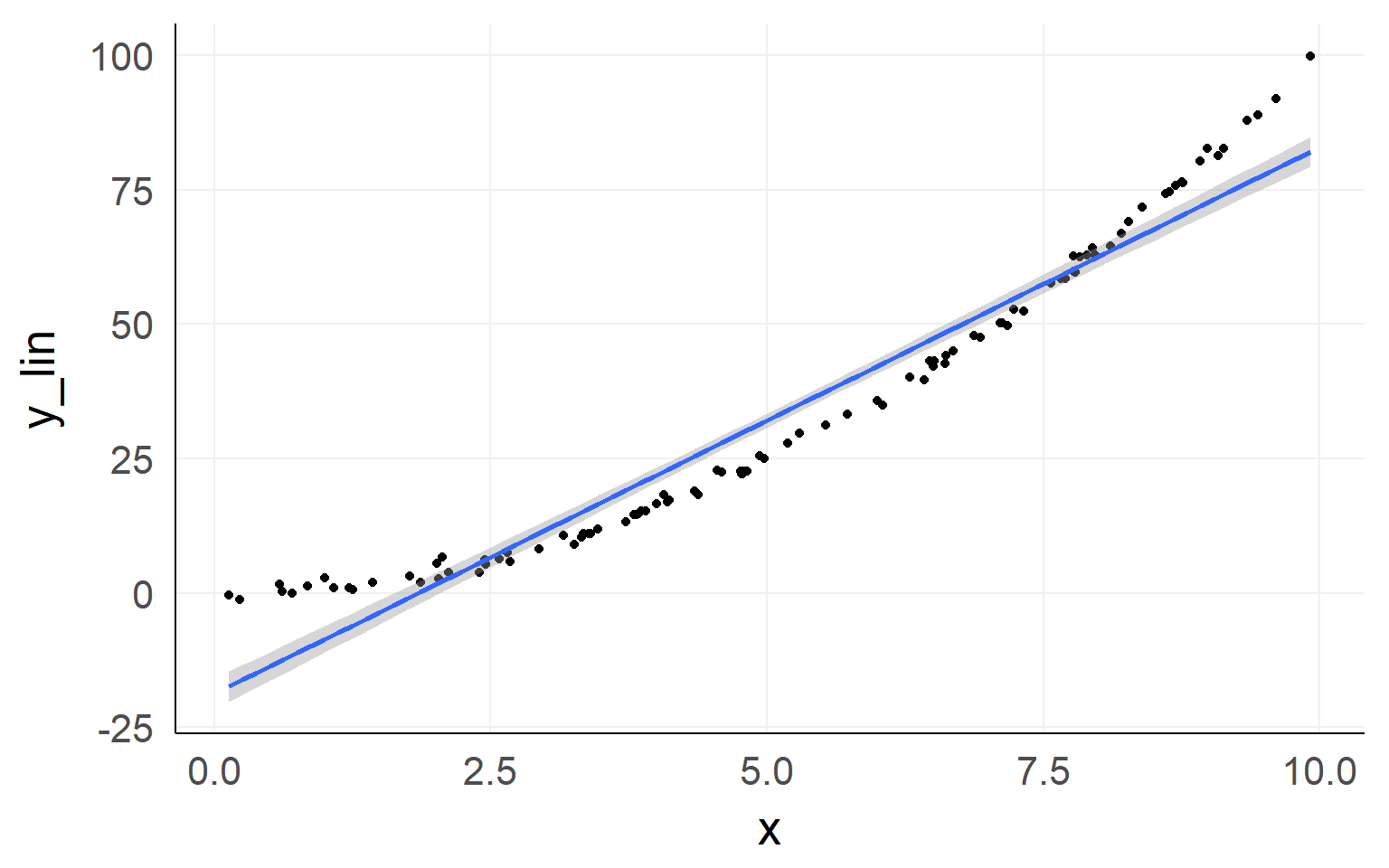
Linear response
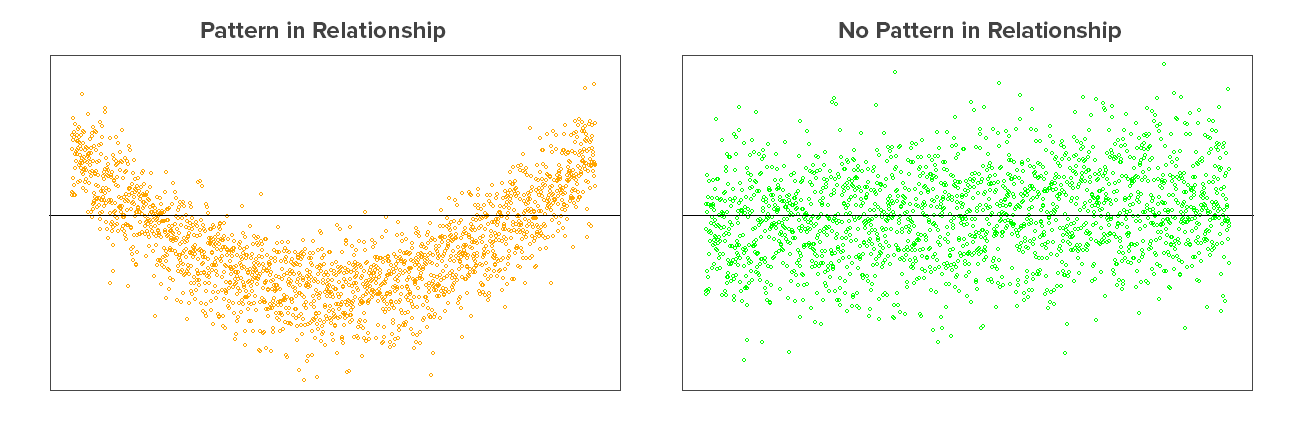
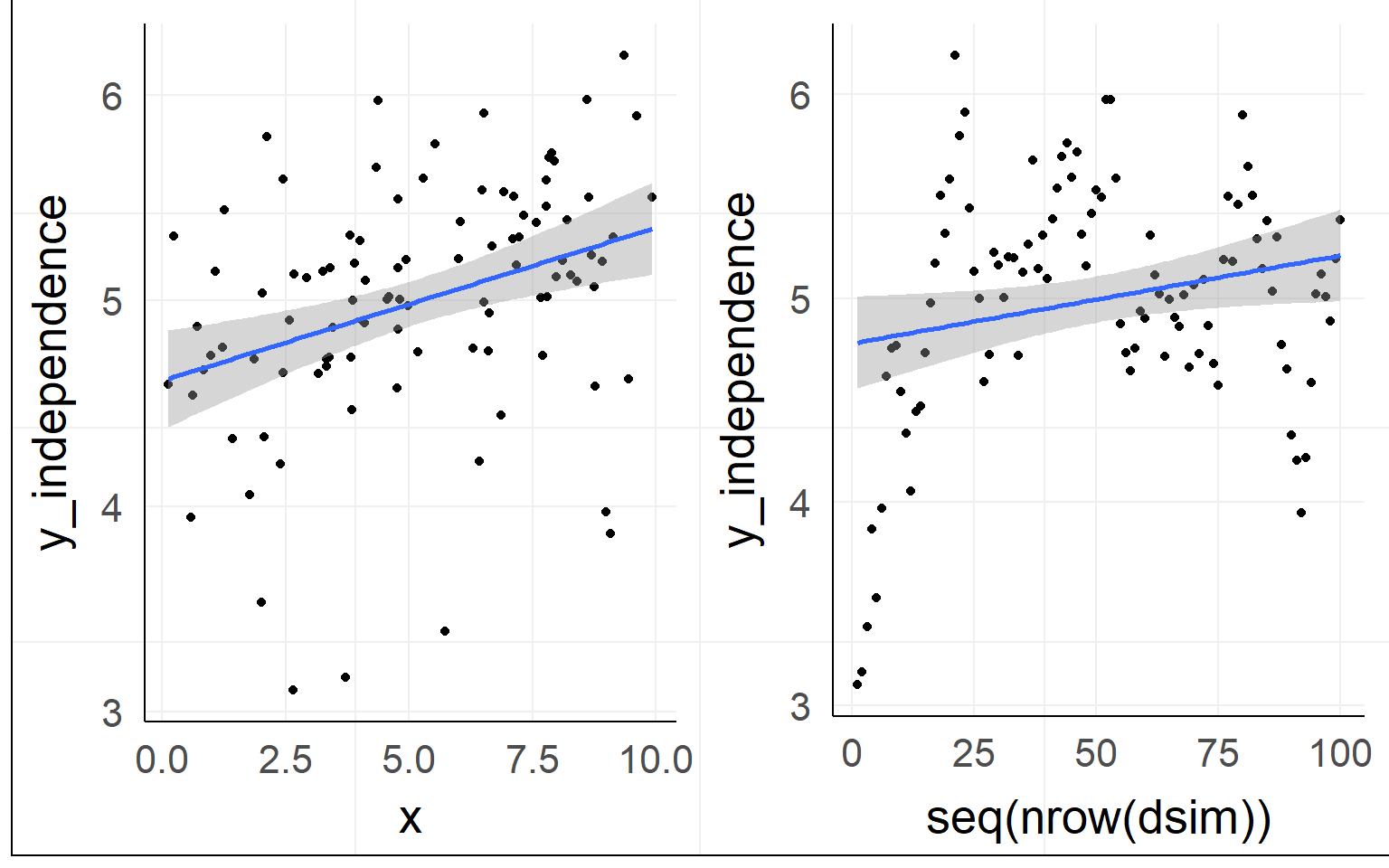
Independence of residuals
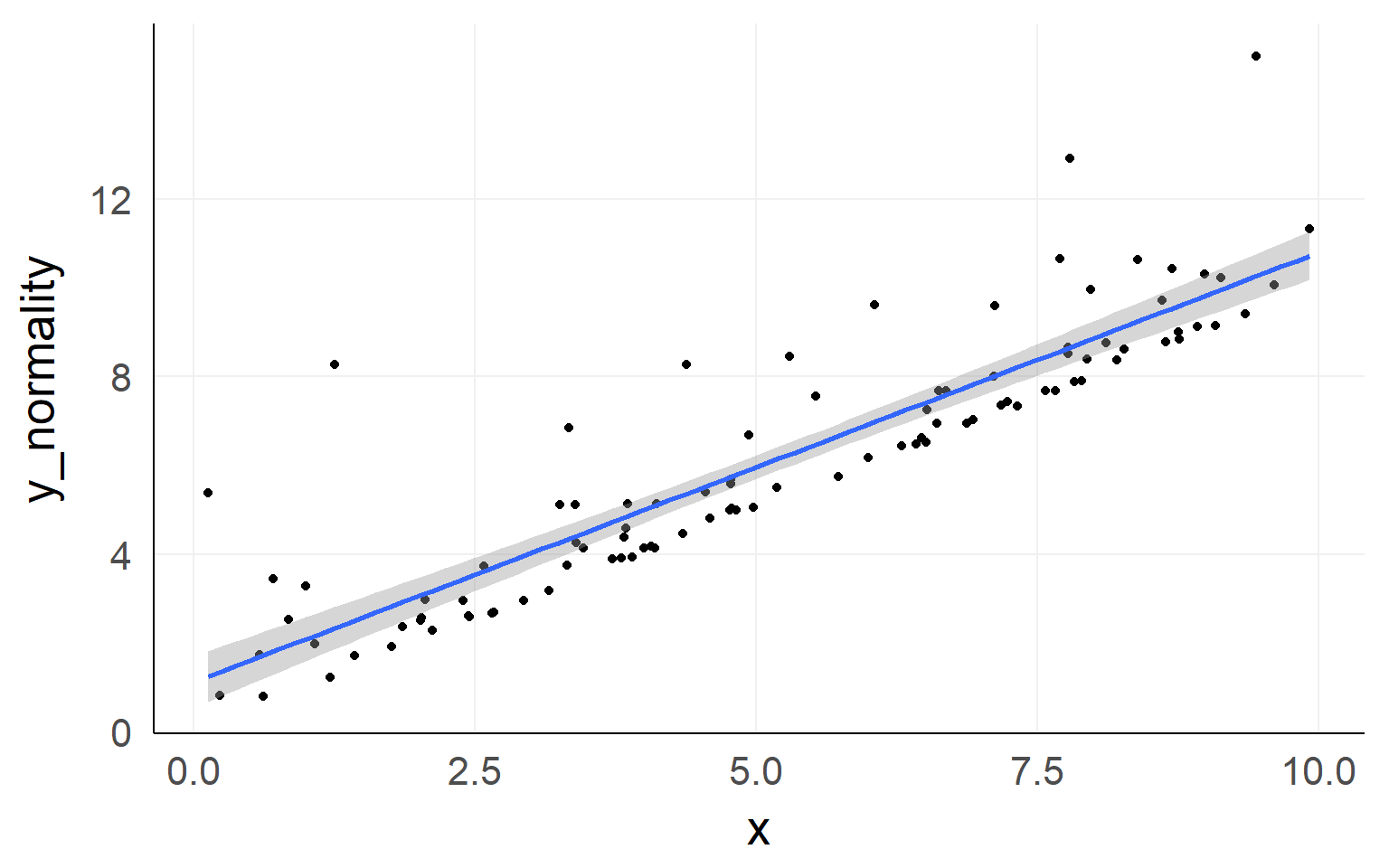
Normality of residuals
Checking Assumptions: Normality using QQplots
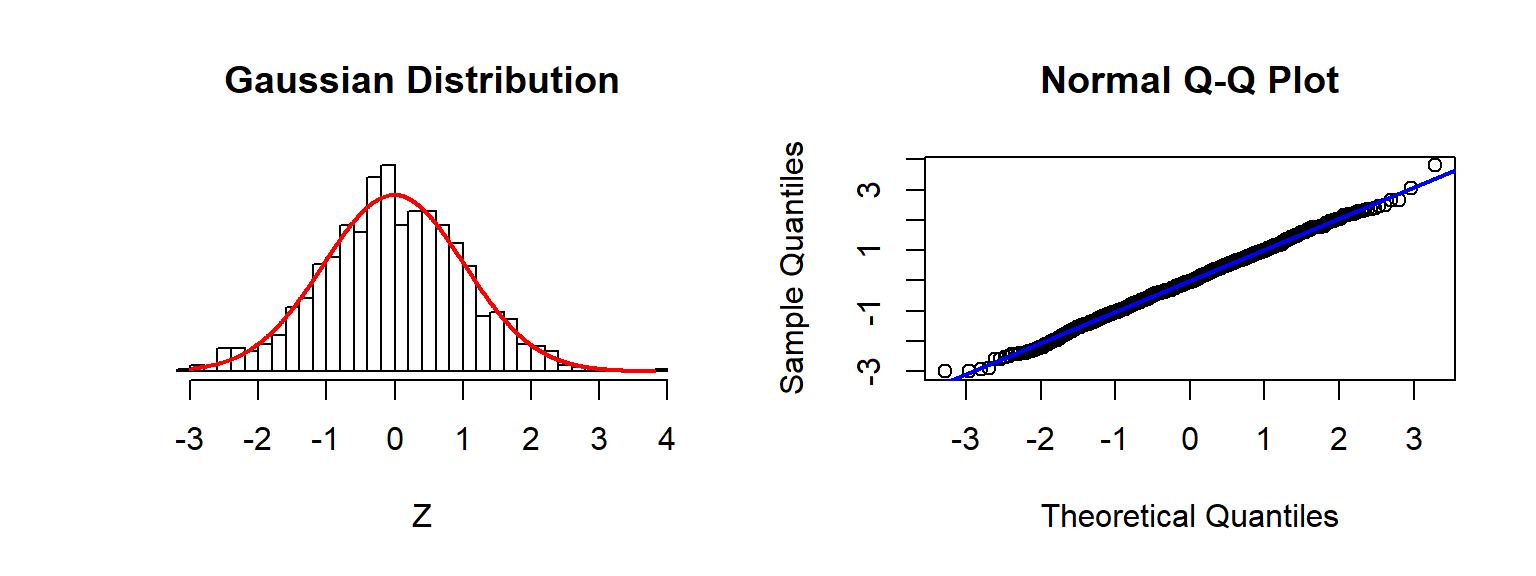
Source: Sean Kross
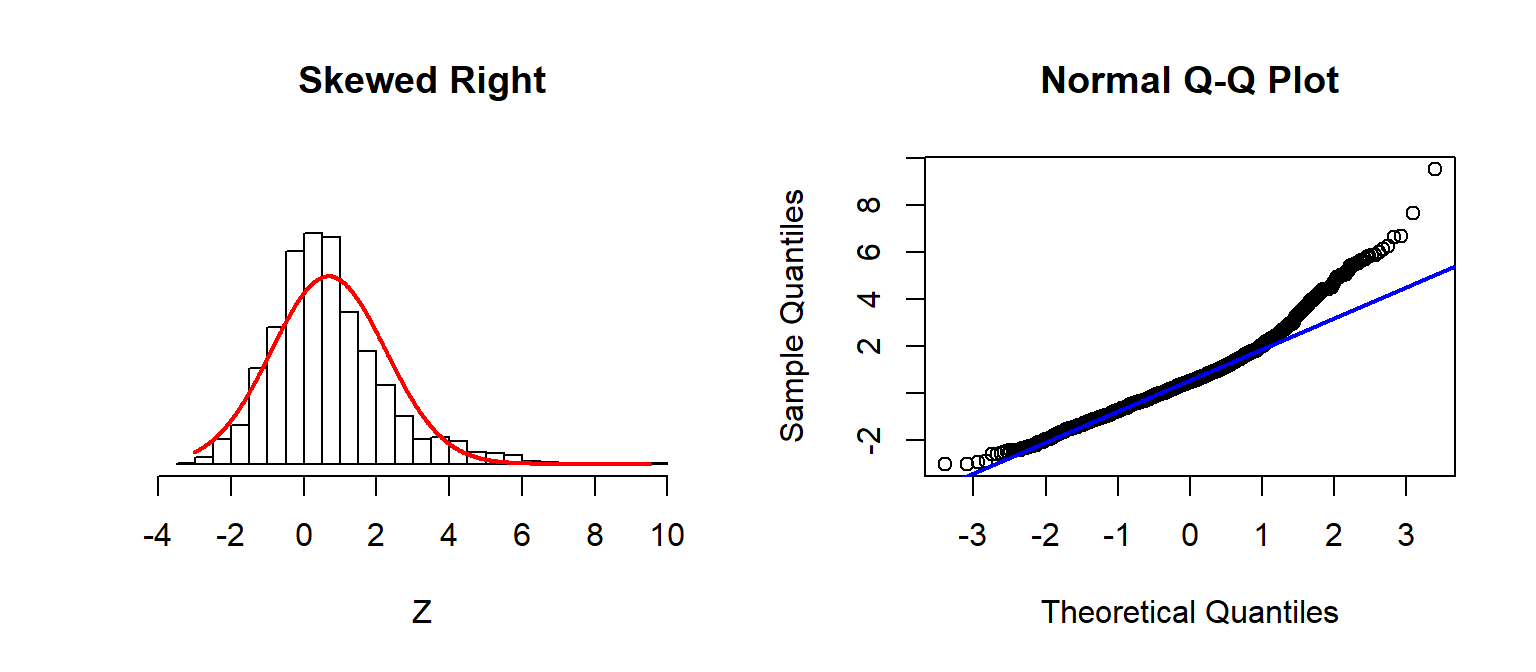
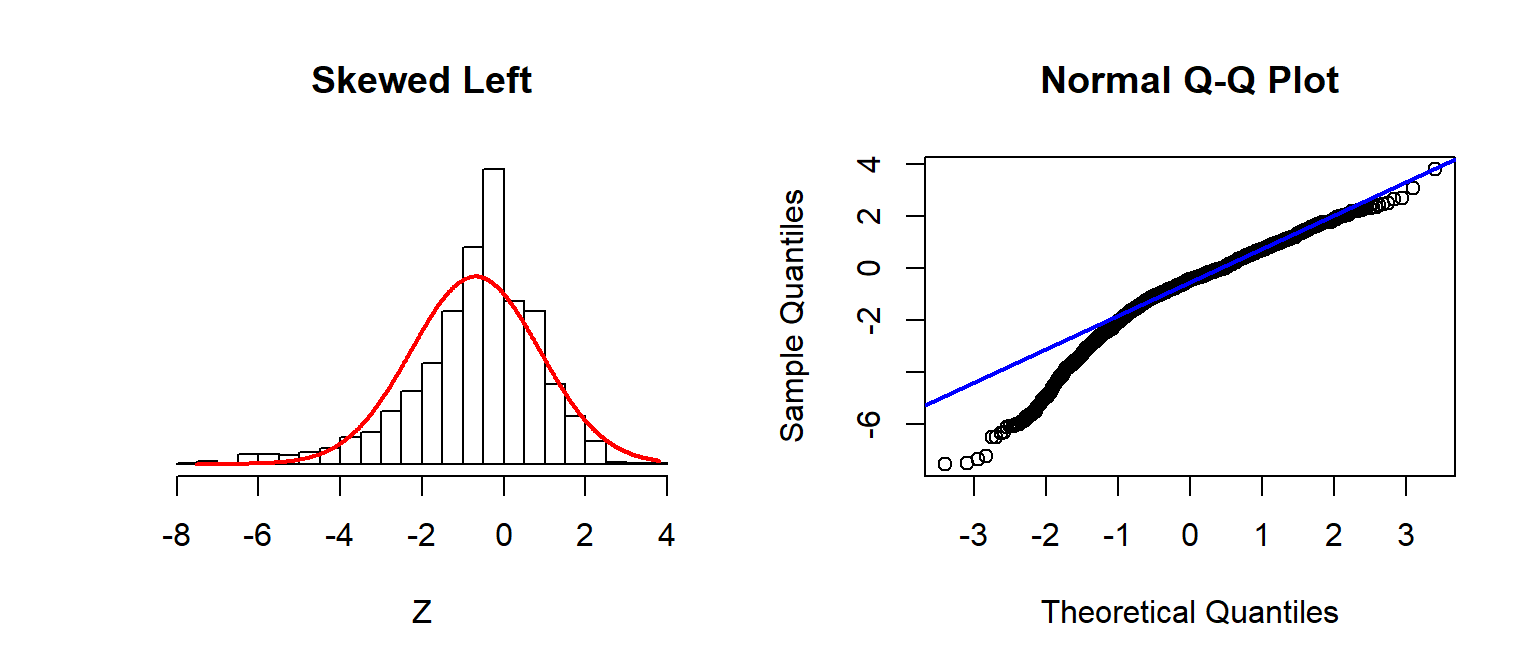
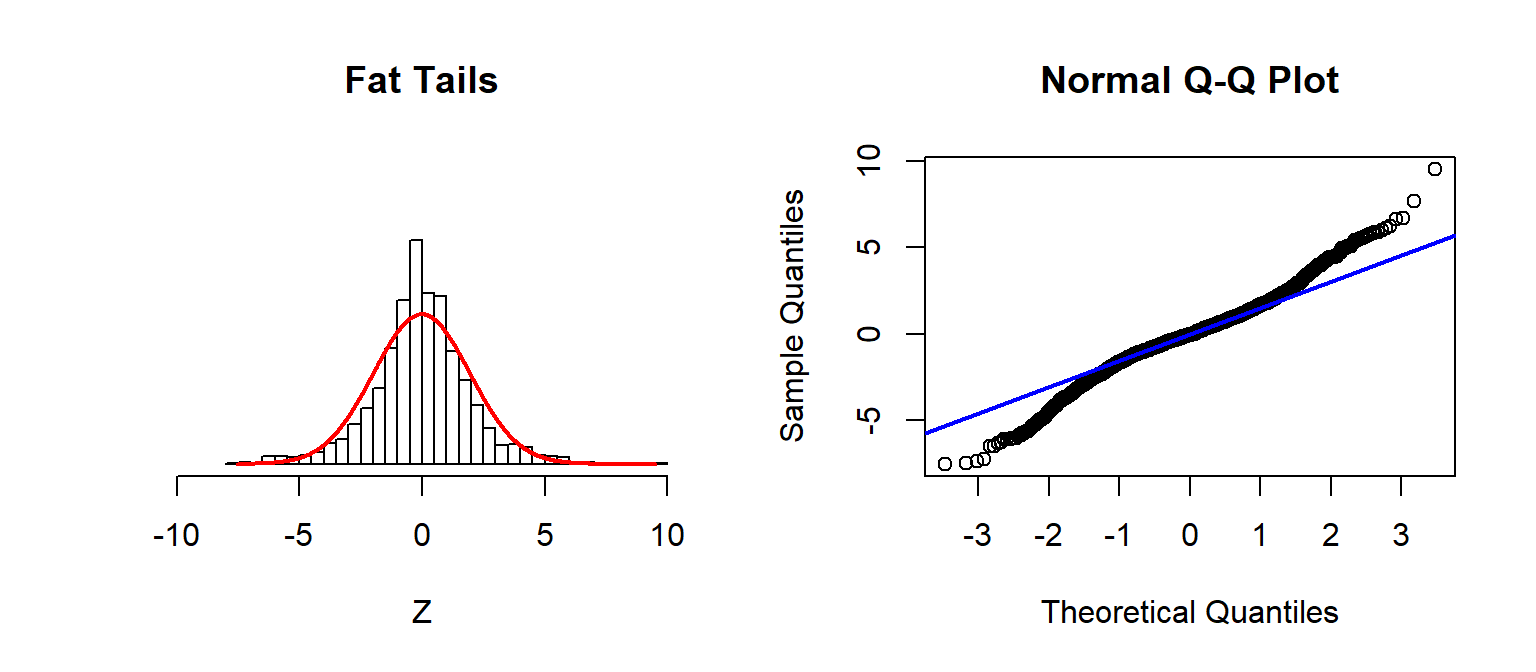
A nice trick
simulate datasets with same specifications and compare
Equal variance
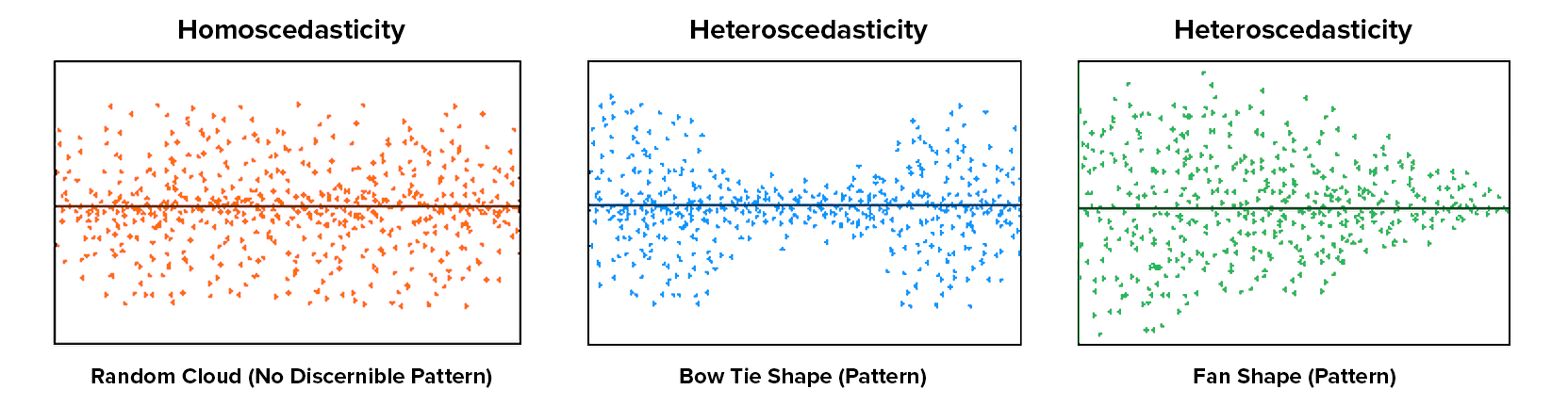
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
A bootstrap visualization
Why bootstrapping?
- Violated assumptions
- Unknown analytical + \(H_0\) distribution
Bootstrap for regression
Bootstrapping in R
##
## Call: lm(formula = read ~ math * socst, data = dSoc)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.842715 14.545210 2.602 0.00998 **
## math -0.110512 0.291634 -0.379 0.70514
## socst -0.220044 0.271754 -0.810 0.41908
## math:socst 0.011281 0.005229 2.157 0.03221 *
##
## Residual standard error: 6.96 on 196 degrees of freedom
## Multiple R-squared: 0.5461, Adjusted R-squared: 0.5392
## F-statistic: 78.61 on 3 and 196 DF, p-value: < 1e-04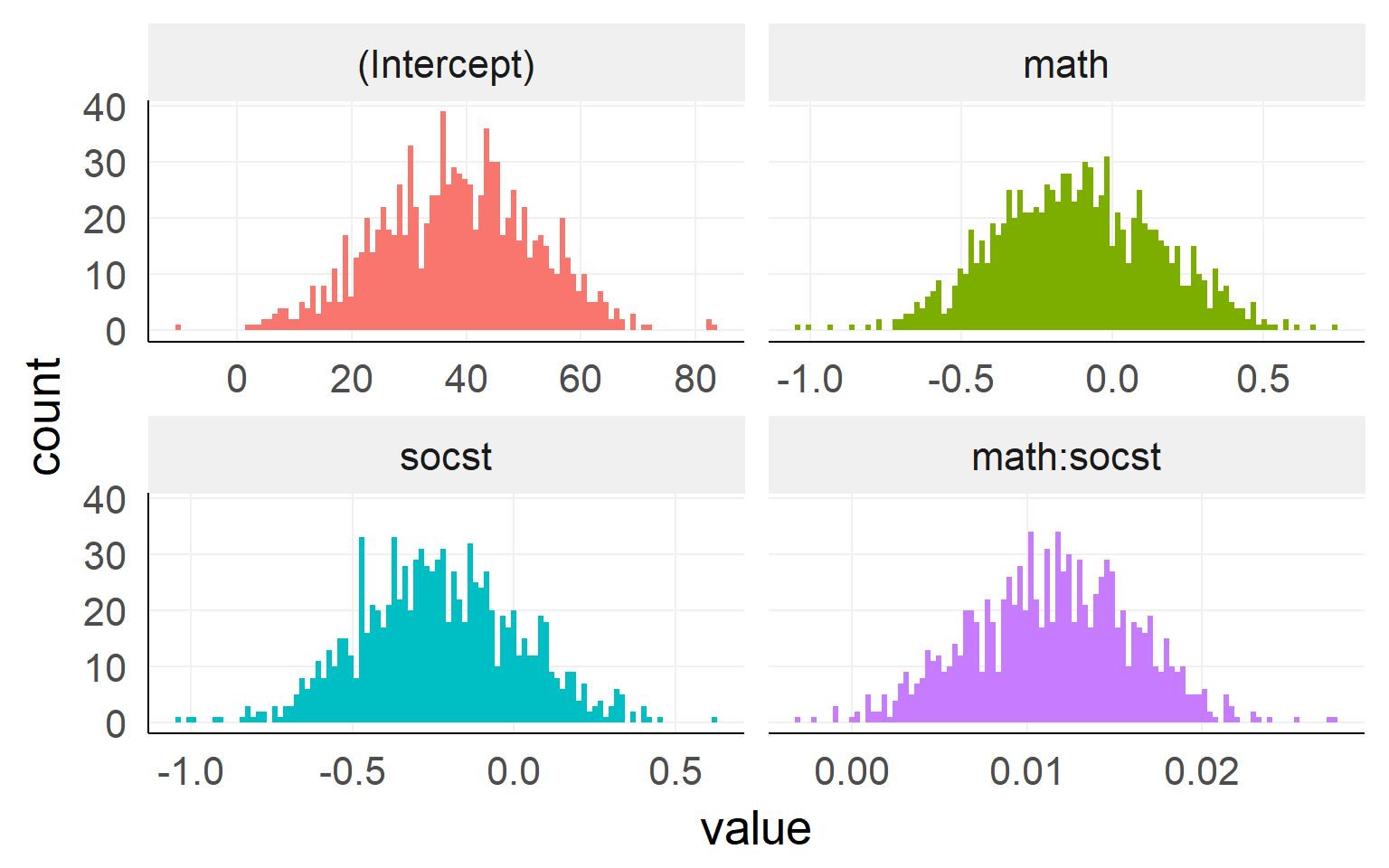
Continued
boot::boot.ci(bootres,type='bca',index=4) # 4 = which parameter from coef to get## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot::boot.ci(boot.out = bootres, type = "bca", index = 4)
##
## Intervals :
## Level BCa
## 95% ( 0.0018, 0.0196 )
## Calculations and Intervals on Original Scaleconfint(fit,parm = 'math:socst')## 2.5 % 97.5 %
## math:socst 0.0009676529 0.02159379Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
- Fisher
- Neyman-Pearson
- NHST (Null Hypothesis Testing)
- Bayes
Fisher
- p-values are a continuous measure of evidence against the \(H_0\)
- “Significant” p-values can be defined ad-hoc, i.e. what you think is enough evidence for this one test
- a sensitivity analysis (~power analysis) can be performed but is not necessary
- General idea: A single experiment should inform your decisions
Neyman-Pearson
- p-values are only used to be threshold by \(\alpha\)
- the pre-analysis fixed \(\alpha\) denotes the error-probability to receive false positives
- a power analysis is required and is part of the test
- a p-value of 0.049 and 0.001 give the same evidence (with \(\alpha=0.05\))
- General idea: Its all about long-term properties. A single experiment does not really help
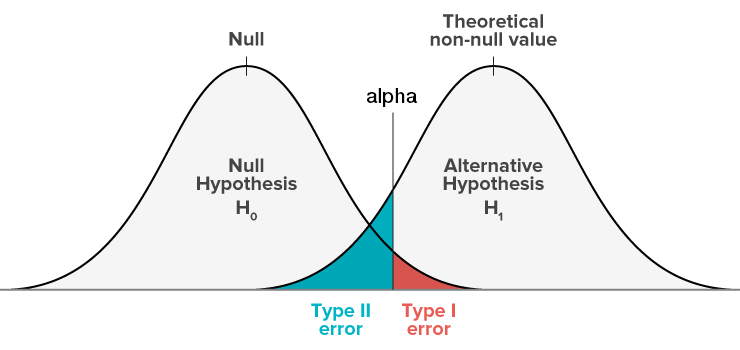
Type I vs. Type II errors
Type Errors

NHST
A dark mix between Fisher & Neyman-Pearson is currently used. This is evident by calculating a p-value, p-values below \(\alpha\) are significant (NP). But exact p-values are still reported.
This is a very popular mix - but is not consistent. Either you want to accept / reject a finding (and be correct on the long run) or you want to identify how much evidence you have from your sample (and act according to how much evidence you have).
Bayes
- parameter estimates (combined with the apropriate aka fully informed prior) reflect the probability of the true parameter being this value
- P-Values are of no use - one can contrast two opposing hypotheses directly (e.g. model-selection)
- usually not interested in testing hypotheses, but more on estimating likely ranges of parameters
An intuition on the difference between Bayes & Frequentist
- Frequentist:
- All about the sampling distribution
- probabilities are frequencies of (hypothetical) outcomes
- Hypothetical Population and experiments (=> sampling distribution)
- A population-parameter has a true value
- “top down”
- Bayesian:
- All about the (subjective*) probabilities of parameters
- probabilities are plausibilities/certainties
- population-parameters are uncertain
- “bottom up”
They can result in exactly the same numbers. But interpretation vastly different!
- sometimes called subjective because of subjective choice of priors
Be both if you can!
Come join our Seminar: “Statistical Rethinking Reading Club” next semester
“This is a rare and valuable book that combines readable explanations, computer code, and active learning.” —Andrew Gelman, Columbia University
“…an impressive book that I do not hesitate recommending for prospective data analysts and applied statisticians!” —Christian Robert, Université Paris-Dauphine (review)
“A pedagogical masterpiece…” —Rasmus Bååth, Lund University
“The content of this book has been developed over a decade+ of McElreath’s teaching and mentoring of graduate students, post docs, and other colleagues, and it really shows.” —Brian Wood, Yale
“…omg suddenly everything makes sense…” —Ecstatic anonymous reader
Overview
- Warmup
- Why statistics
- do it yourself statistics
- Linear Regression
- Multiple Regression
- Categorical Variables
- Interactions and the famous 2x2 design
- Inference
- Asumptions
- Bootstrapping
- Four ways of statistics
- Equivalence of traditional tests
Correlation
\[r = \frac{cov_{XY}}{\sigma_X\sigma_Y}\] \[ Y = \beta_0 + X\beta_1\] \[ r = \beta_1\frac{\sigma_X}{\sigma_Y}\]
Alternative: standardize both Y & X (e.g. \(Y^* = \frac{Y}{\sigma_Y}\)) before fitting the regression, you will receive correlations
t-test
Test for two groups: \(t = \frac{\hat \mu_1 - \hat \mu_2}{\sqrt{SE_1^2 + SE_2^2}}\)
t.test(data$DriversKilled[data$law==0],data$DriversKilled[data$law==1],var.equal = T)##
## Two Sample t-test
##
## data: data$DriversKilled[data$law == 0] and data$DriversKilled[data$law == 1]
## t = 4.7942, df = 190, p-value = 3.288e-06
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 15.07239 36.14552
## sample estimates:
## mean of x mean of y
## 125.8698 100.2609print(summary(lm(data=data,DriversKilled~law)),concise=T)##
## Call: lm(formula = DriversKilled ~ law, data = data)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 125.870 1.849 68.082 <1e-04 ***
## law -25.609 5.342 -4.794 <1e-04 ***
##
## Residual standard error: 24.03 on 190 degrees of freedom
## Multiple R-squared: 0.1079, Adjusted R-squared: 0.1032
## F-statistic: 22.98 on 1 and 190 DF, p-value: < 1e-04ANOVA
d = data.frame(datasets::mtcars)
d$gear = factor(d$gear)
summary(aov(hp~gear,data=d))## Df Sum Sq Mean Sq F value Pr(>F)
## gear 2 64213 32106 11.42 0.00022 ***
## Residuals 29 81514 2811
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1l1 = lm(hp~1+gear,data=d)
l0 = lm(hp~1,data=d)
anova(l1,l0)## Analysis of Variance Table
##
## Model 1: hp ~ 1 + gear
## Model 2: hp ~ 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 29 81514
## 2 31 145727 -2 -64213 11.422 0.0002196 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ANCOVA
summary(aov(price~factor(bedrooms)+reviews,dair[1:800,]))## Df Sum Sq Mean Sq F value Pr(>F)
## factor(bedrooms) 8 7797765 974721 26.238 <2e-16 ***
## reviews 1 28260 28260 0.761 0.383
## Residuals 790 29347410 37149
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1l1 = lm(price~1+factor(bedrooms)+reviews,data=dair[1:800,])
l0 = lm(price~1+factor(bedrooms),data=dair[1:800,])
anova(l0,l1)## Analysis of Variance Table
##
## Model 1: price ~ 1 + factor(bedrooms)
## Model 2: price ~ 1 + factor(bedrooms) + reviews
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 791 29375670
## 2 790 29347410 1 28260 0.7607 0.3834recommendations
I like these books: - Statistical Rethinking - (more math) Advanced Data Analysis from an elemental point view (Cosma Shalizi)
I like these webpages: https://www.flutterbys.com.au/stats/
And thats it!
