How to use bimodal priors for bayesian data analysis in STAN

I tried adding a bi-modal prior in STAN for a homework exercise on Bayesian Data Analysis. At first, I thought this could work:
“`STAN
model{
mu ~ normal(-0.5,0.3) + normal(0.5,0.3);
}
“`
But it doesn’t. I had to dig deeper and I thought I could simply add multiple times to the log-posterior due to a sideremark of Bob Carpenter:

“`STAN
target += normal_lpdf(mu|.5,0.3);
target += normal_lpdf(mu|-.5,0.3);
“`
Which also does not work. Finally, the solution is akin to the mixture model in the STAN manual:

“`STAN
target += log_sum_exp(normal_lpdf(mu|.5,0.3),normal_lpdf(mu|-.5,0.3));
“`

This results in beautiful bi-modal priors:

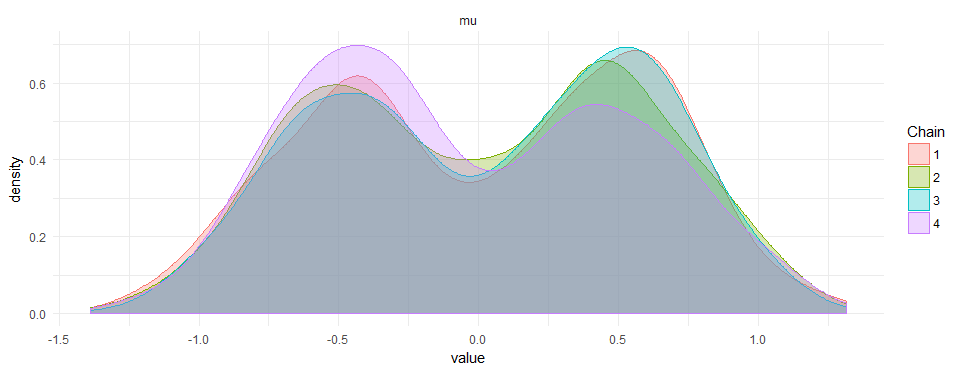
I did not find anything on google or the manual of how to do this. If there is a smarter way to do it, please leave a comment.

“`R

library(rstan)

model <- " data { } parameters { real mu; } transformed parameters { } model { //mu ~ normal(10,1); //mu ~ normal(-10,1); target += log_sum_exp(normal_lpdf(mu|-.5,.3),normal_lpdf(mu|.5,.3)); }" samples <- stan(model_code=model, iter=2000, chains=4, thin=1, # seed=123 # Setting seed; Default is random seed ) ggmcmc::ggs_density(ggmcmc::ggs(samples))+theme_minimal() ```