Independent Component
Analysis
An interactive exploration
Teatime by Benedikt Ehinger
The problem
- \[ \begin{aligned} A &=& sin(2*\theta) \\B &=& sin(\theta) \end{aligned}\]
-
\[ \begin{aligned} C &=& 2*A &+ 0.3*B \\D &=& 2.73*A &+ 2.41*B \end{aligned}\]
- Undo the Stretching
-
Undo the Rotation
More formal
(and a different example)
- \( x = As \) with \( A = \left(\begin{align}\begin{array}{lr}2 & 0.3 \\ 2.73 & 2.41 \end{array}\end{align}\right) \)
- \[ \text{cov}(C,D) \overset{!}{=} I \]
- \[ A^{-1}x = s\]
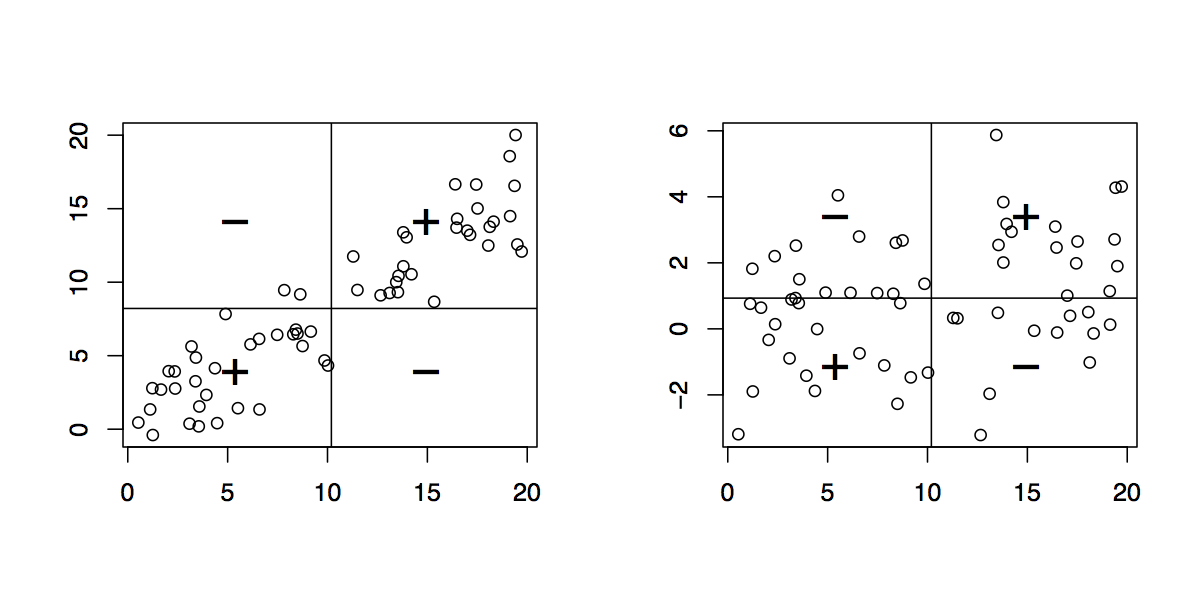
Excourse: How does PCA solve this problem?
- \[ \begin{aligned} A &=& sin(2*\theta) \\B &=& sin(\theta) \end{aligned}\]
- \[ \begin{aligned} C &=& 2*A &+ 0.3*B \\D &=& 2.73*A &+ 2.41*B \end{aligned}\]
- Undo the Stretching
- Undo the Rotation
Two Popular Ways to solve the IC Problem
Mutual Information
Mutual information is the amount of information that you get about the random variable X when you already know Y. It is a measure of shared information.
If X and Y are independent, mutual information is 0.
Therefore by minimizing the mutual information between mixed signals, we make them independent
Maximizing Non-Gaussianity
Central Limit Theorem: Mixtures of variables are 'more' normaly distributed. Therefore independent signals are (usually) less normal!
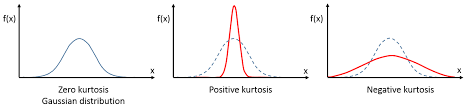
Maximize the non-gaussianity by e.g. maximizing kurtosis, or maximizing negentropy (fastICA)
Main Limitations
Small Reminder:
\[ x = As \]x = mixed Signal, A = Mixing Matrix, s = sources
\[ A = WS \]W = weight Matrix, S = sphering Matrix
Order of Sources
Sources are ordered 'randomly'. Every permutation P of s \[ s_{p} = Ps \] can be matched by a permuted mixingmatrix \[ A_{p} = AP^{-1}\] resulting in \[ x_{p} = A_{p}s_{p} = AP^{-1}Ps = As = x\]Scaling of Sources
Arbitray scaled sources \(s_{k} = k*s\): \[ x = As_{k} \] allows us to be matched with \[A_{k} = \frac{1}{k}A \] resulting in \[ x = \frac{1}{k}As_{k} = \frac{k}{k}As \] this is also true for the sign (\(k = -1\))Gaussian Variables
A mixture of two gaussian variables is point symmetric, it generally cannot be separated.
Maximally one gaussian variable can be separated from other non-gaussian sources using ICA
Orthogonality
In difference to PCA, the complete mixing matrix \( A \) is usually not orthogonal. The weight matrix W usually is, if whitening (with S) is performed.
Assumptions
- Each source is statistical independent from the others
- The mixing matrix is square and of full rank, i.e. there must be the same number of signals to sources and they must be linearly independent from each other
- There is no external noise - the model is noise free
- The data are centered
- There is maximally one gaussian source.
Thank you for your attention
References:
PDF: Tutorial on ICA - Dominic Langlois, Sylvain Chartier, and Dominique Gosselin
HTML: ICA for dummies - Arnould Delorme
HTML: (fast)ICA Tutorial - Aapo Hyvärinen
An intuitive Tutorial of ICA
www.benediktehinger.de/ica - webpage to interactively explore ICA