Mixed Models / Hierarchical Models
Benedikt Ehinger
March 22nd, 2018
Slides & my Presentation style
Click this link to add notes to the slides
this adds ?showNotes=true to the file
You can download the pdf or print them yourself:
click this link for pdf printable (use google chrome)
click this link for pdf printable + notes
HTML is best viewed in chrome
Overview
- Repeated measures
- An example to guide you through the steps
- The mixed model
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
Repeated measures
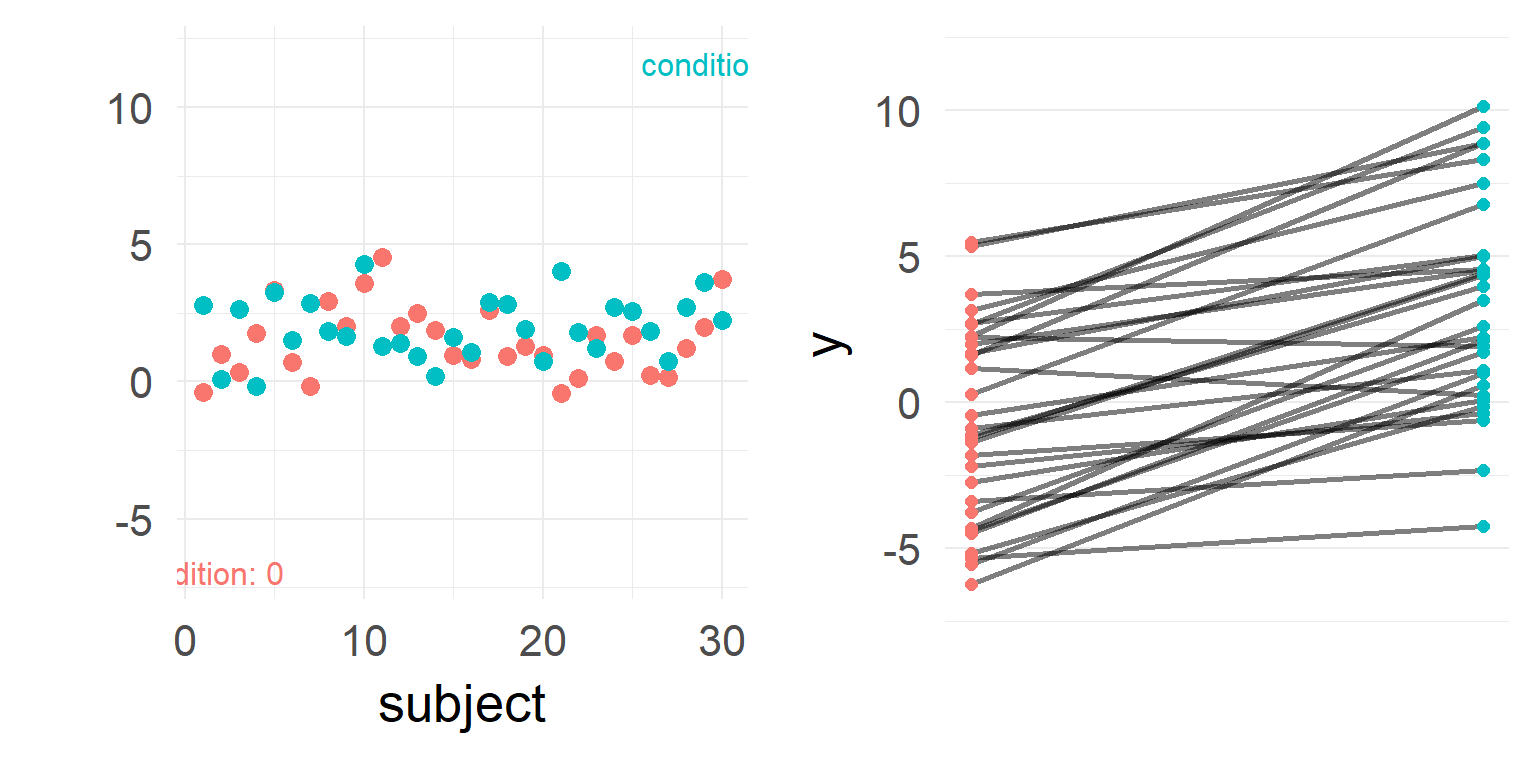
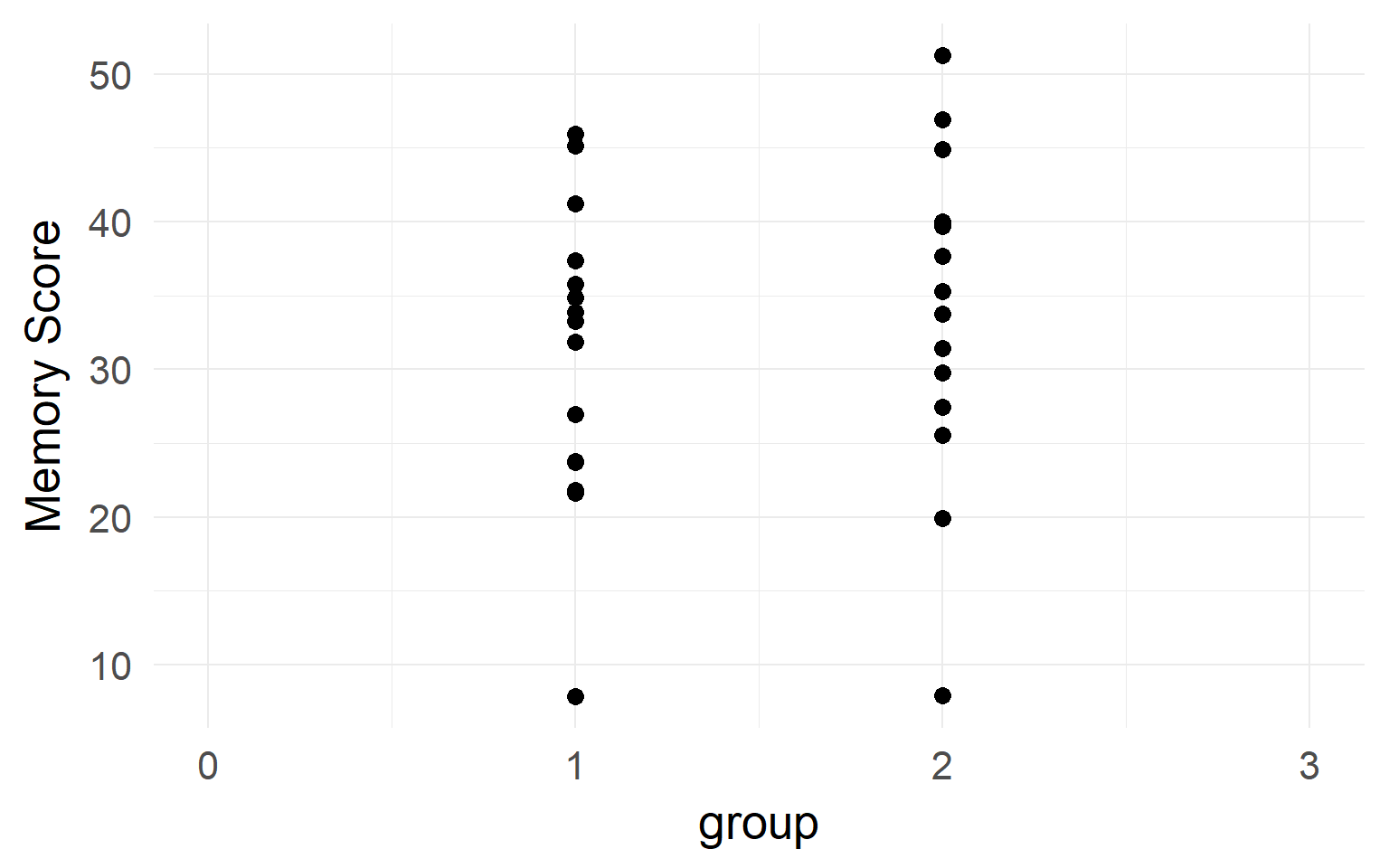 It looks like there is no difference between groups?
It looks like there is no difference between groups?
But what if we have data from within the same subjects?
Repeated measures
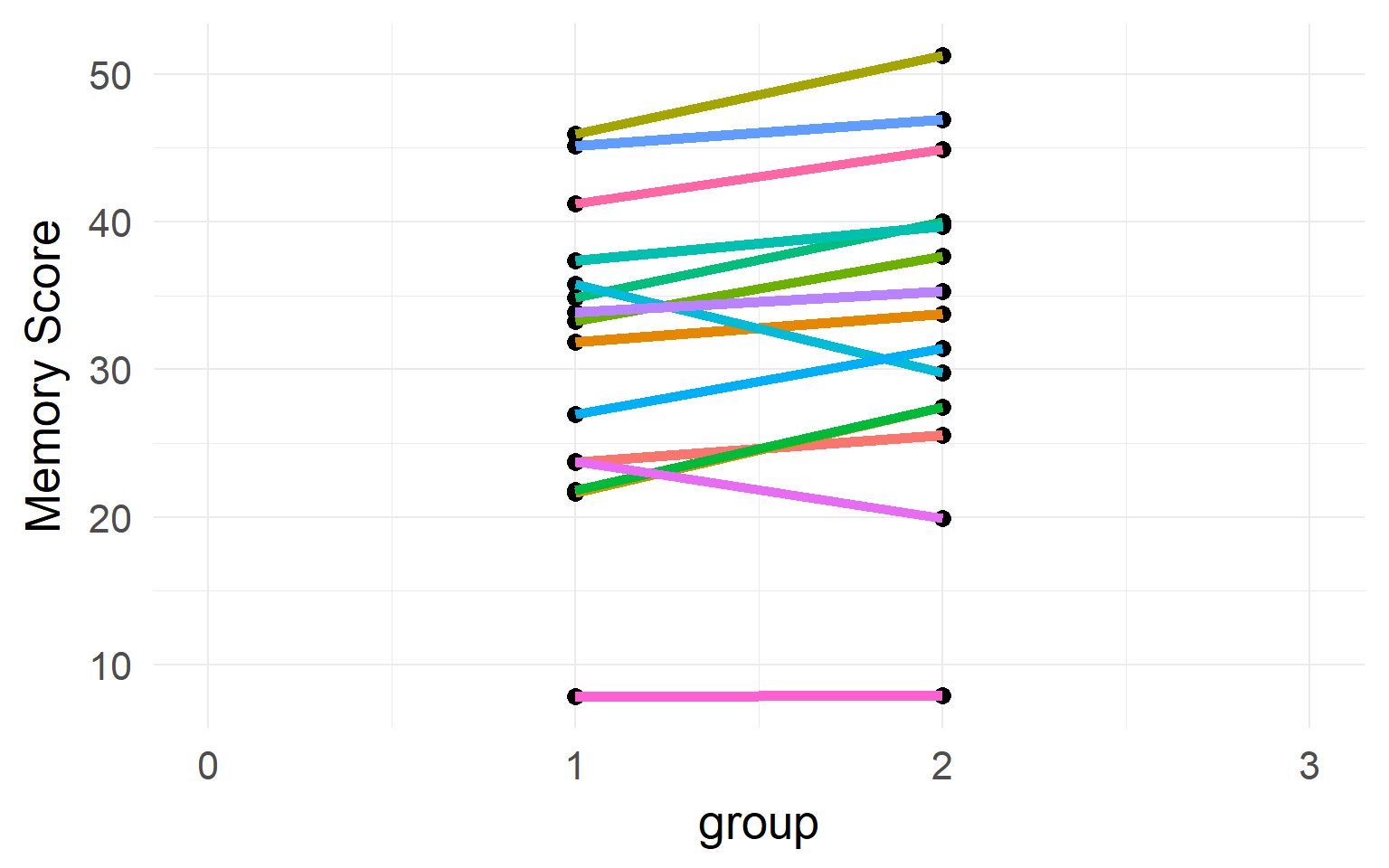
Individual differences
 Between-Subject variability can be removed by repeated measures.
Between-Subject variability can be removed by repeated measures.
Never analyze repeated measures data without taking repeated measures into account (Disaggregation, Pseudoreplication)
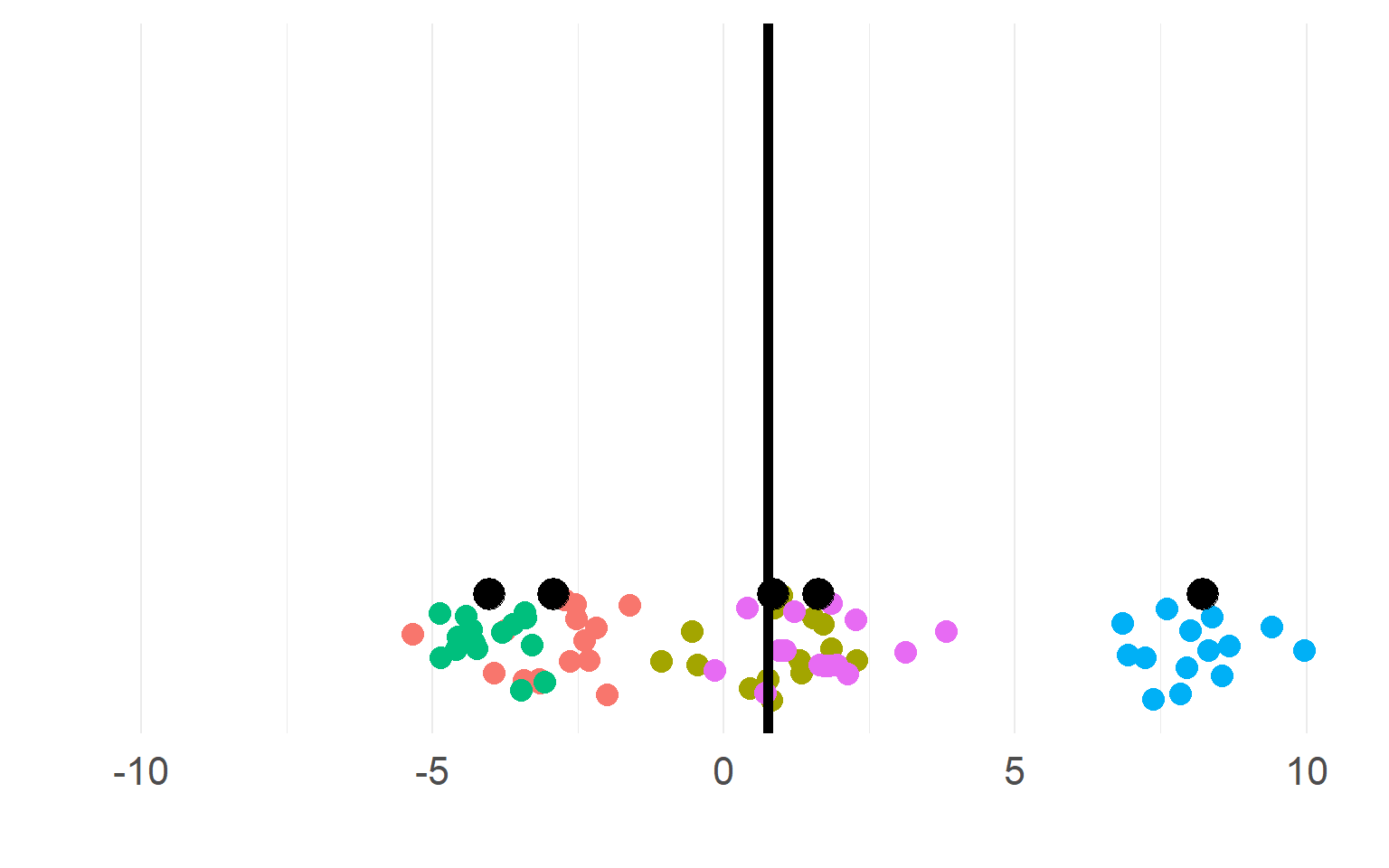
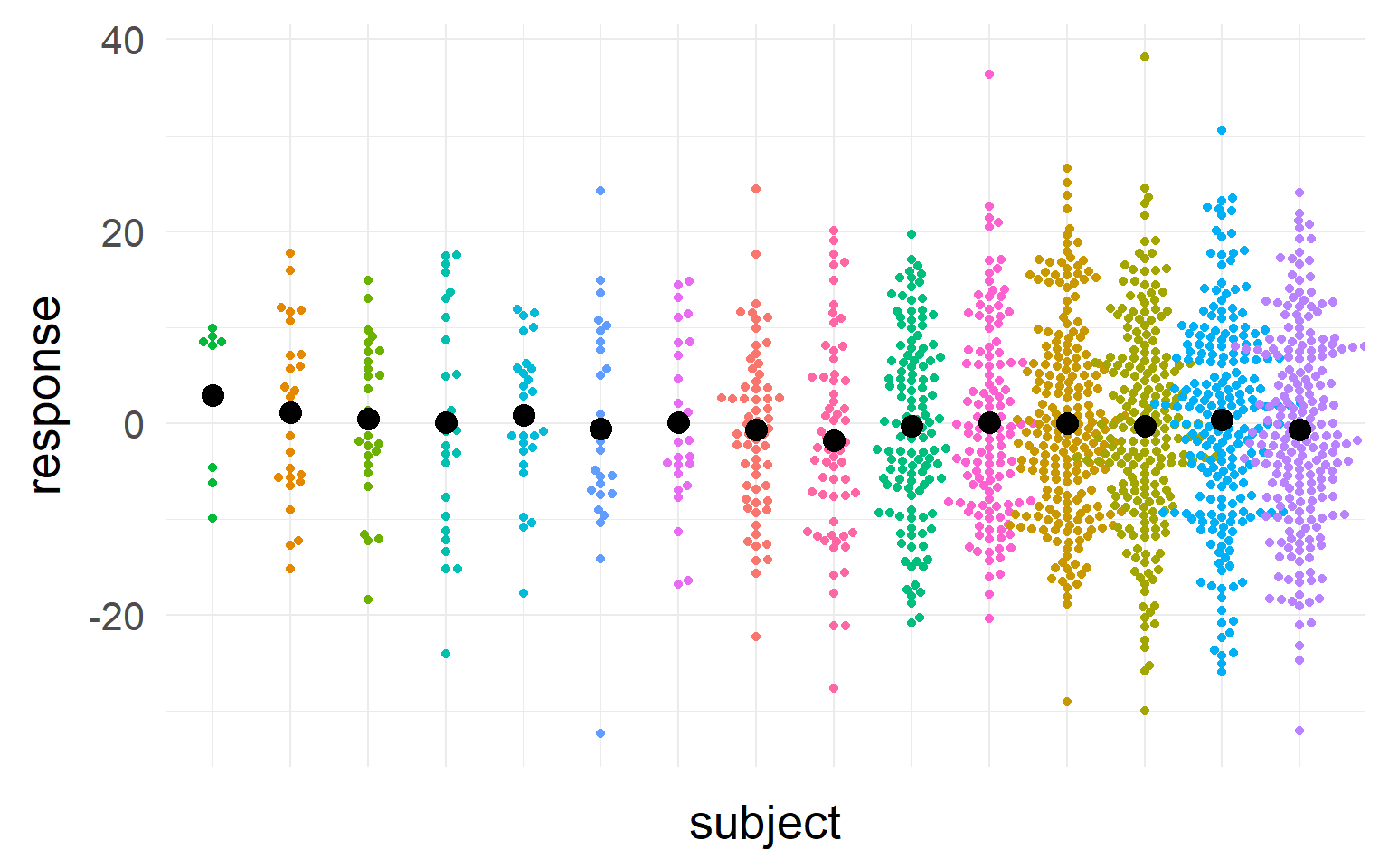
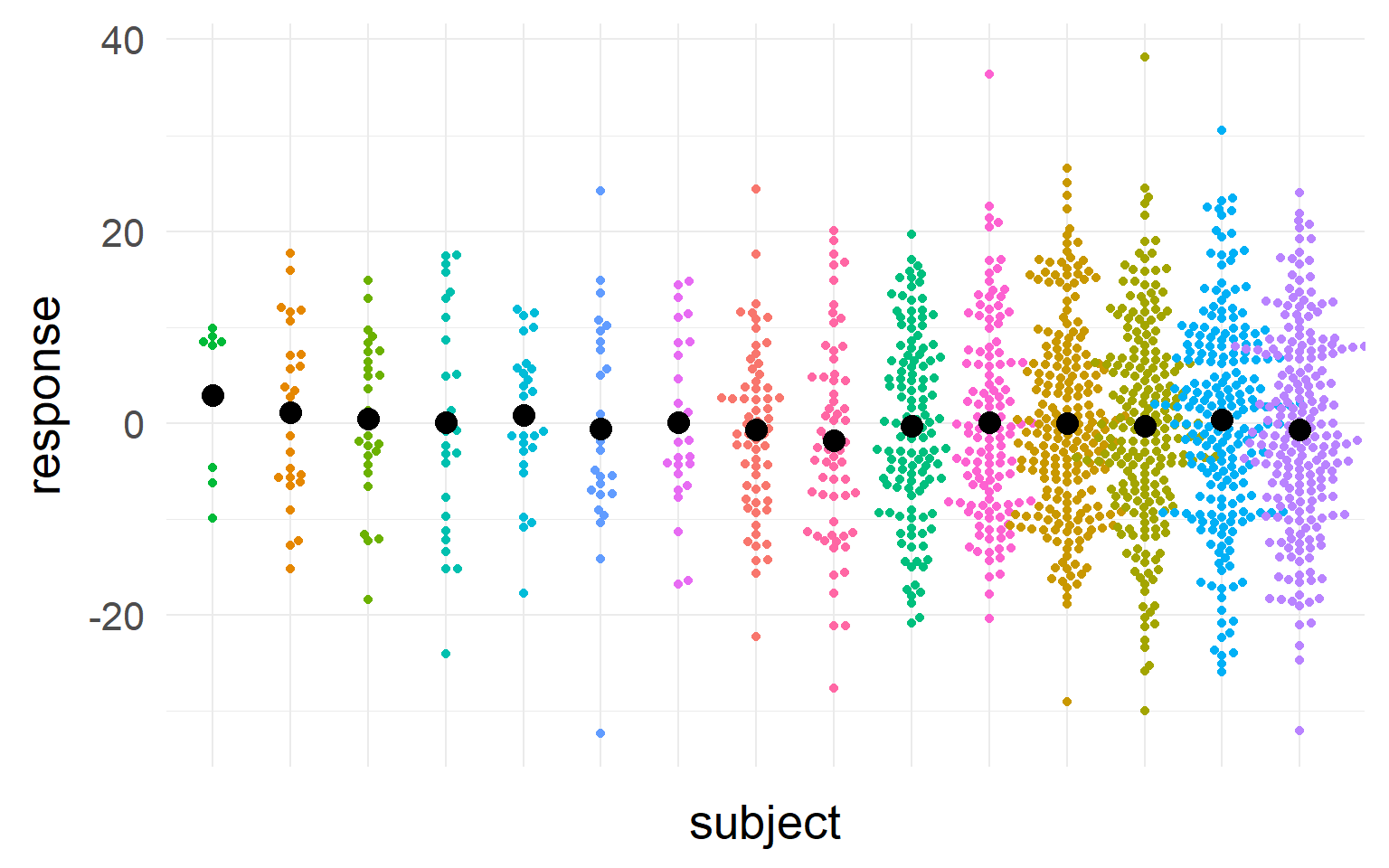
Accouting for repeated measures?
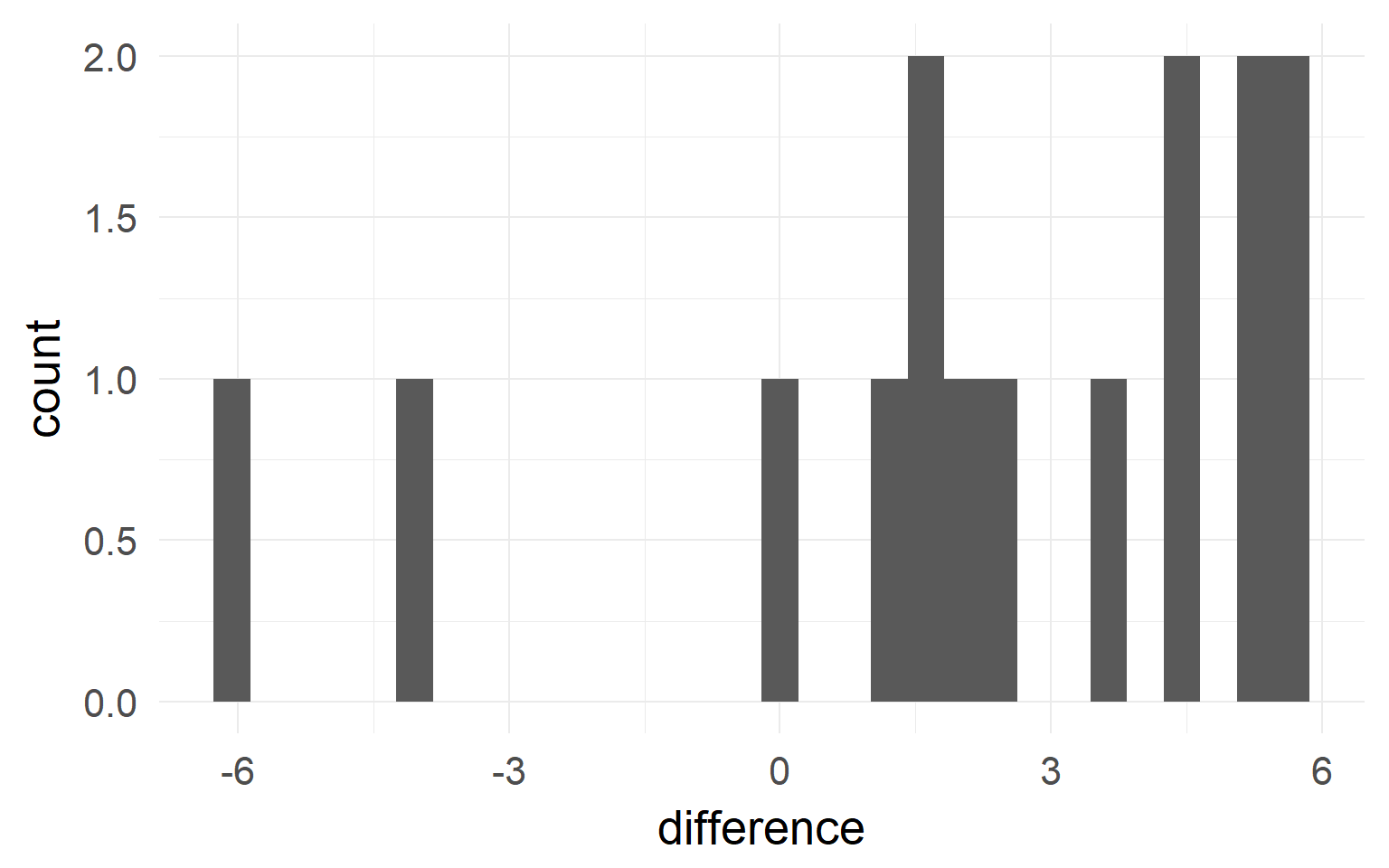
 Black = mean of the subject.
Black = mean of the subject.
\(n_S=5\) subjects
Sampling distributions
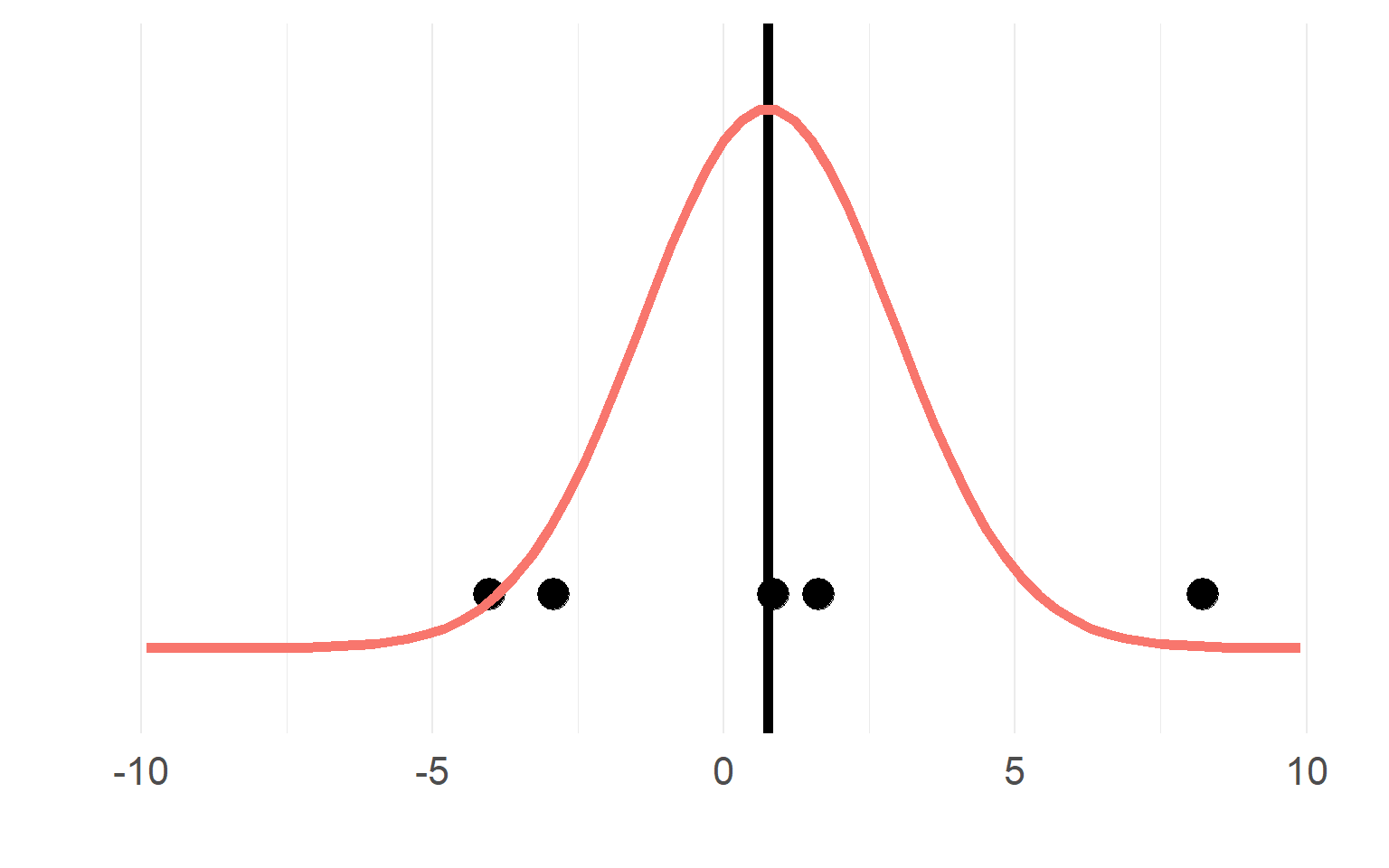
Multiple trials per subject
 with \(n_T =15\) trials
with \(n_T =15\) trials
Sampling distributions
 This sampling distribution reflects these exact 5 subjects. But does not generalize!
This sampling distribution reflects these exact 5 subjects. But does not generalize!
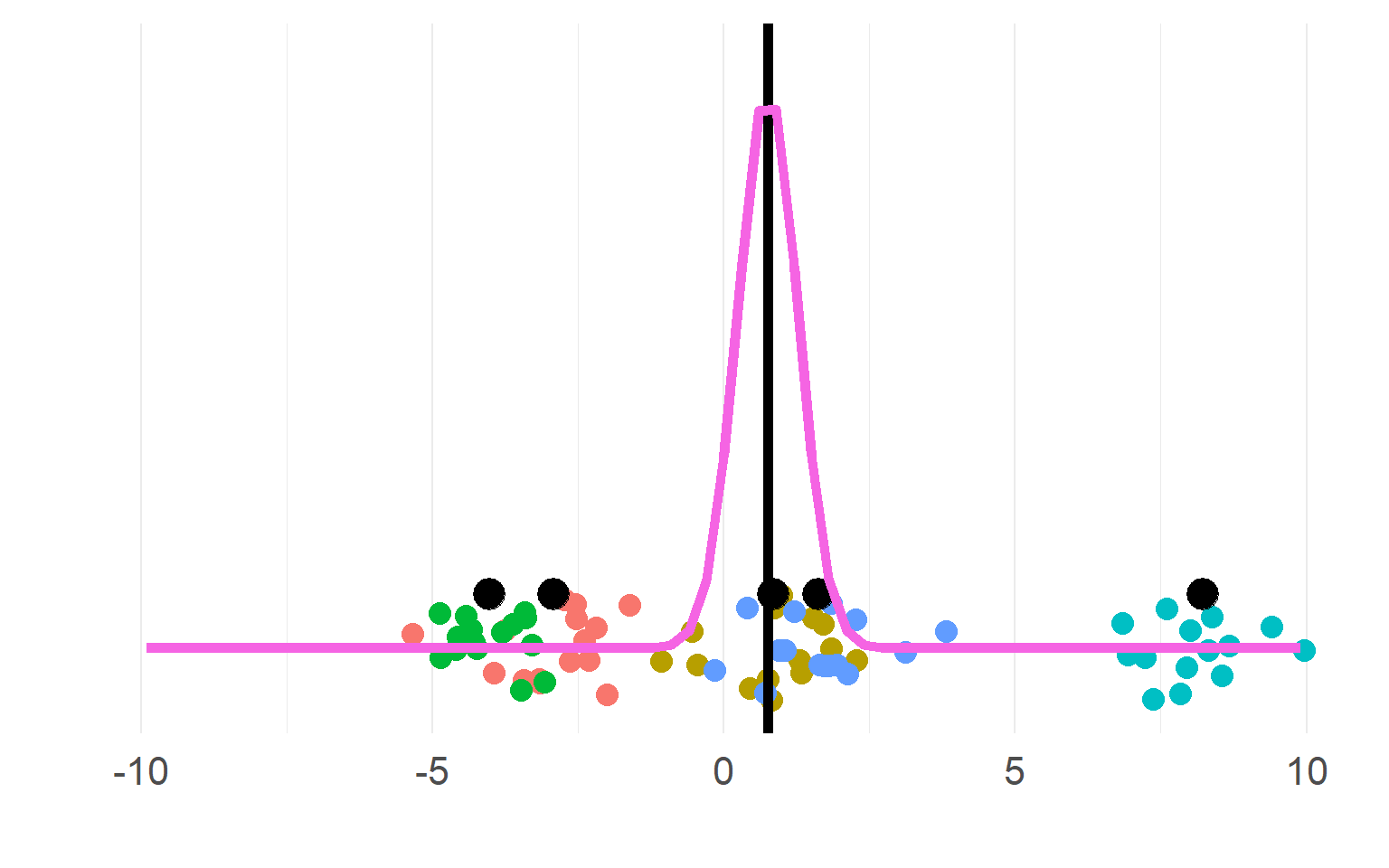
Sampling distributions
 (pink for aggregate, purple for disaggregate). There is a strong allure to choose the purple one, easier to get significant results!
(pink for aggregate, purple for disaggregate). There is a strong allure to choose the purple one, easier to get significant results!
\[n_{subject}(aggregate) = df+1 = 5\] \[n_{"subject"}(pseudoreplication) = df+1= 5*5 = 25\]
DONT DO THIS, YOU KNOW (now) BETTER
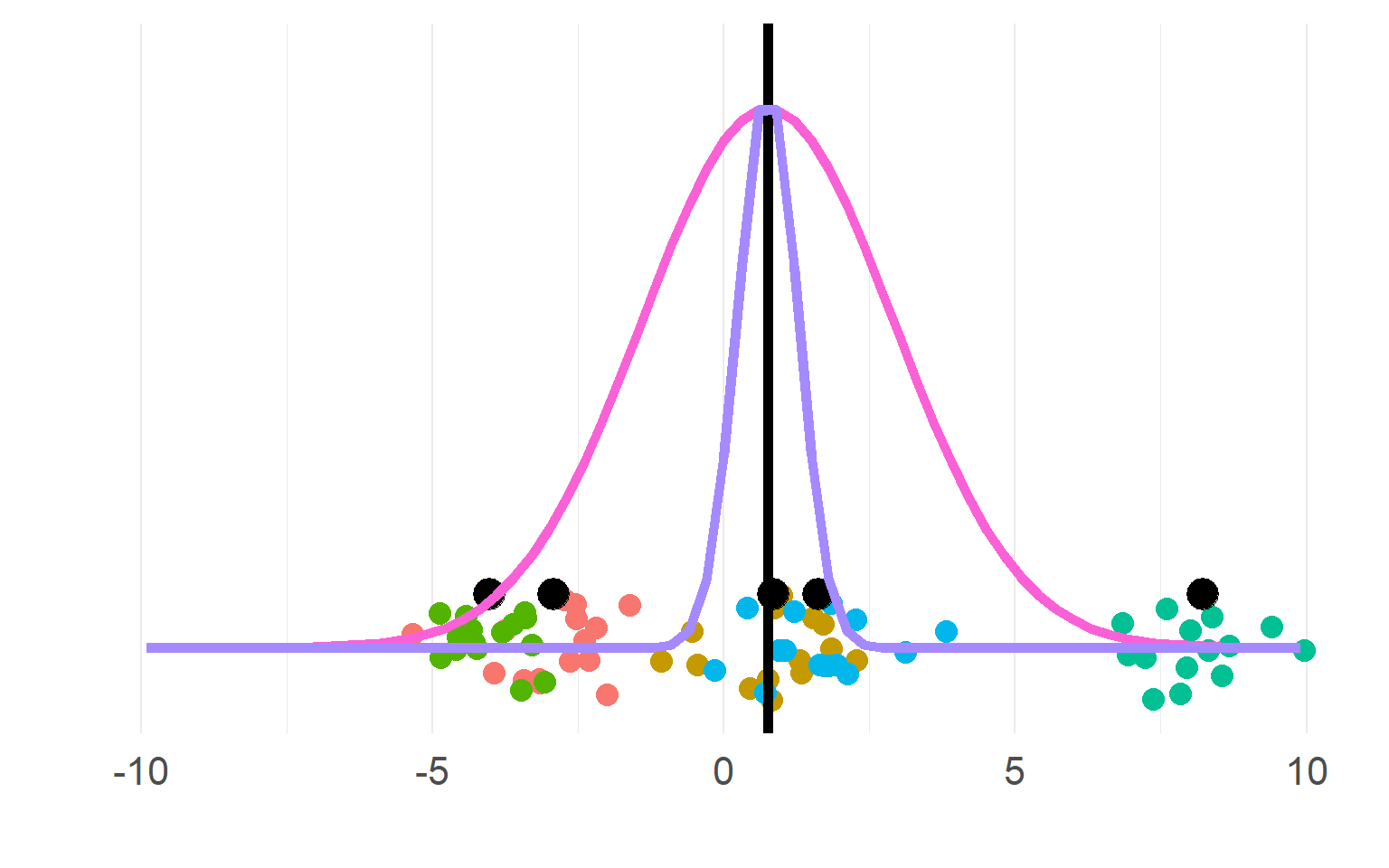
Always necessary to aggregate?
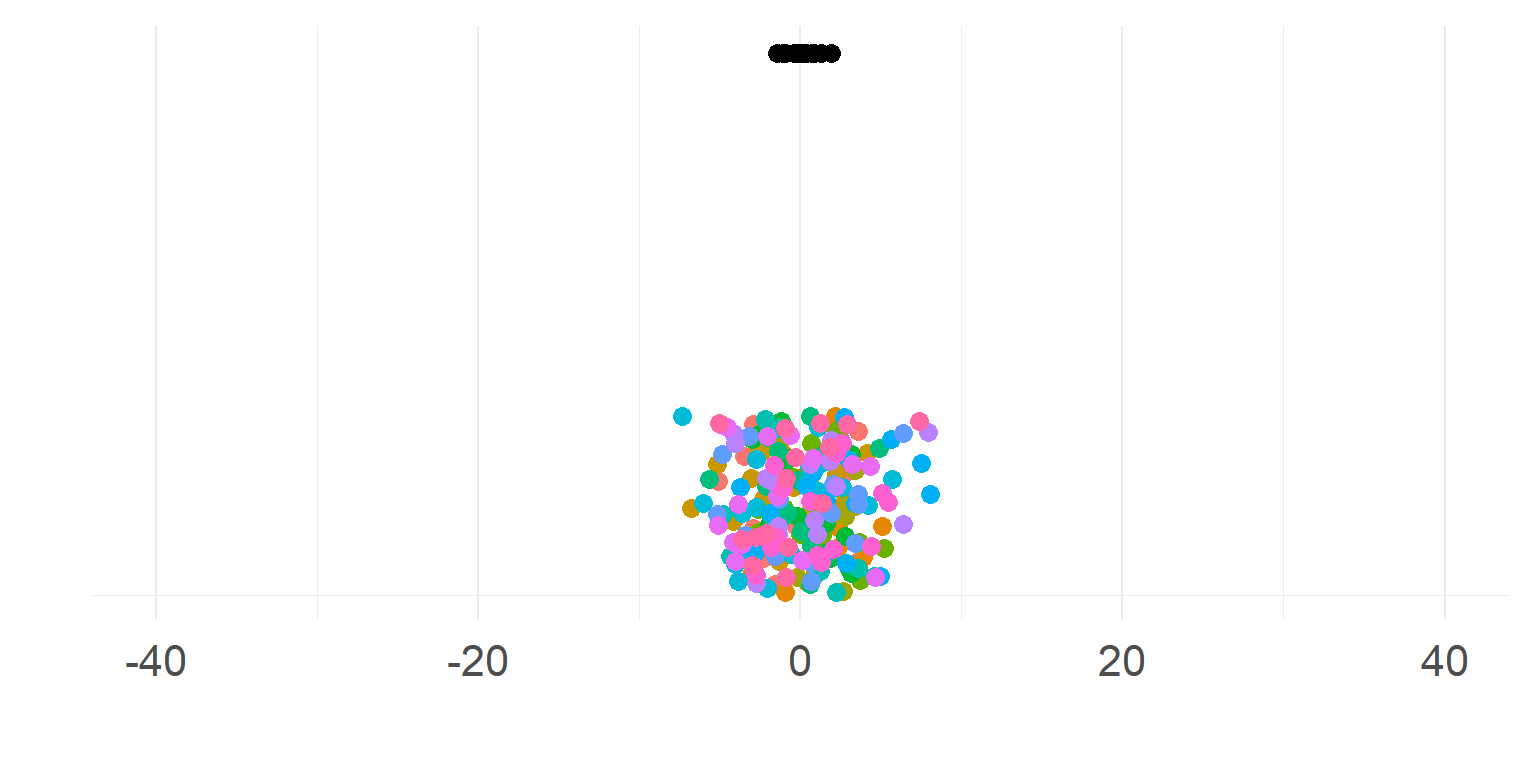 \[\sigma_{within} >> \sigma_{between}\]
\[\sigma_{within} >> \sigma_{between}\]
Subjects are very similar
Not so necessary to aggregate first
A single parameter summarizes subject-means well
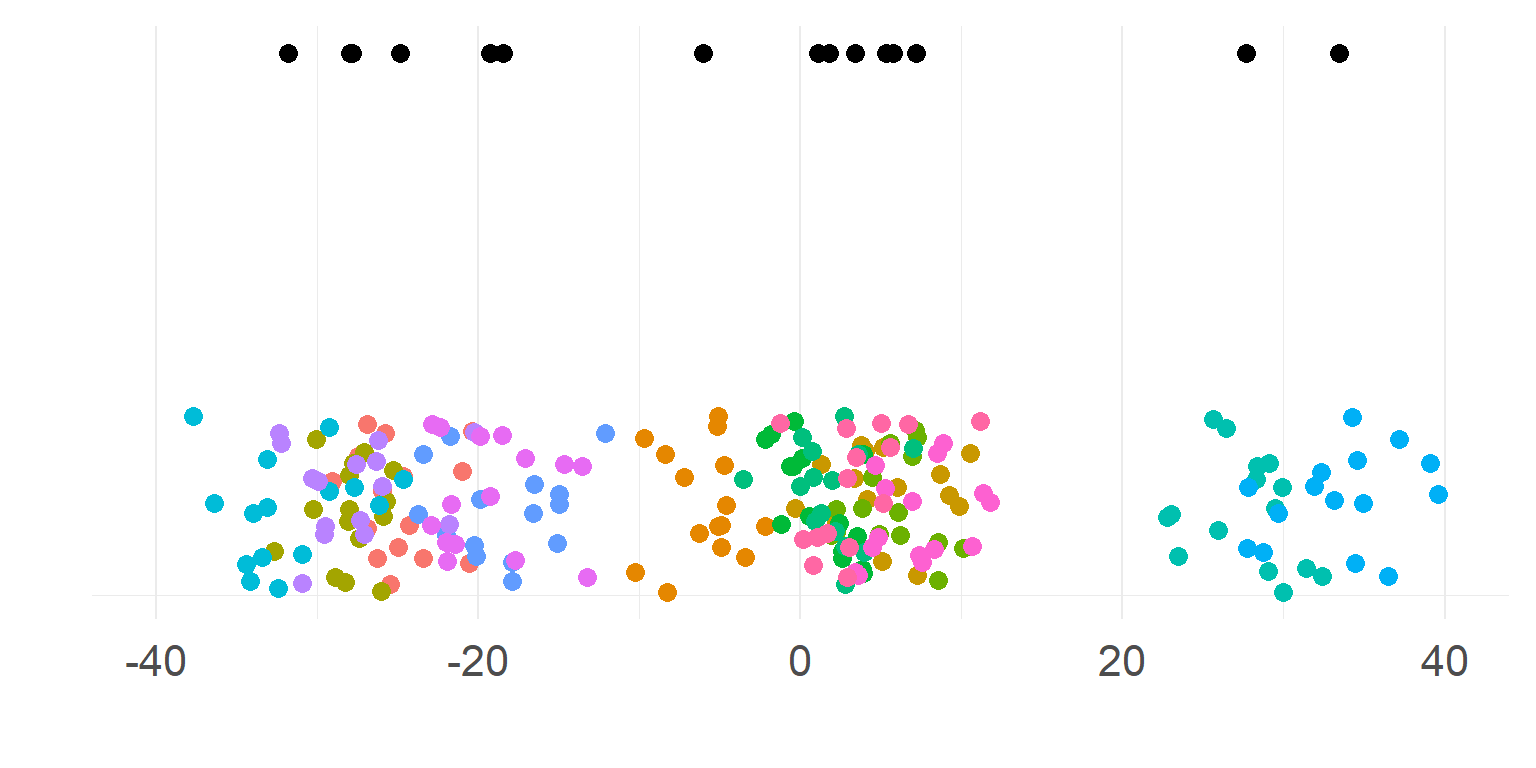 \[\sigma_{within} << \sigma_{between}\]
\[\sigma_{within} << \sigma_{between}\]
Subjects are very different
Totally necessary to aggregate first
\(n_{subject}\) parameters summarizes subject-means well
’
Should we trust all subjects equally?
Question: Estimate the mean of the population
Should we trust all subjects equally?
Question: Estimate the mean of the population
Should we trust all subjects equally?
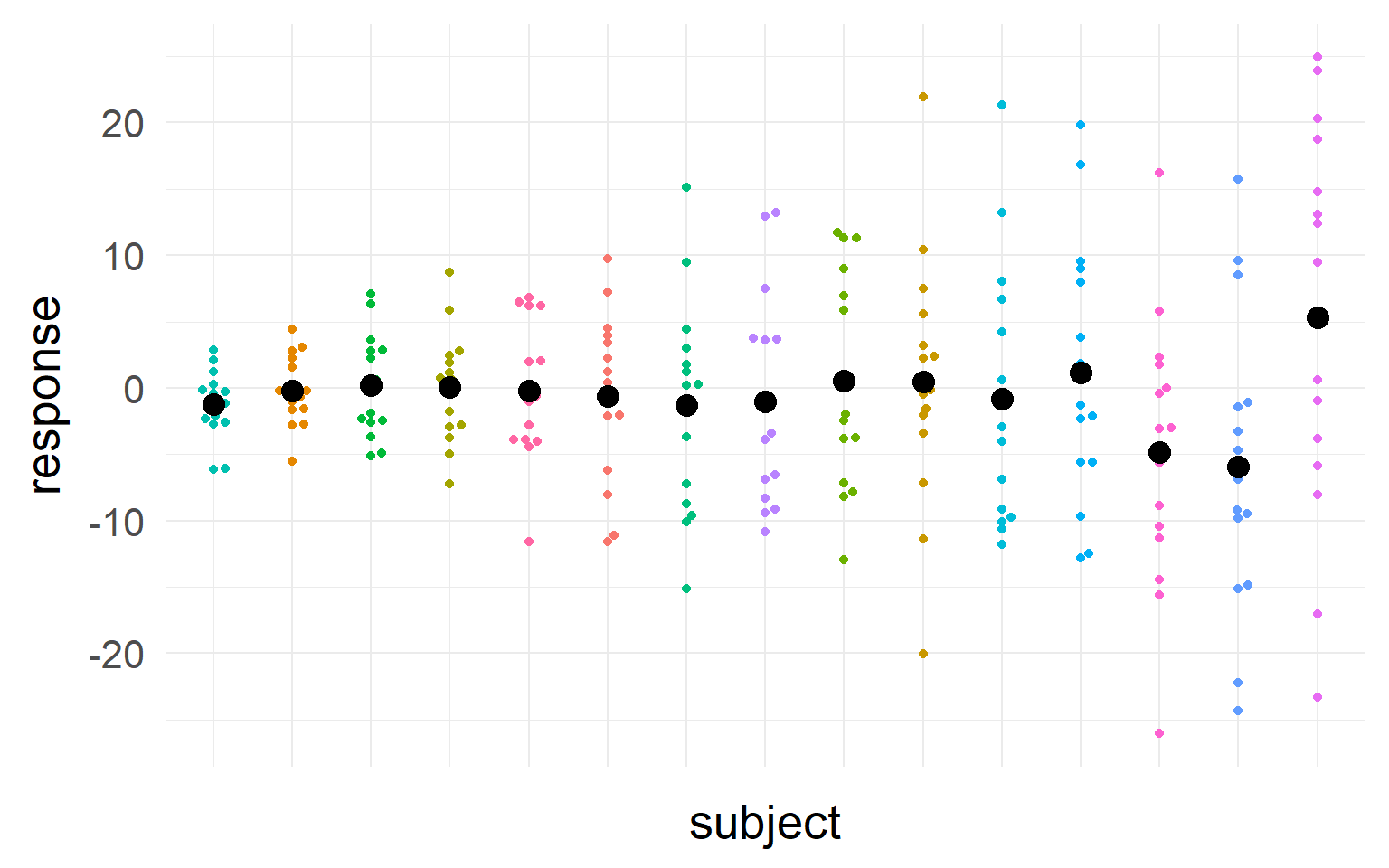
We should take into account sample-size and variance into our estimate of the population mean
We should trust those subjects more, where we most sure about their central tendency
Summary
- Why repeated measures
- More power to find effects that exist!
- Don’t forget about repeated measures!
- Else your type I error will be very high
- Should we trust all subjects equally?
- No, we should punish for small within-subject sample-size and punish high variance
Overview
- Repeated measures
- An example to guide you through the steps
- The mixed model
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
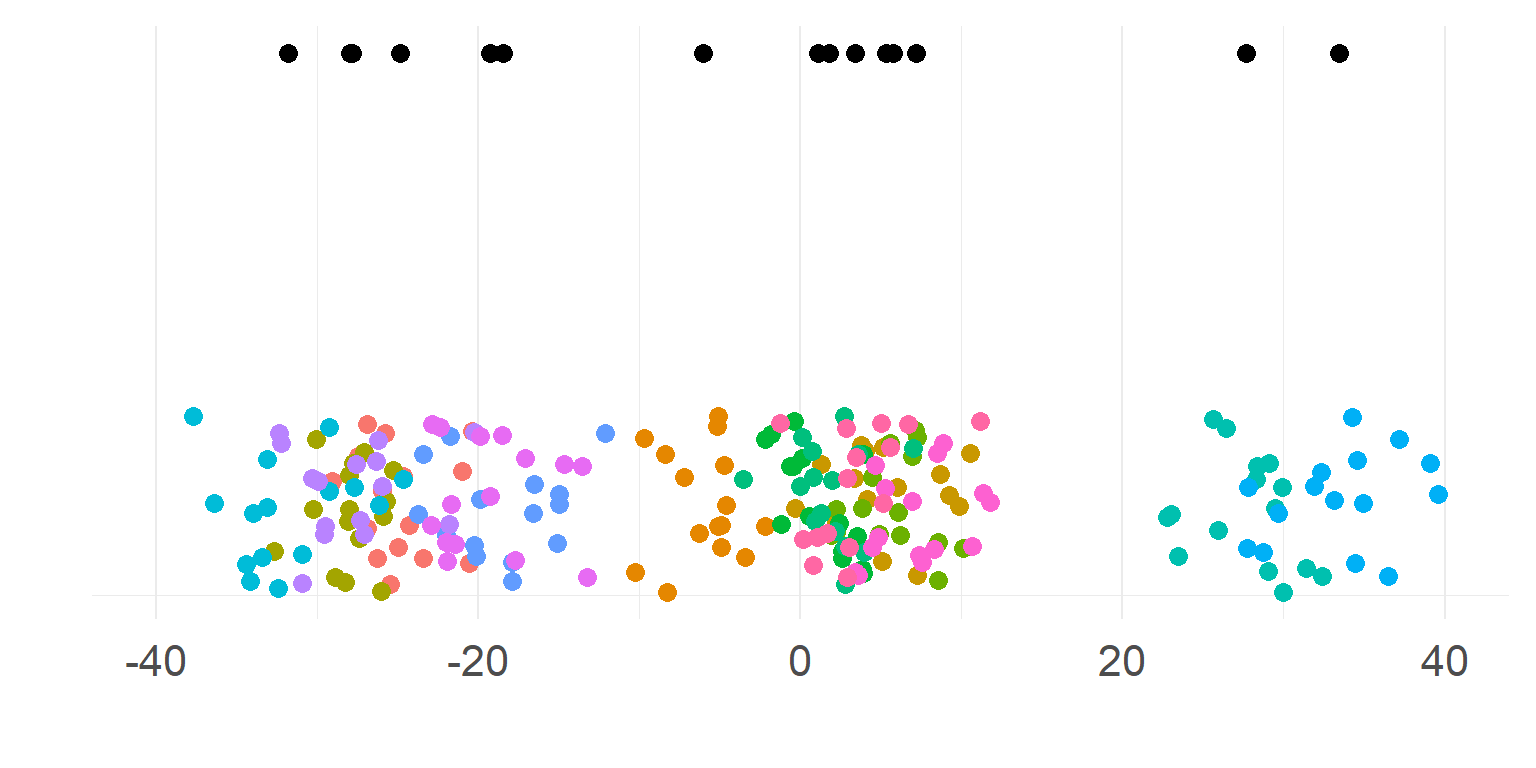
The example

EEG-Experiment: Contrast vs. P100 size
=> Very noisy subjects (babys?), between 4 and 29 trialsThe data
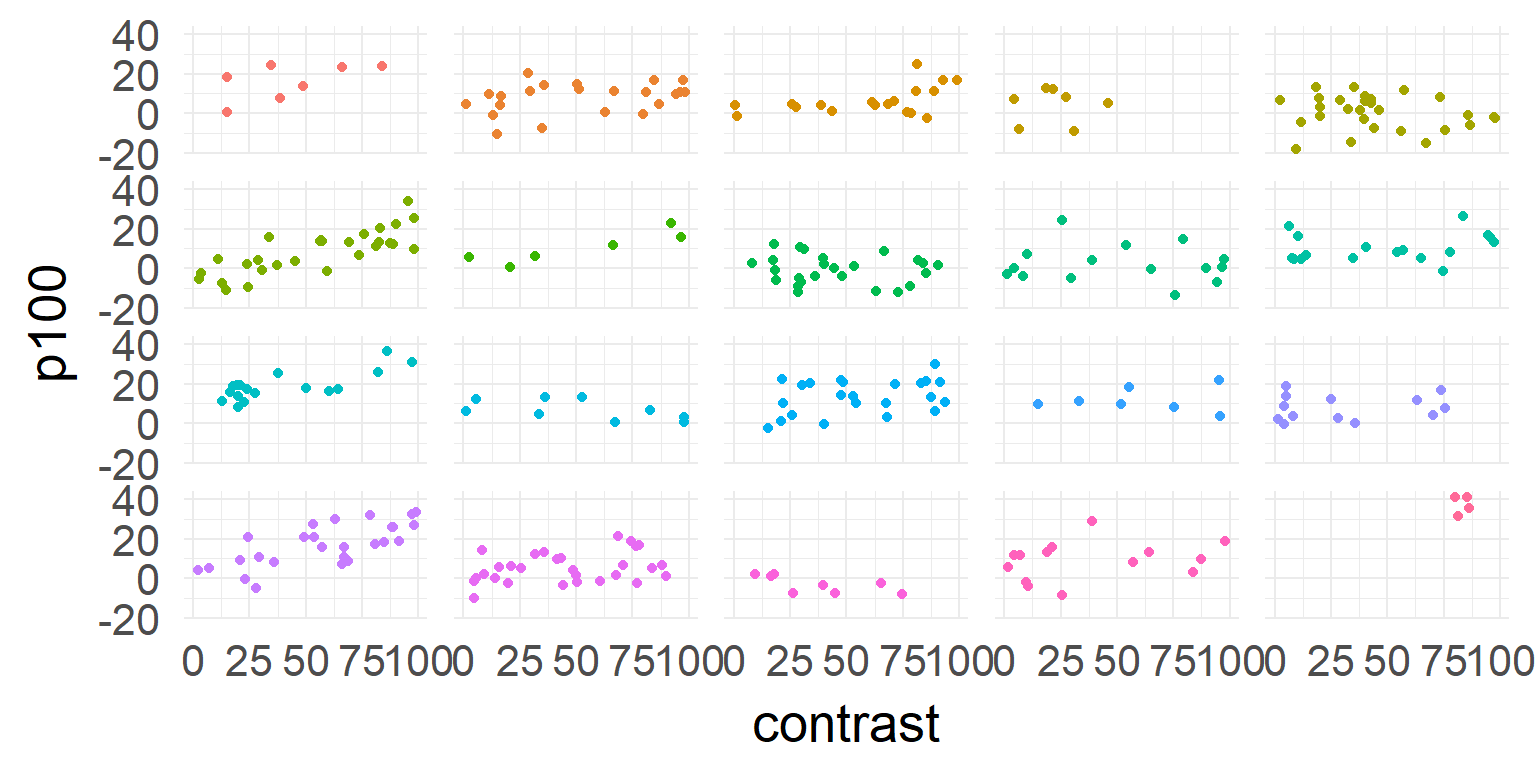
one model for all subjects
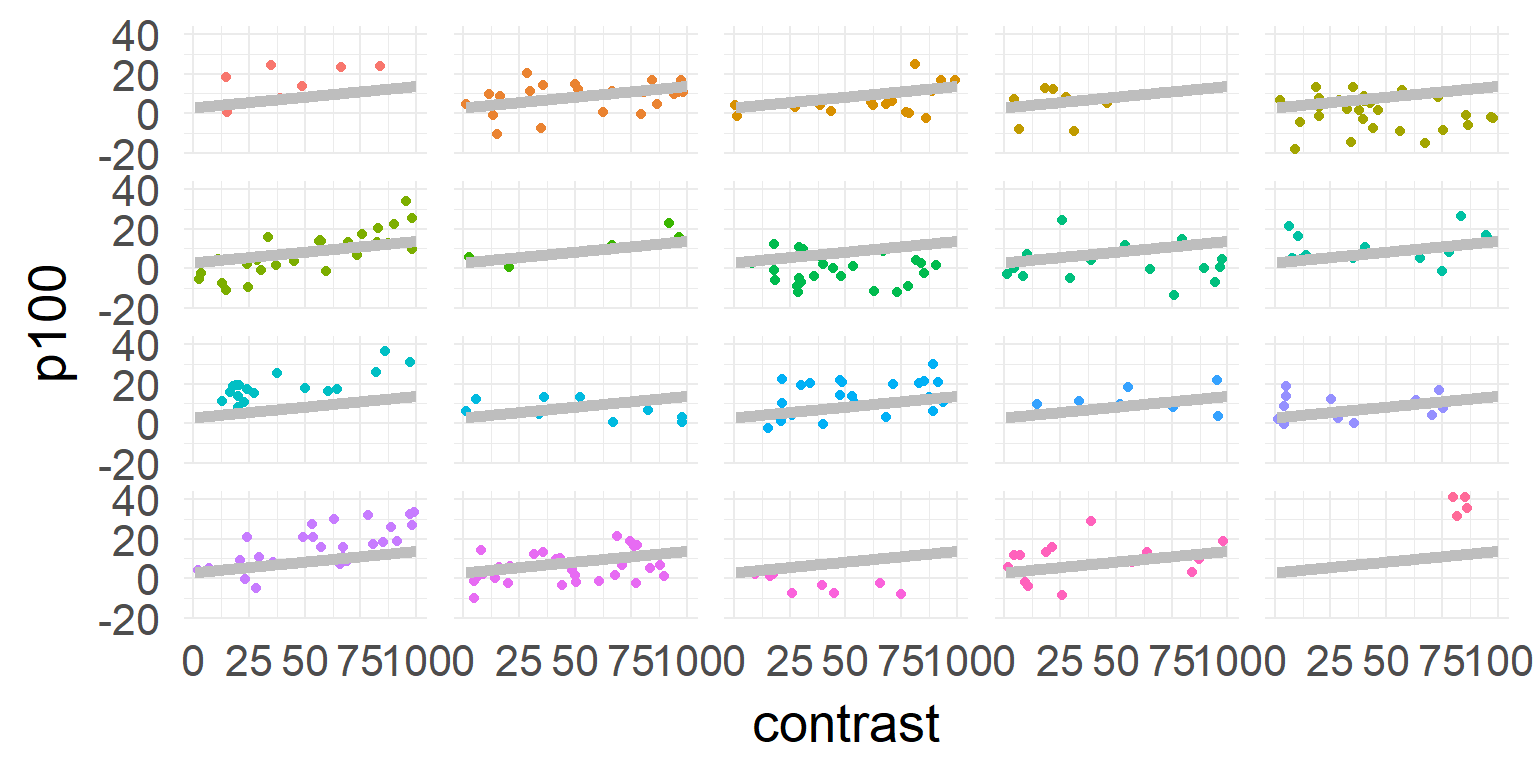 \[\hat{y} = \beta_0 + \beta_1 * contrast \]
\[\hat{y} = \beta_0 + \beta_1 * contrast \]
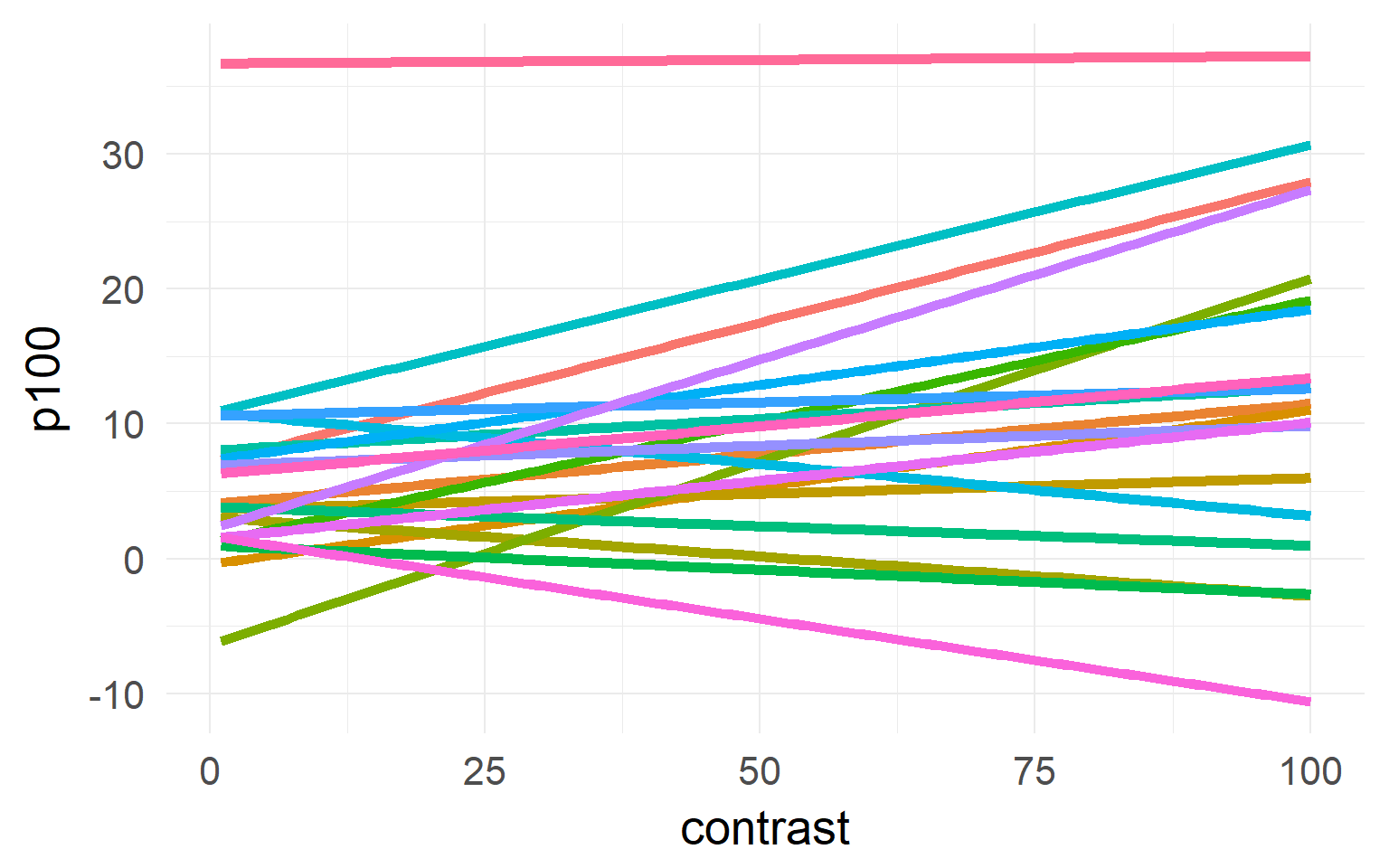
one model for each subject
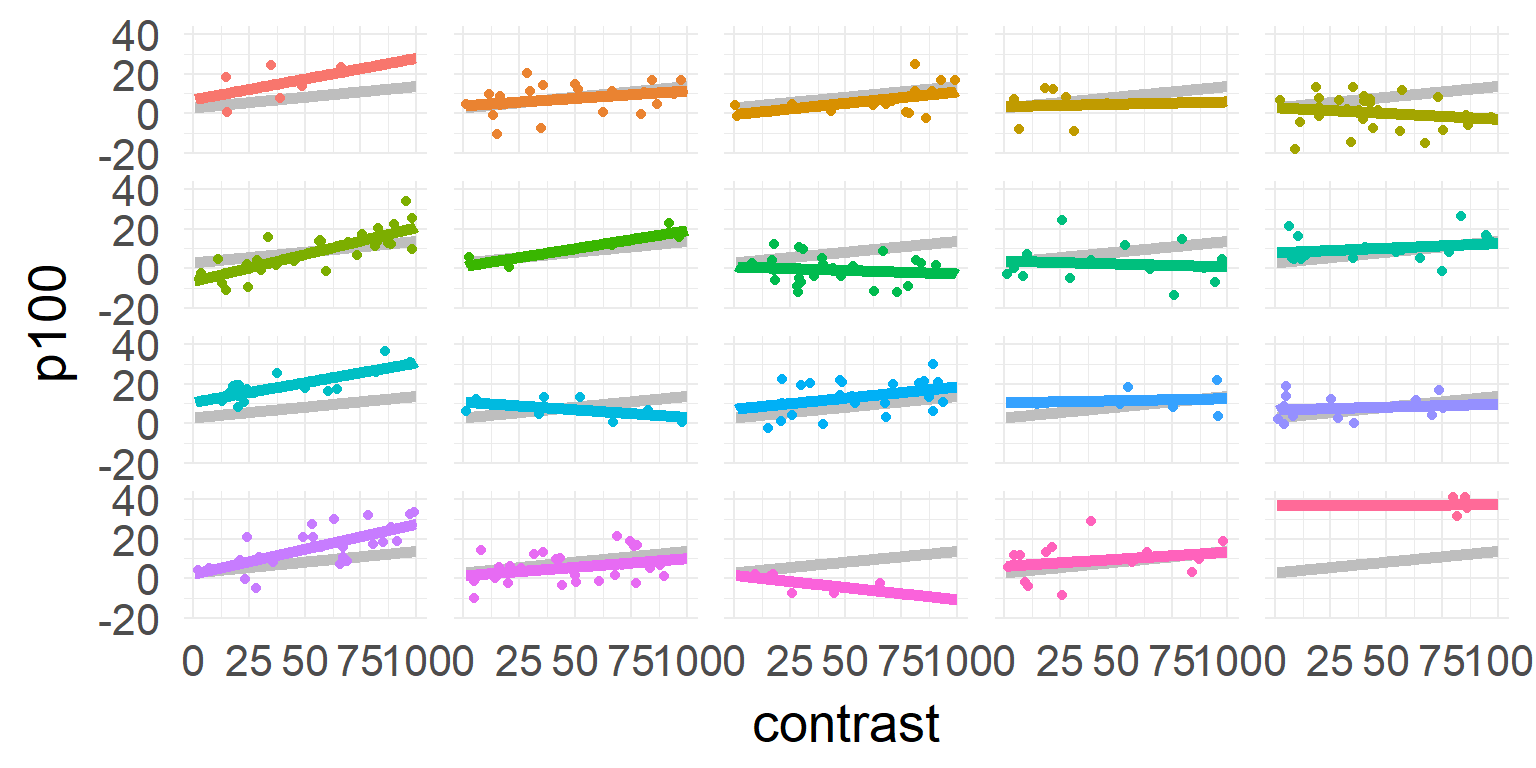 \[\hat{y_j} = \beta_{0,j} + \beta_{1,j} * contrast \]
\[\hat{y_j} = \beta_{0,j} + \beta_{1,j} * contrast \]
Excourse: two-stage statistics
One solution
Linear Mixed Model aka Hierarchical Model aka Multilevel Model
A compromise
Small second level variance (limit \(0\))
Parameters/DF assumed to be n-trials
Large second level variance (limit \(\infty\))
Parameters/DF assumed to be subjects
Overview
- Repeated measures
- An example to guide you through the steps
- The mixed model
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
Formal definition of the linear mixed model
A word of warning
Encouraging psycholinguists to use linear mixed-effects models ‘was like giving shotguns to toddlers’ (Barr)
Because mixed models are more complex and more flexible than the general linear model, the potential for confusion and errors is higher (Hamer)
Many ongoing riddles:
Book:Richly Parameterized Linear Models
- Chp. 9: Puzzles from Analyzing Real Data sets
- Chp.10: A Random Effect Competing with a Fixed Effect
- Chp.12: Competition between Random Effects
- Chp.14: Mysterious, Inconvenient or Wrong Results from Real Datasets
The mixed model in R
\(\hat{y} = \beta_0 + \beta_1 * contrast + u_{0,j} + u_{1,j} * contrast\)
\(\hat{y}_j = \beta X_j + b_jZ\)
Fitting this in R using the package lme4
response ~ beta + (beta|group)
In our example:
response ~ 1 + contrast + (1|subject) + (0+contrast|subject)
Mixed models in R
summary(lmer(p100~1 + contrast + (1 + contrast||subject),data=d))## Linear mixed model fit by REML ['lmerMod']
## Formula: p100 ~ 1 + contrast + ((1 | subject) + (0 + contrast | subject))
## Data: d
##
## REML criterion at convergence: 2271.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.71978 -0.62658 -0.01064 0.65739 2.91110
##
## Random effects:
## Groups Name Variance Std.Dev.
## subject (Intercept) 10.16741 3.1886
## subject.1 contrast 0.01353 0.1163
## Residual 54.45510 7.3794
## Number of obs: 323, groups: subject, 20
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 4.03422 1.10536 3.650
## contrast 0.09536 0.03045 3.131
##
## Correlation of Fixed Effects:
## (Intr)
## contrast -0.324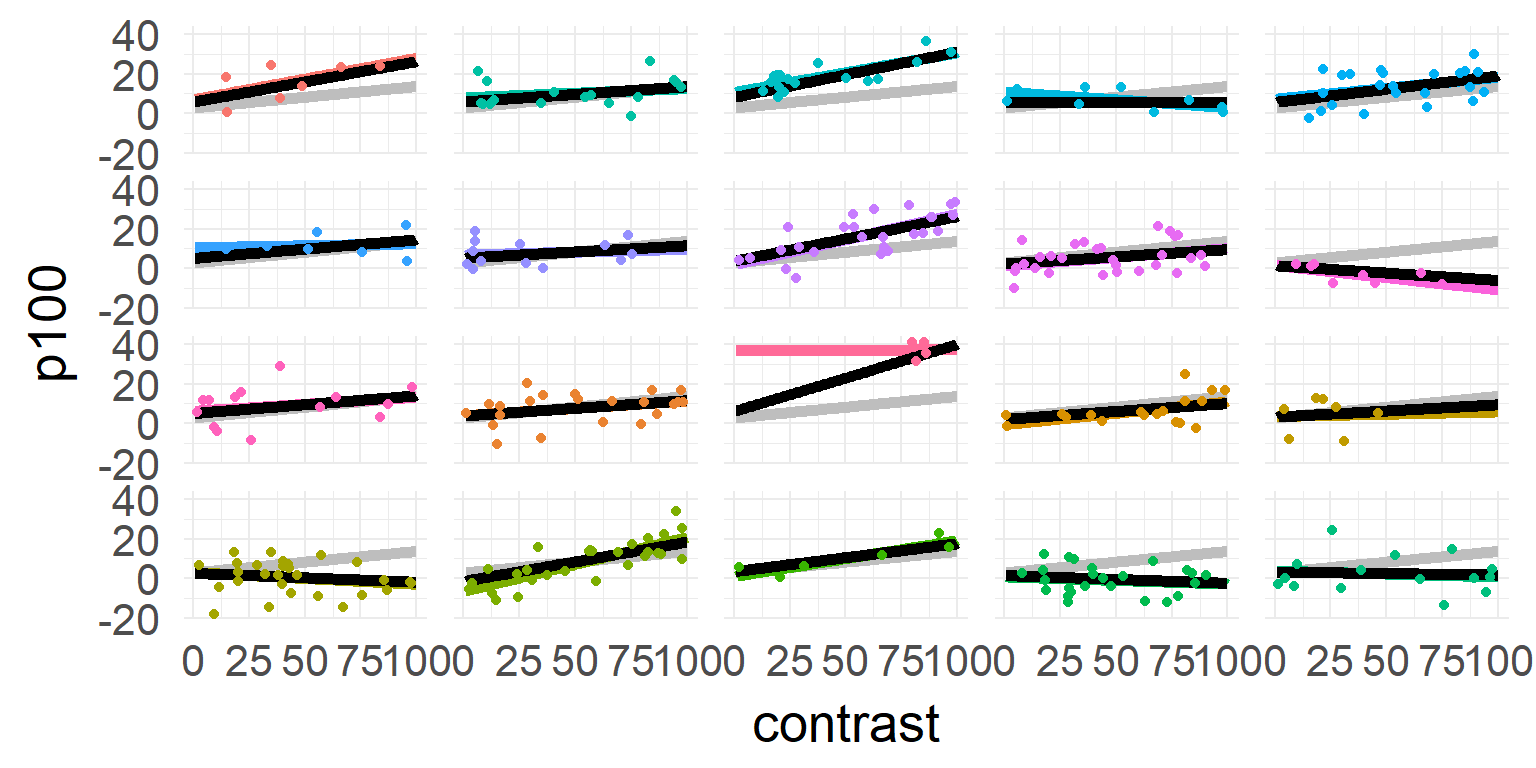
Overview
- Repeated measures
- An example to guide you through the steps
- The mixed model
- Inference
- REML vs ML
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
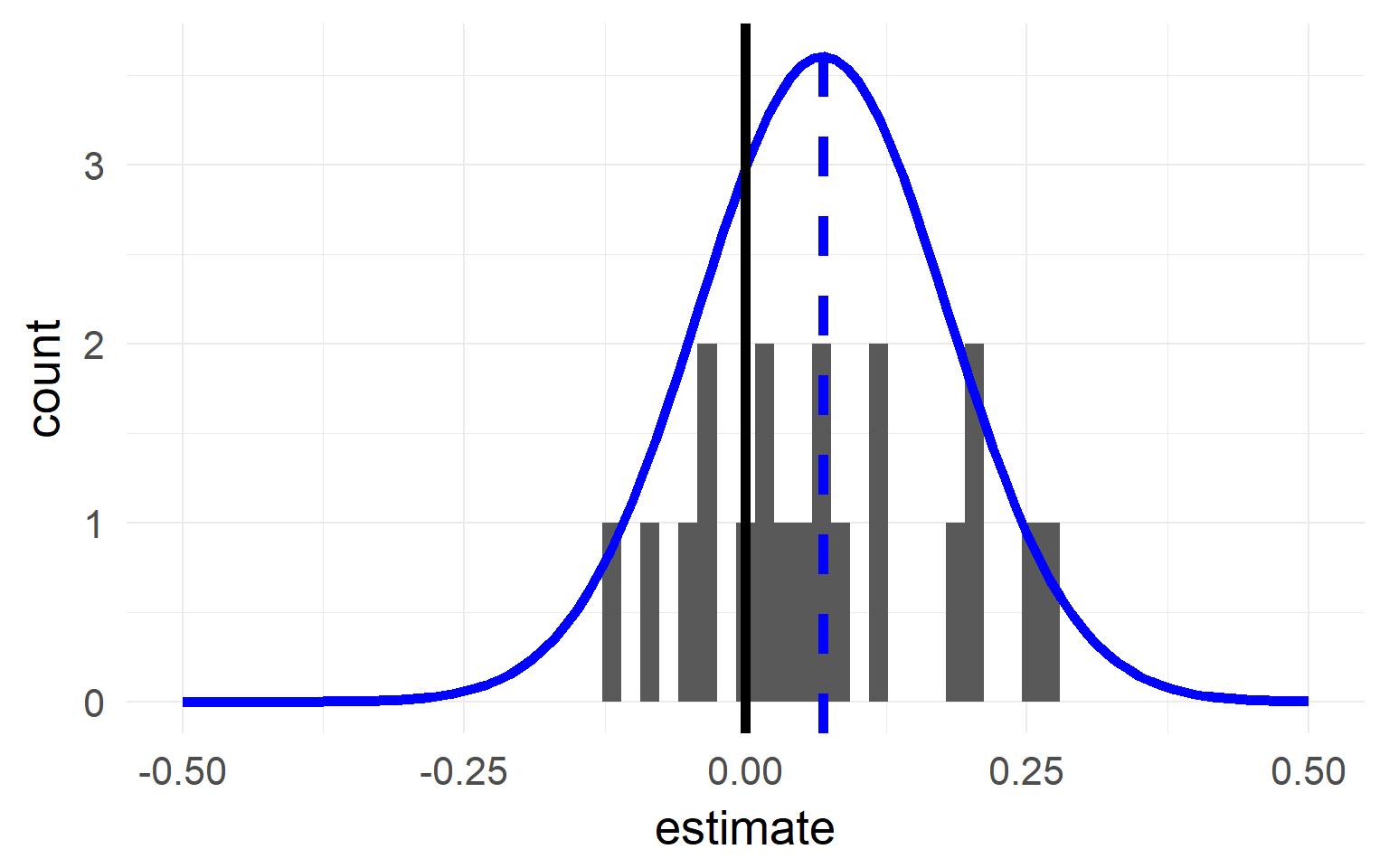
Model-Comparisons aka p-values
Unresolved problem!
Read (three links):how to get p values, problems with stepwise regression, different ways to get p-values
One way (good and common, but not the best*): Model comparison for fixed effects:
Be sure to keep random structure equal
anova(mres0,mres1)“refitting model(s) with ML (instead of REML)”
## Data: d
## Models:
## mres0: p100 ~ 1 + (1 + contrast | subject)
## mres1: p100 ~ 1 + contrast + (1 + contrast | subject)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## mres0 5 2286.5 2305.3 -1138.2 2276.5
## mres1 6 2280.1 2302.7 -1134.0 2268.1 8.4095 1 0.003733 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1* currently bootstrapping or mcmc recommended
REML VS ML
Intuition:
When estimating the variance parameter using maximum likelihood (ML) \(\sigma\) is biased because \(\mu\) is not known at the same time
Solution:
Fit all fixed effects \(\mu\), then refit the variance parameters on the residing estimates.
This is called restricted maximum likelihood (REML). If \(n\) is large, no difference between ML and REML exist. If \(n\) is small REML gives better predictive results.
If you do model comparison and fixed effects (should) differ (usual case) you have to use ML
Bootstrapping
- resample from the data with replacement (or parametrically from \(H_0\)-Model) 1000 times
- calculate statistic of interest
- observe spread of statistic
b1 <- bootMer(mres1, FUN = function(x) as.numeric(logLik(x)), nsim = nboot,seed = 1)
b2 <- bootMer(mres0, FUN = function(x) as.numeric(logLik(x)), nsim = nboot,seed = 1)
bootLL = 2 * b1$t - 2 * b2$t # grab the values & plot
quantile(bootLL, probs = c(0.025, 0.975))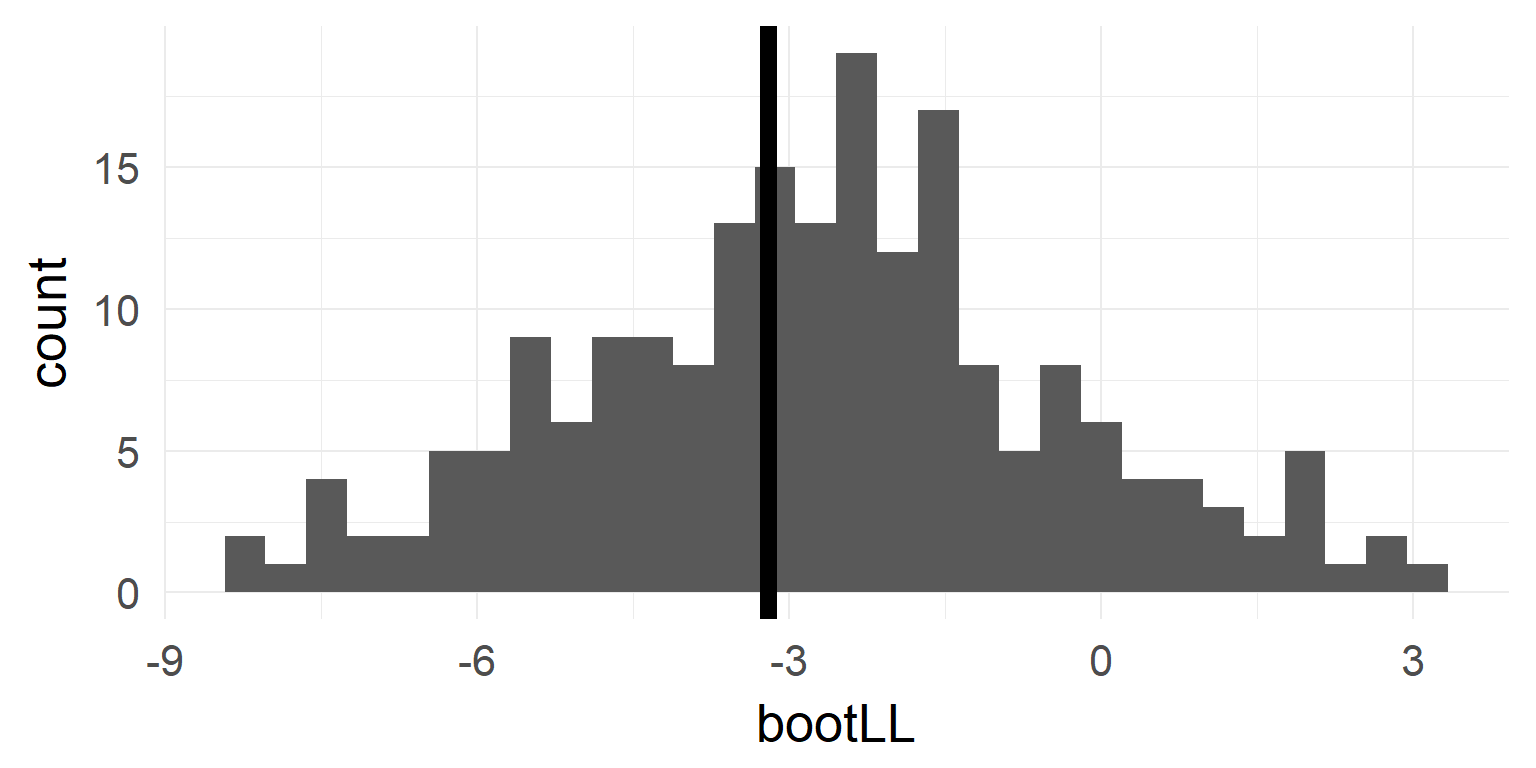
pbkrtest
Better & easier: Likelihood-Ratio using R-Package pbkrtest
summary(pbkrtest::PBmodcomp(mres1,mres0,nsim=nboot))## Parametric bootstrap test; time: 30.27 sec; samples: 200 extremes: 3;
## large : p100 ~ 1 + contrast + (1 + contrast | subject)
## small : p100 ~ 1 + (1 + contrast | subject)
## stat df ddf p.value
## PBtest 8.3917 0.019900 *
## Gamma 8.3917 0.011404 *
## Bartlett 7.0365 1.0000 0.007986 **
## F 8.3917 1.0000 12.385 0.013029 *
## LRT 8.3917 1.0000 0.003769 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The main con against bootstrapping is the high computational time (use at least 1000 not 200 as in this example)
Overview
- Repeated measures
- An example to guide you through the steps
- The mixed model
- Inference
- Assumption checking
- Level 1
- Level 2
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
Checking Assumptions Level I
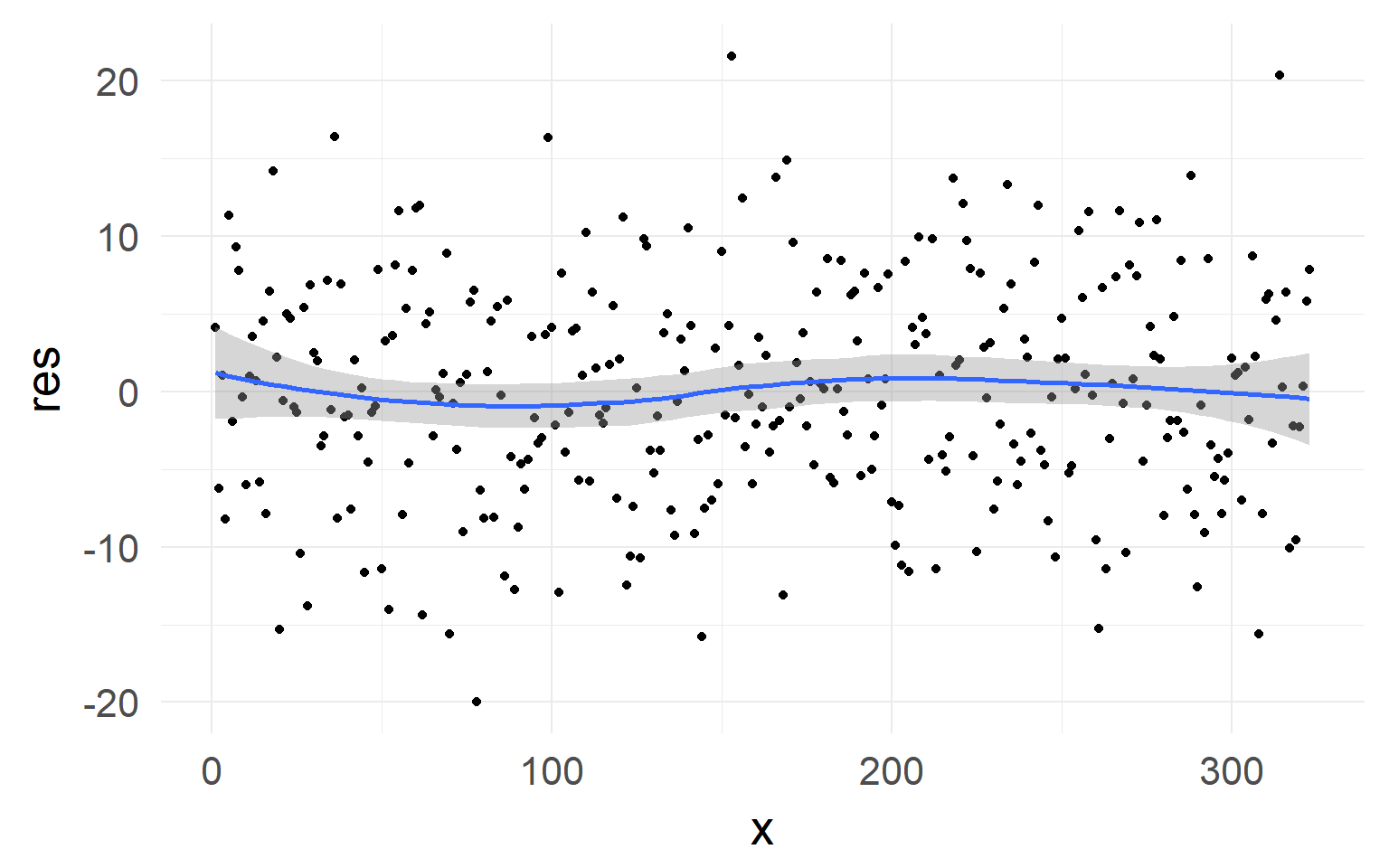
No strong non-linearity visible in residuals
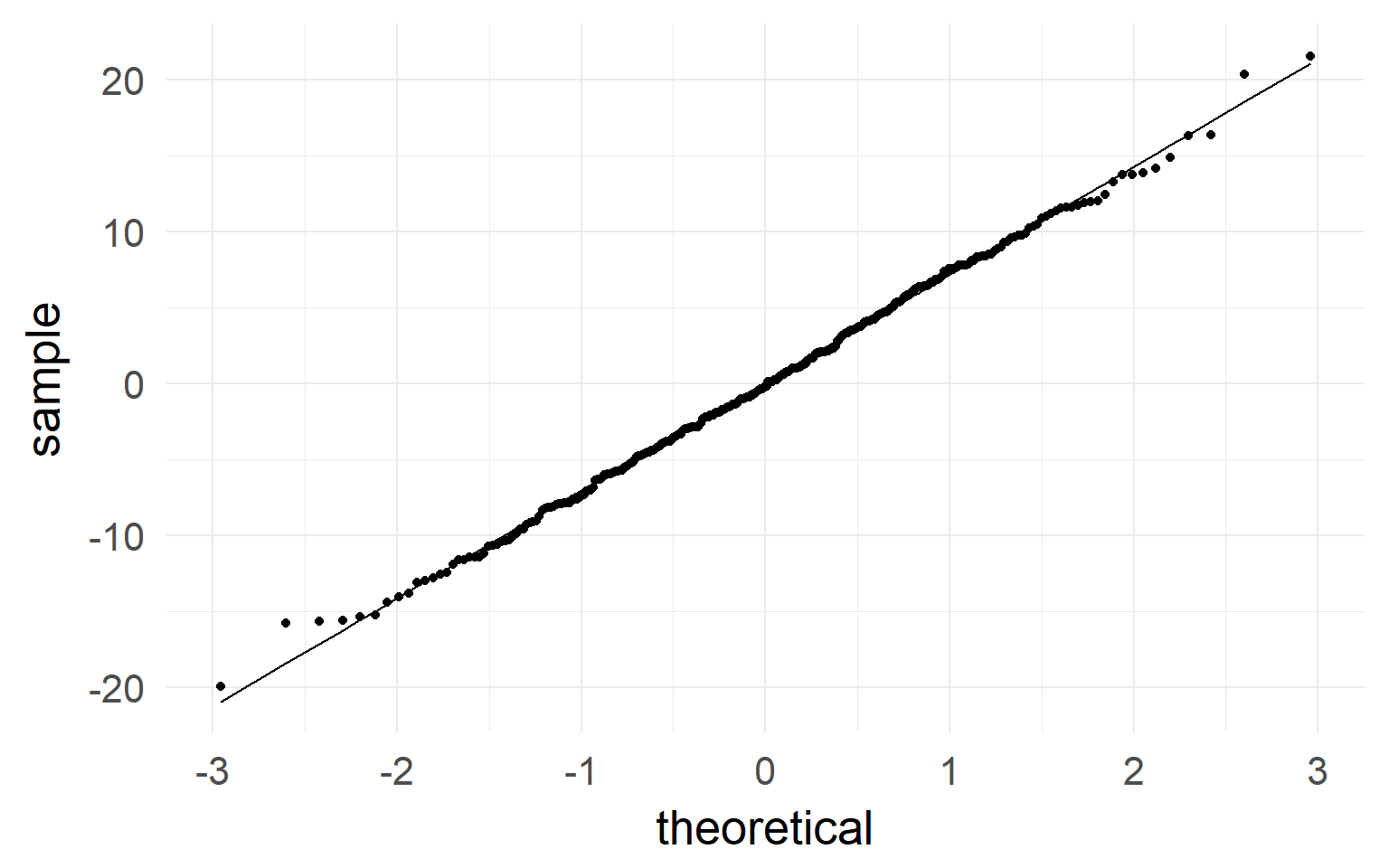
qqplot indicates normality of residuals
Checking assumptions Level II
In addition: test whether normality for random-variable is true: 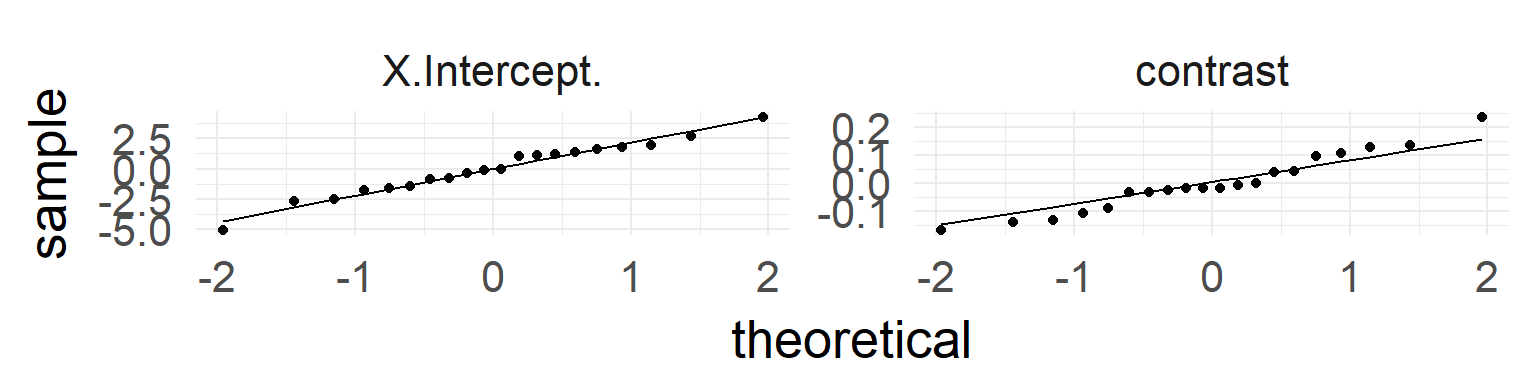
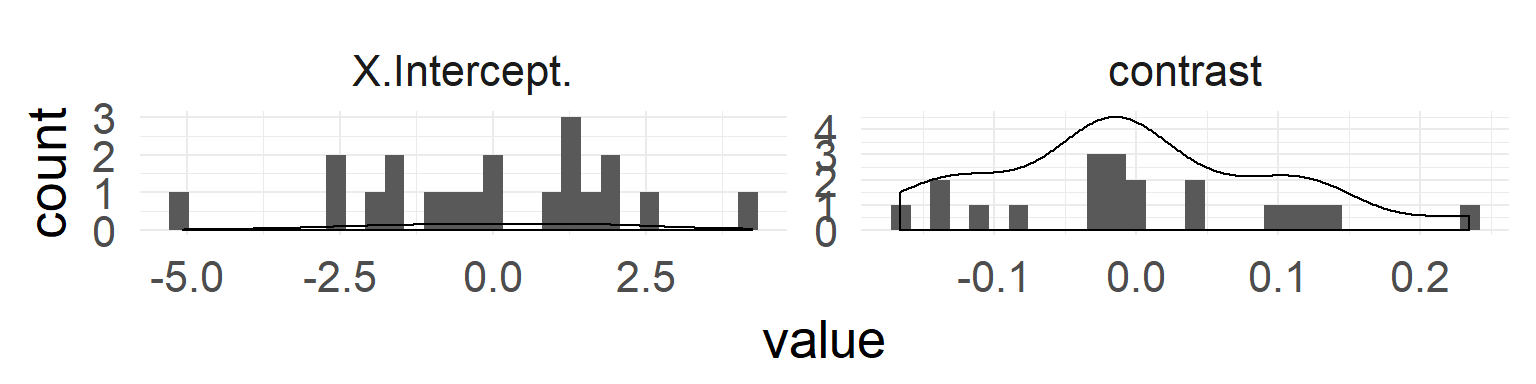
QQ-Plots indicate normality of both random effects.
Overview
- Repeated measures
- The mixed model
- An example to guide you through the steps
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
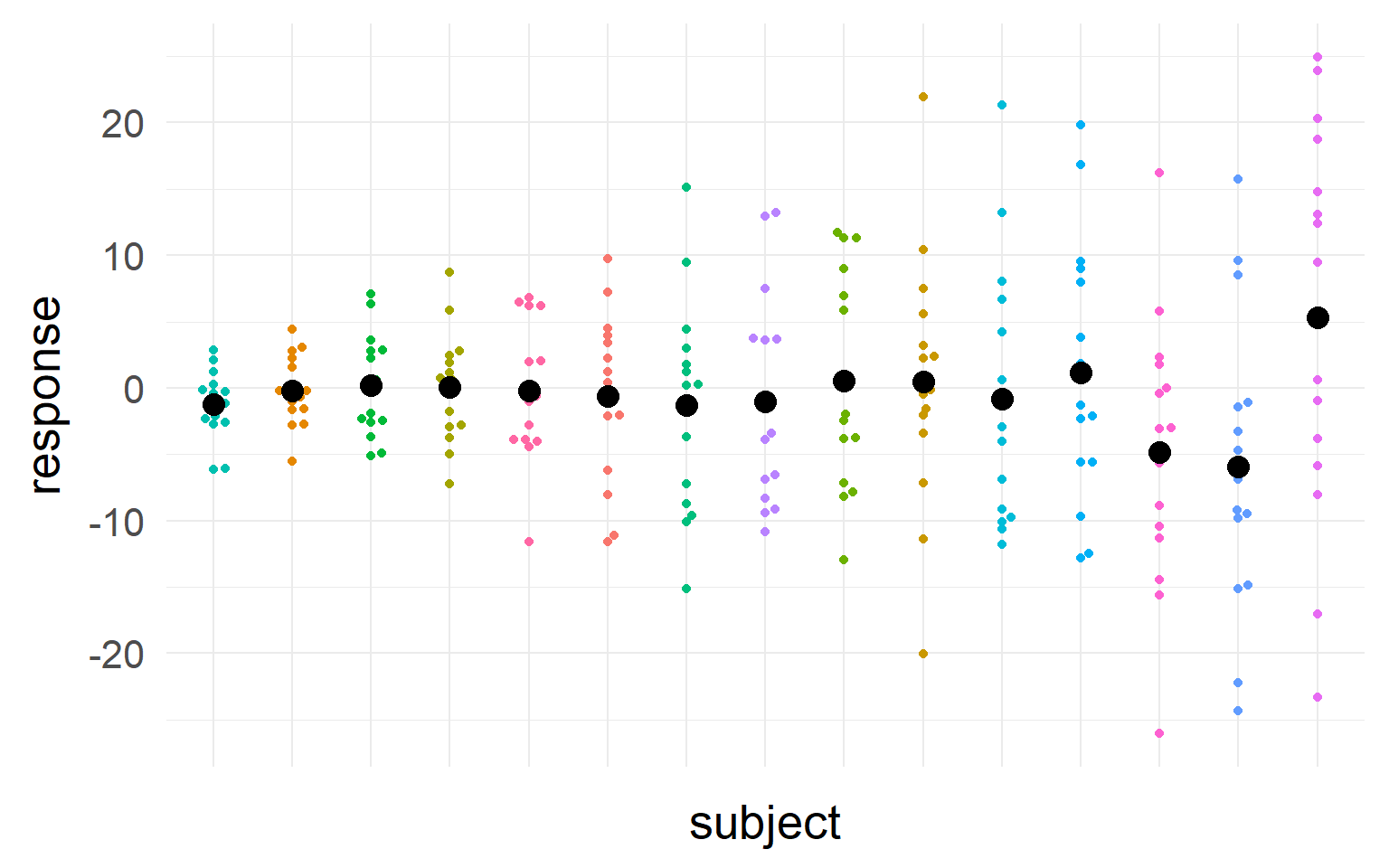
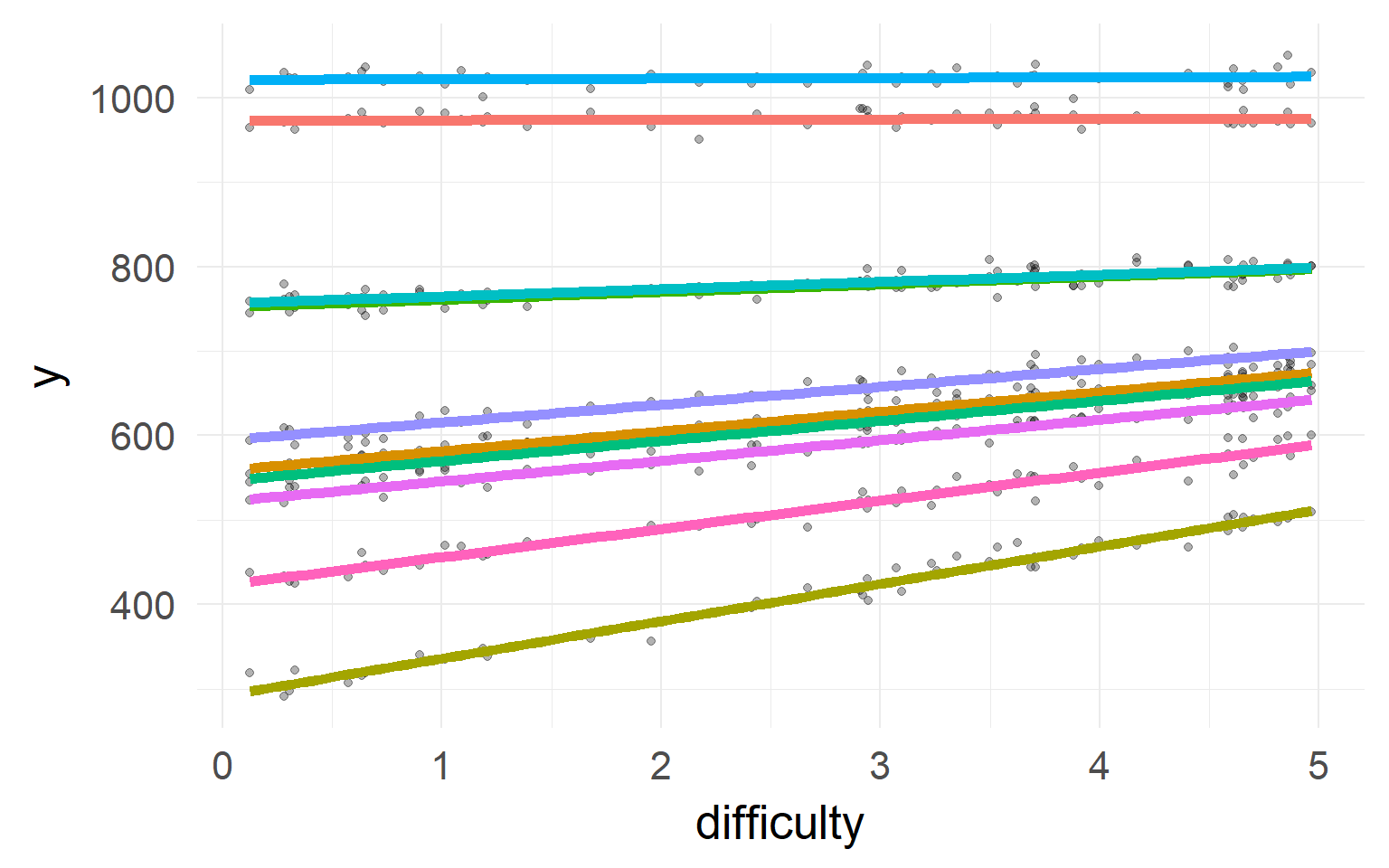
Shrinkage
The individual estimates with high variance / far off the population are shrinked inwards
Shrinkage-plot
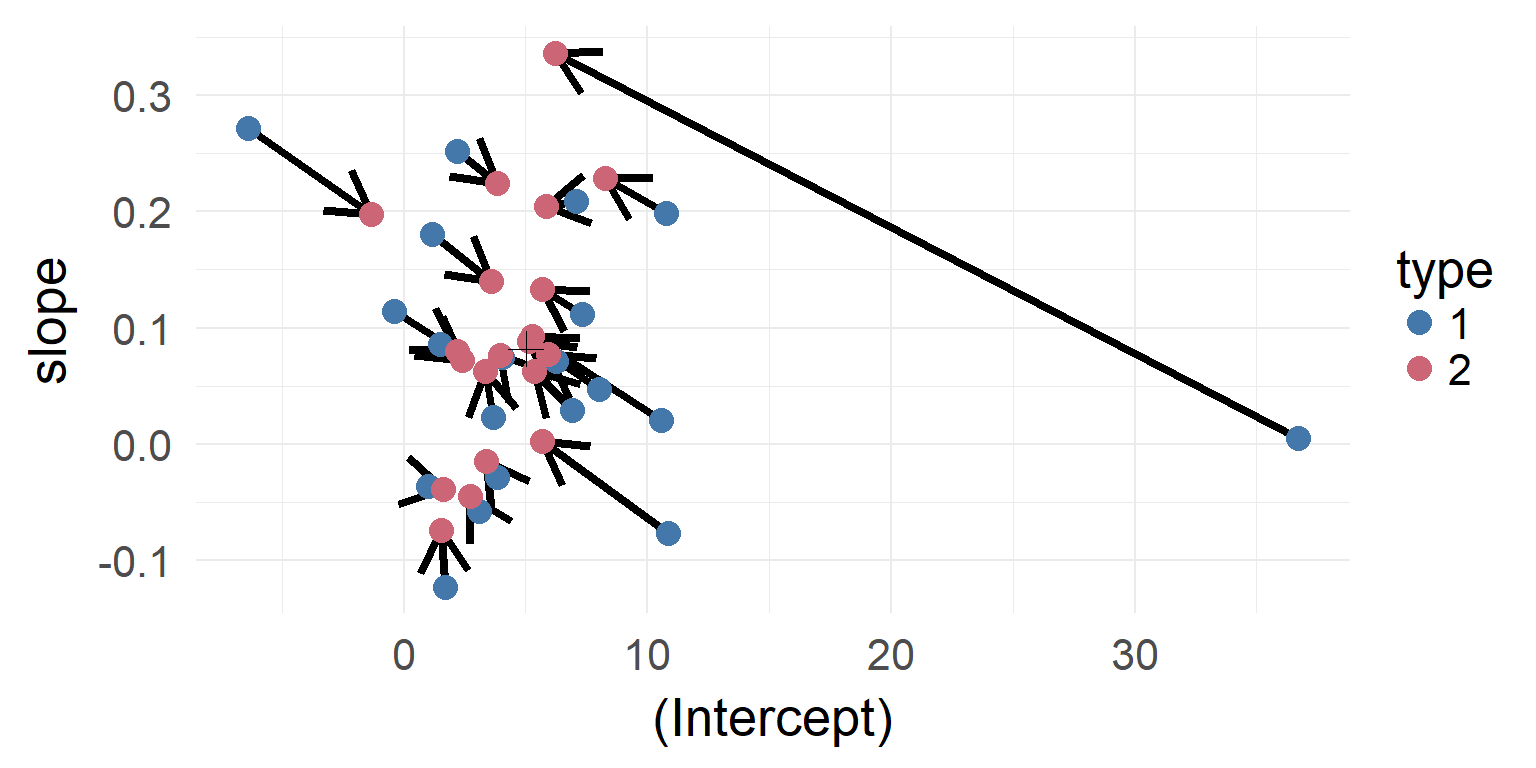
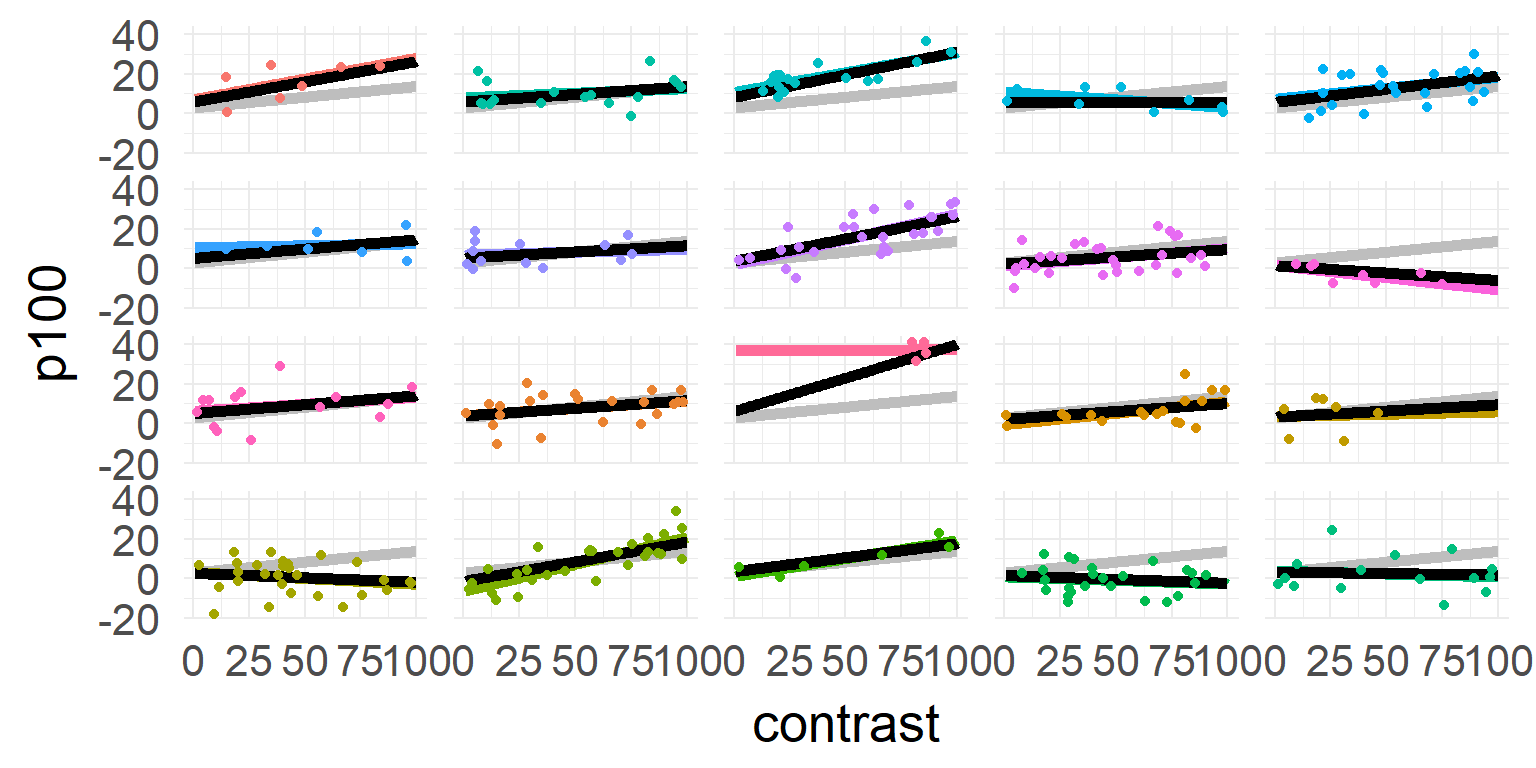
Shrinkage over multiple parameters
 Simulated data: Subjects with faster reaction time (intercept) show larger effects for difficulty (slope)
Simulated data: Subjects with faster reaction time (intercept) show larger effects for difficulty (slope)
In reverse: If I know somebody is generally slow, he should also have a smaller slope!
The multivariate normal I
The multivariate normal II
\(\rho = 0\), knowing one dimension does not tell you about the other
\[\sum = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0 &1 \end{array}} \right]\]
\(\rho = 0.6\), knowing one dimension tells you something about the other
\[\sum = \left[ {\begin{array}{*{20}{c}} 1&0.6 \\ 0.6 &1 \end{array}} \right]\]
Back to mixed models
\[\sum = \left[ {\begin{array}{*{20}{c}} 1&\rho \\ \rho &1 \end{array}} \right]\]
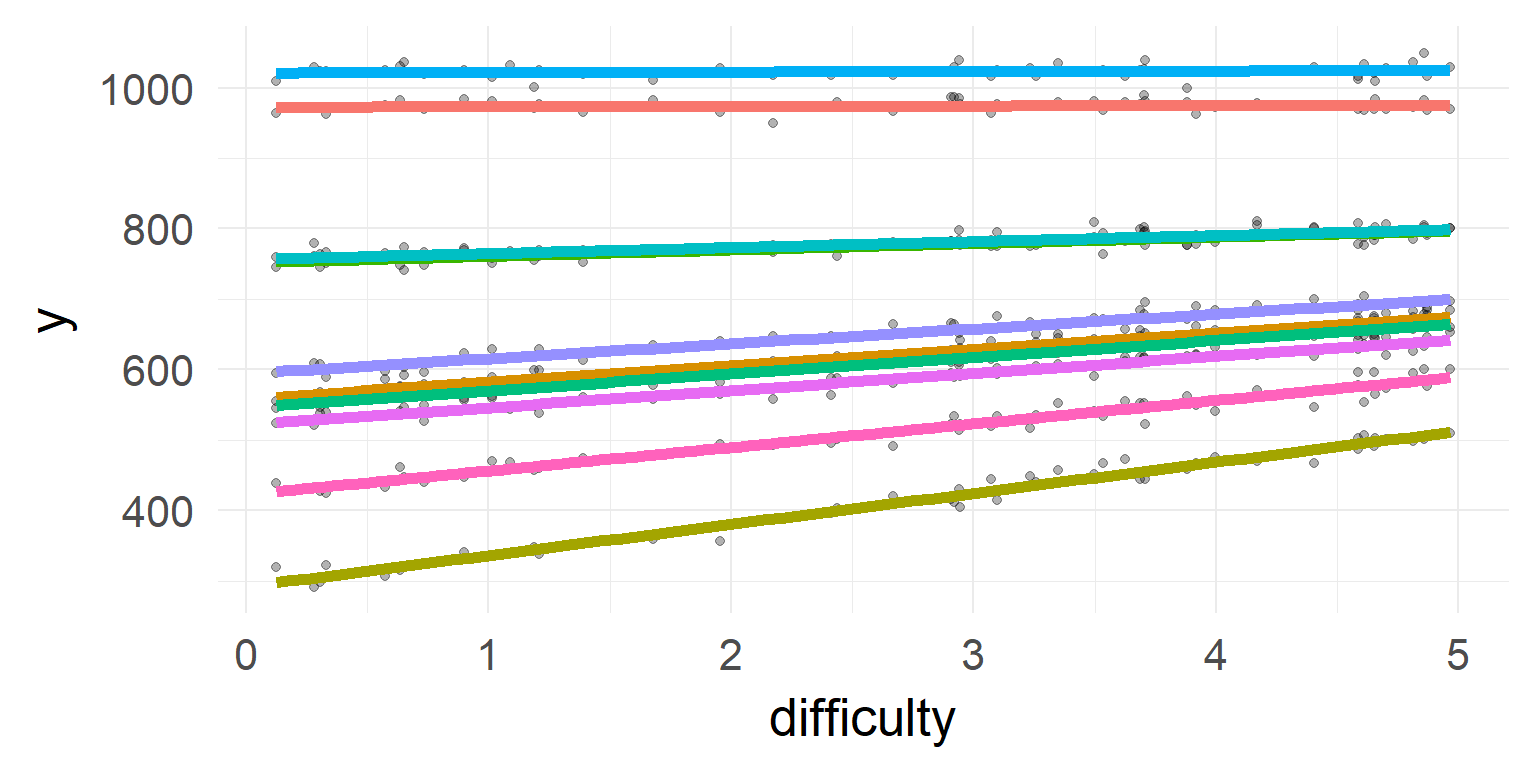
Overview
- Repeated measures
- The mixed model
- An example to guide you through the steps
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
Naming is a bit messy
Random/Fixed Coefficients
- Random intercept
- (1|subject): Different offset for each subject
- Random slope
- (predictor|subject): Different predictor-slope for each subject
- Random correlation
- (1+predictor|subject) or (X+Y|subject): Knowing about X tells you something about Y
- Fixed coefficient
- exactly the same for all subjects
Random/Fixed Variables
- Random variable
- Instance \(\in\) population, e.g. subjects, images, words
- Fixed variable
- limited number of possible values or no generalization to population needed, e.g. 3 different experimental conditions
Random effect also used for either random coefficient or random variable
Fixed effect usually refers to the estimator of the population mean
source and another 5 different definitions here
Overview
- Repeated measures
- The mixed model
- An example to guide you through the steps
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
A more complex model
d$contrastSquare = d$contrast^2
lmer(p100~1+contrast+contrastSquare+(1+contrast+contrastSquare|subject),data = d)
Warning messages:
1: Some predictor variables are on very different scales: consider rescaling
2: In checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
3: In checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 2 negative eigenvalues
Convergence problems
Indicator
- Convergence warning (always a problem)
- random effect correlation is either 0 or 1 (very seldom correct)
- model takes very long time to fit (could be correct though)
Reasons
- misspecified or overspecified models (specified fixed variable as random variable?)
- too many parameters and not enough data,
- data have big outliers/are noisy
Your possiblities:
- clean data
- center predictors (remove mean) and scale (divide by SD of independent variable)
- use Bayesian fit and put a soft prior on the covariance structure (
MCMCglmm,rstanarm,brms) - simplify the model (parsimoneous models; Bates 2015)
The ideal case
\[ \sum = \left[ {\begin{array}{*{20}{c}} 1&{{\rho_{ab}}}&{{\rho_{ac}}}&{{\rho_{ad}}}\\ {{\rho_{ab}}}&1&{{\rho_{bc}}}&{{\rho_{bd}}}\\ {{\rho_{ac}}}&{{\rho_{bc}}}&1&{{\rho_{cd}}}\\ {{\rho_{ad}}}&{{\rho_{bd}}}&{{\rho_{cd}}}&1 \end{array}} \right]\]
y ~ 1 + A + B + C + (1 + A + B + C | group)
The simplest structure
\[\Sigma = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]\]
y ~ 1 + X1 + X2 + X3 + (1|group) + (0+X1|group) + (0+X2|group) + (0+X3|group)
shorthand:
y ~ 1 + X1 + X2 + X3 + (1+X1+X2+X3||group)
note the || instead if |
\[\Sigma = \left[ {\begin{array}{*{20}{c}} 1&{{\rho _a}}&{{\rho _a}}&{{\rho _a}}\\ {{\rho _a}}&1&{{\rho _a}}&{{\rho _a}}\\ {{\rho _a}}&{{\rho _a}}&1&{{\rho _a}}\\ {{\rho _a}}&{{\rho _a}}&{{\rho _a}}&1 \end{array}} \right]\]
Compound symmetry \(\simeq\) Repeated measures ANOVA
y ~ 1 + X1 + (1|group) + (1|group:X1)
Which one to choose?
- 1: You can estimate the full (enough data or put a lkj-prior if you are Bayes)
- 2: Prior assumption on shape and you don’t have to change it (non-contingent on data)
- 3: Simplify in a data-driven way
Ongoing debate “Keep it maximal”, Barr et al. 2013 vs. “Parsimoneous mixed models”, Bates et al. 2015
Barr promotes full models. Bates promotes a step wise reduction if effects do not significantly explain variance
Overview
- Repeated measures
- The mixed model
- An example to guide you through the steps
- Inference
- Assumption checking
- Shrinkage
- Terminology
- Convergence Problems
- Multiple random variables
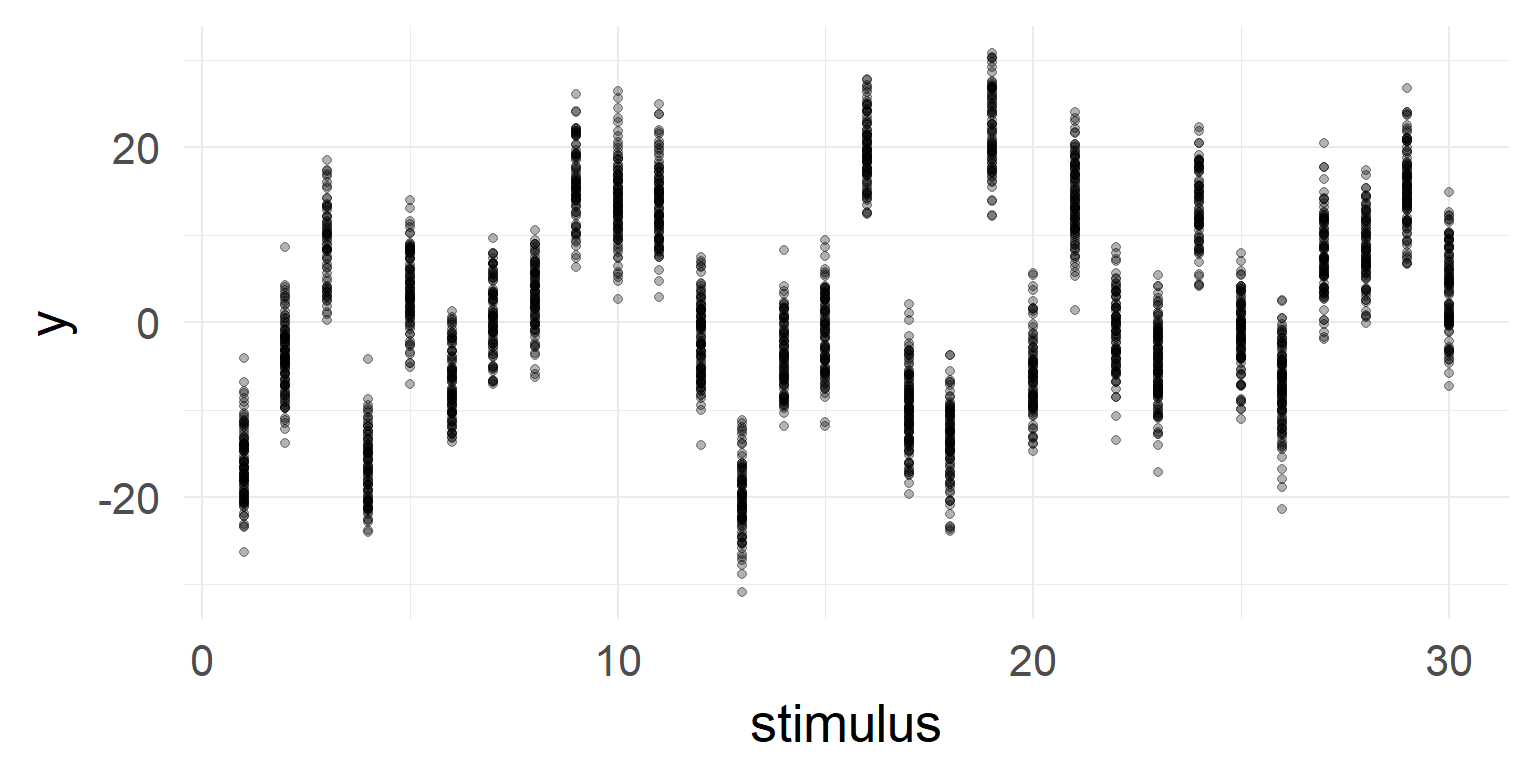
Multiple random variables
What a nice effect! Write paper and end of story?
But very high stimulus variance!
But very high stimulus variance
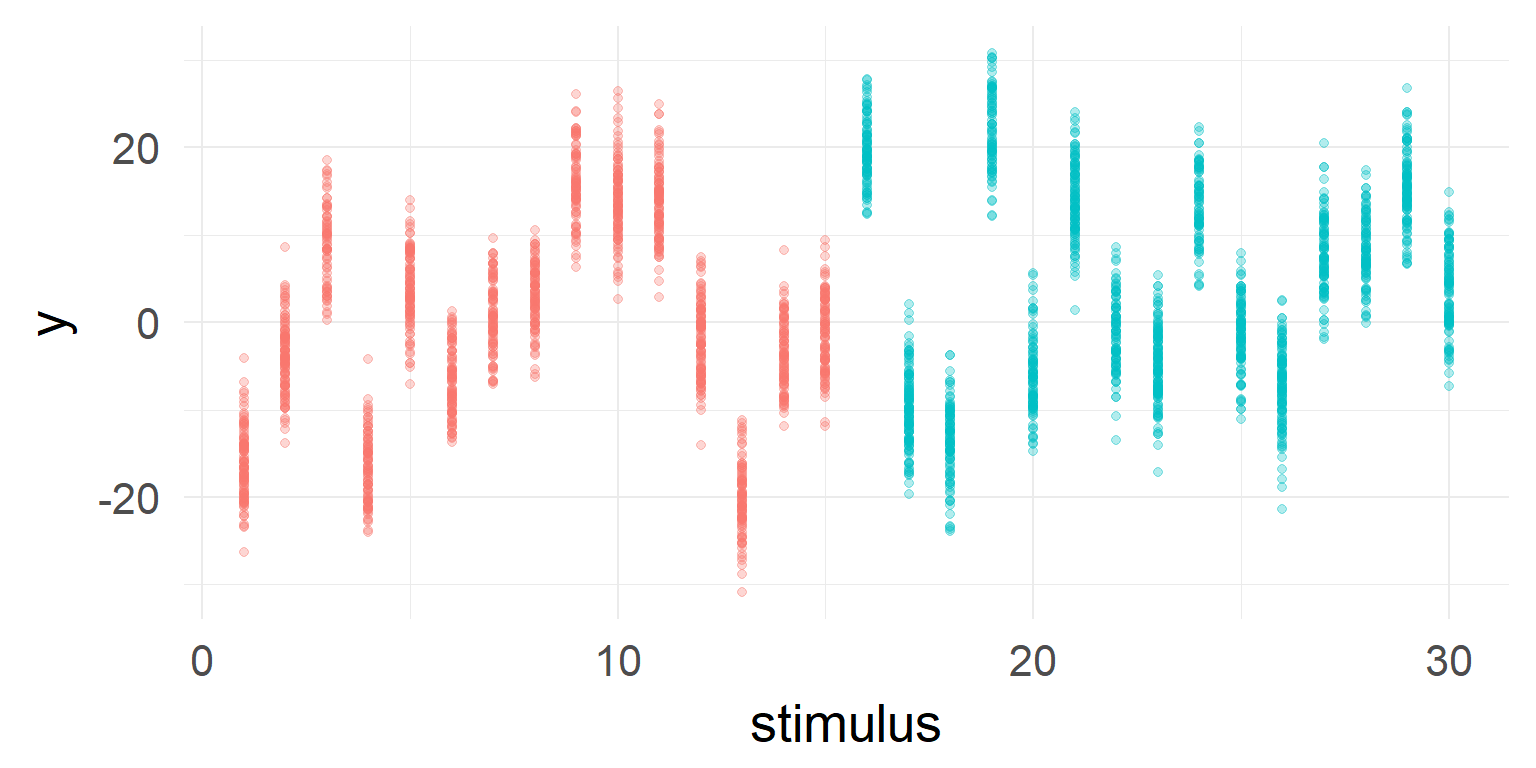
a high variance can lead to sporadic effects
You should include it in your model
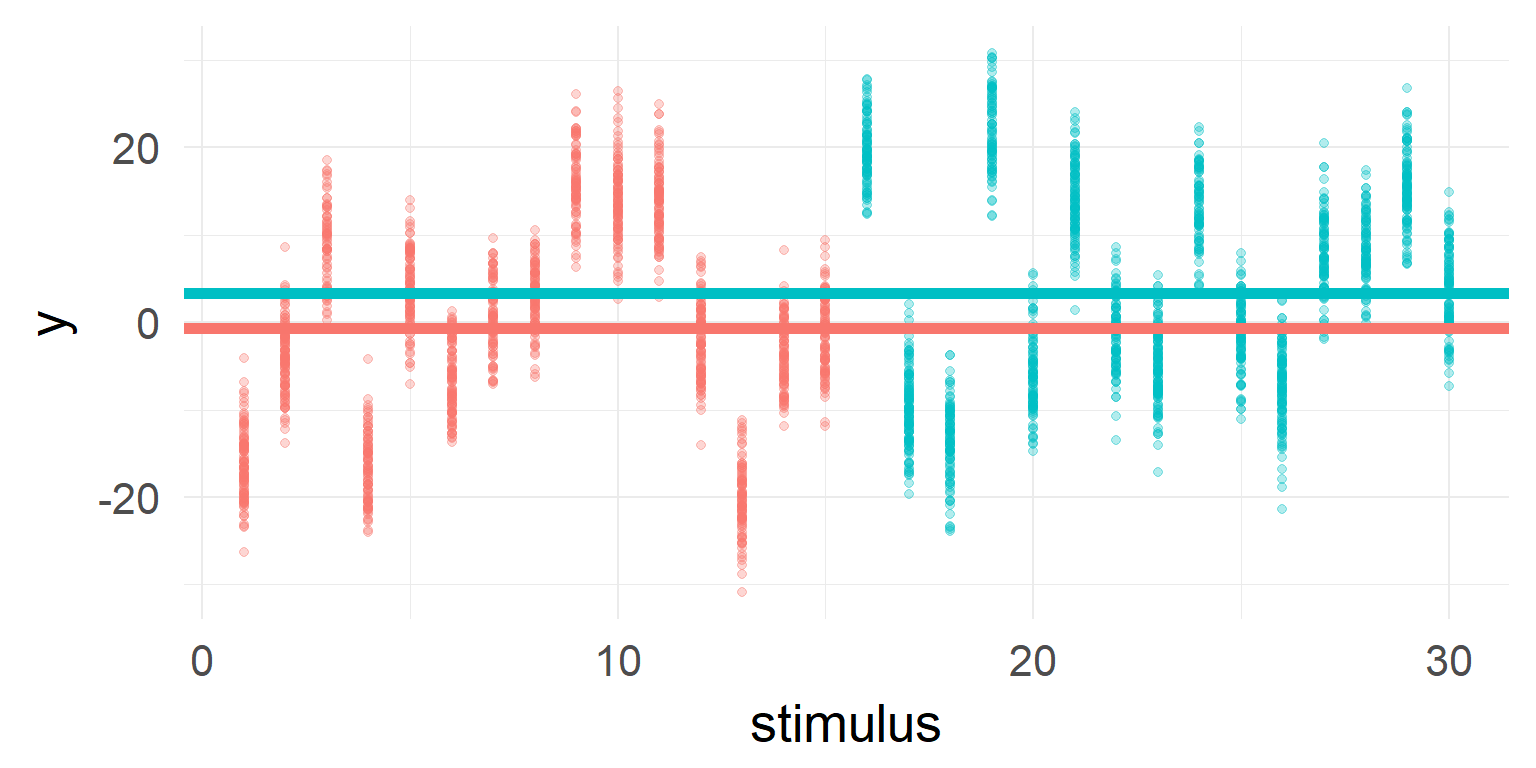
Often it is necessary to add multiple random effects! Examples are: subjects, stimuli (images, words, etc)
y ~ 1 + condA (1+condA|subject) + (1+condA|stimulus)
When to include what
Some guidance:
- Predictor is a subset of a population?
- => random/grouping variable e.g. subjects, images, words
- Predictor is within subject/grouping?
- => random coefficients
- Predictor is between subject/grouping or aggregated?
- => only fixed coefficient
Summary
- We learned how to analyze repeated measures data
- We learned how to structure random effects
- We learned how to check assumptions of Mixed Models
- We learned about shrinkage
- We learned how to include multiple random variables
Papers & Books
- FAQ on GLMMs
- Book: Data Analysis Using Regression and Multilevel/Hierarchical Models
- Book: Regression Modeling Strategies
- (advanced) Book: Richly Parameterized Linear Models: Additive, Time Series, and Spatial Models Using Random Effects
- Book on LME4
- Paper: Parsimonious Mixed Models
- Paper: Random effects structure for confirmatory hypothesis testing: Keep it maximal
- Example Study: Experimental effects and individual differences in linear mixed models: estimating the relationship between spatial, object, and attraction effects in visual attention