Slides & my Presentation style

Click this link to add notes to the slides

this adds ?showNotes=true to the file

You can download the pdf or print them yourself:

click this link for pdf printable (use google chrome)

click this link for pdf printable + notes

HTML is best viewed in chrome

What we want to be able to analyse

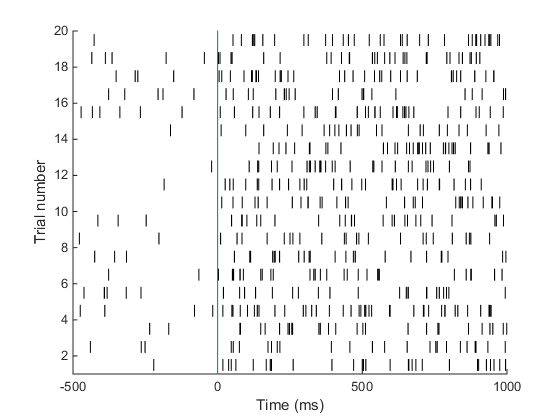Neural firing is poisson-like 1,2,3,4 .. spike / s => Discrete outcome!

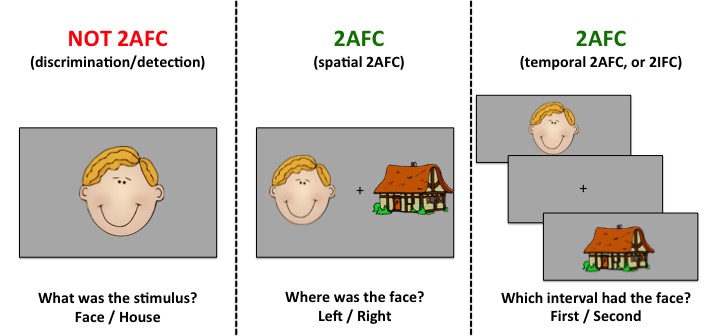Many experiments have two outcomes (more example to come)

Data is only 0 and 1, we want to estimate probabilities

GLMs allow us to model outcomes from distributions other than the normal distribution.

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

Example tasks with binomial data

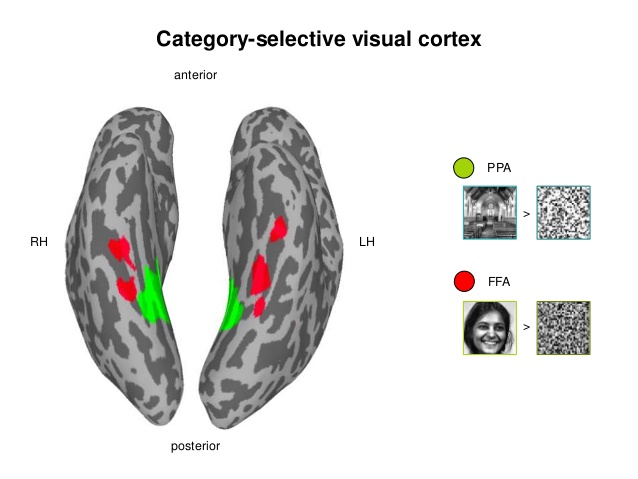
FFA vs. PPA

Decoding: Is it a face or a house? Based on BOLD/EEG data

Will the patient survive?

Contrast Gratings

Did you see a grating?

Bernoulli vs Binomial

Bernoulli

A single throw of a coin
Will the coin be heads or tails?

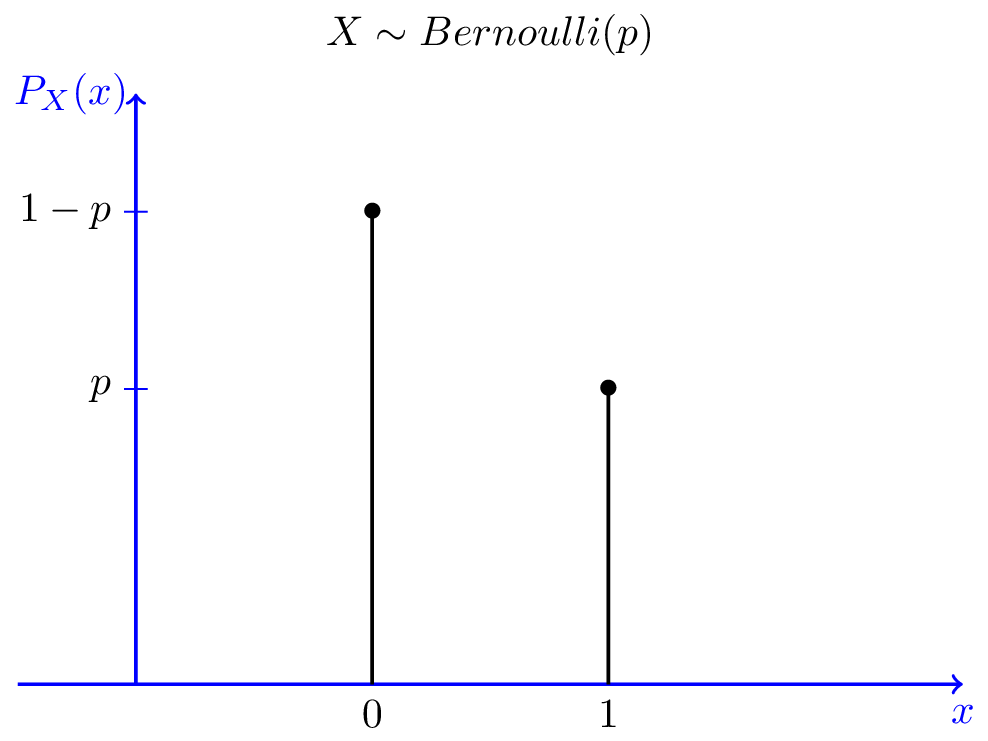
bernoulli

Binomial

Sum over multiple Bernoulli throws
How many heads will I get (out of N throws)

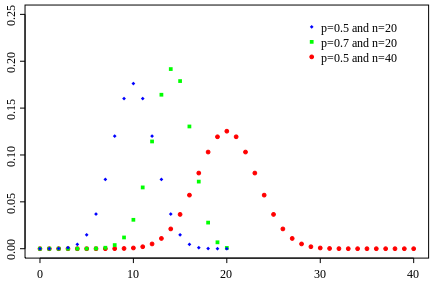
binomial

An example with a continuos variable

Task: Do you observe a grating?
Research Question: What is the minimum contrast to reliably (>25%) detect a grating?

Contrast Gratings

n.trial =150
n.contrastLevels=12

The Data

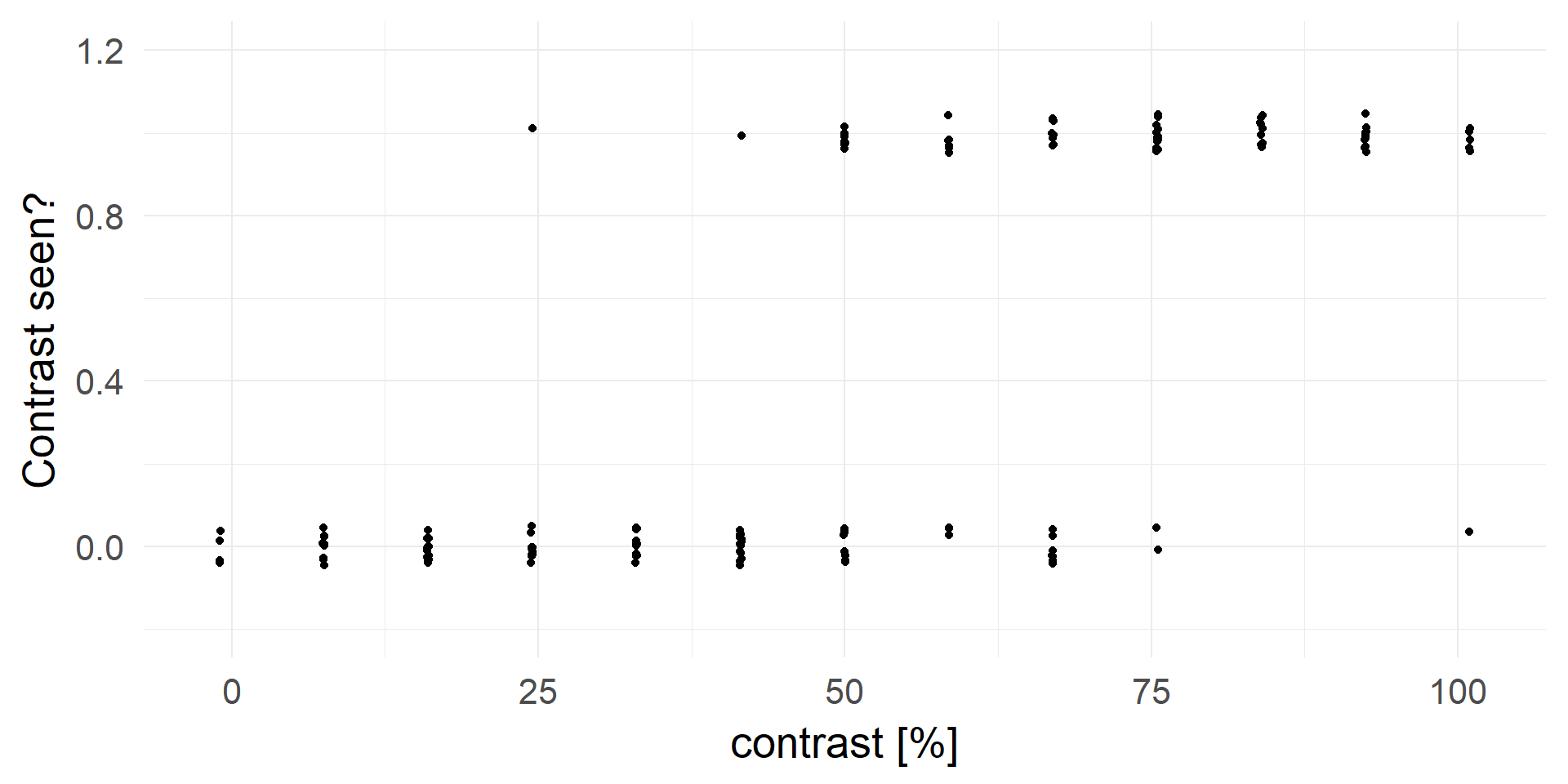
What is the probability to detect the target?

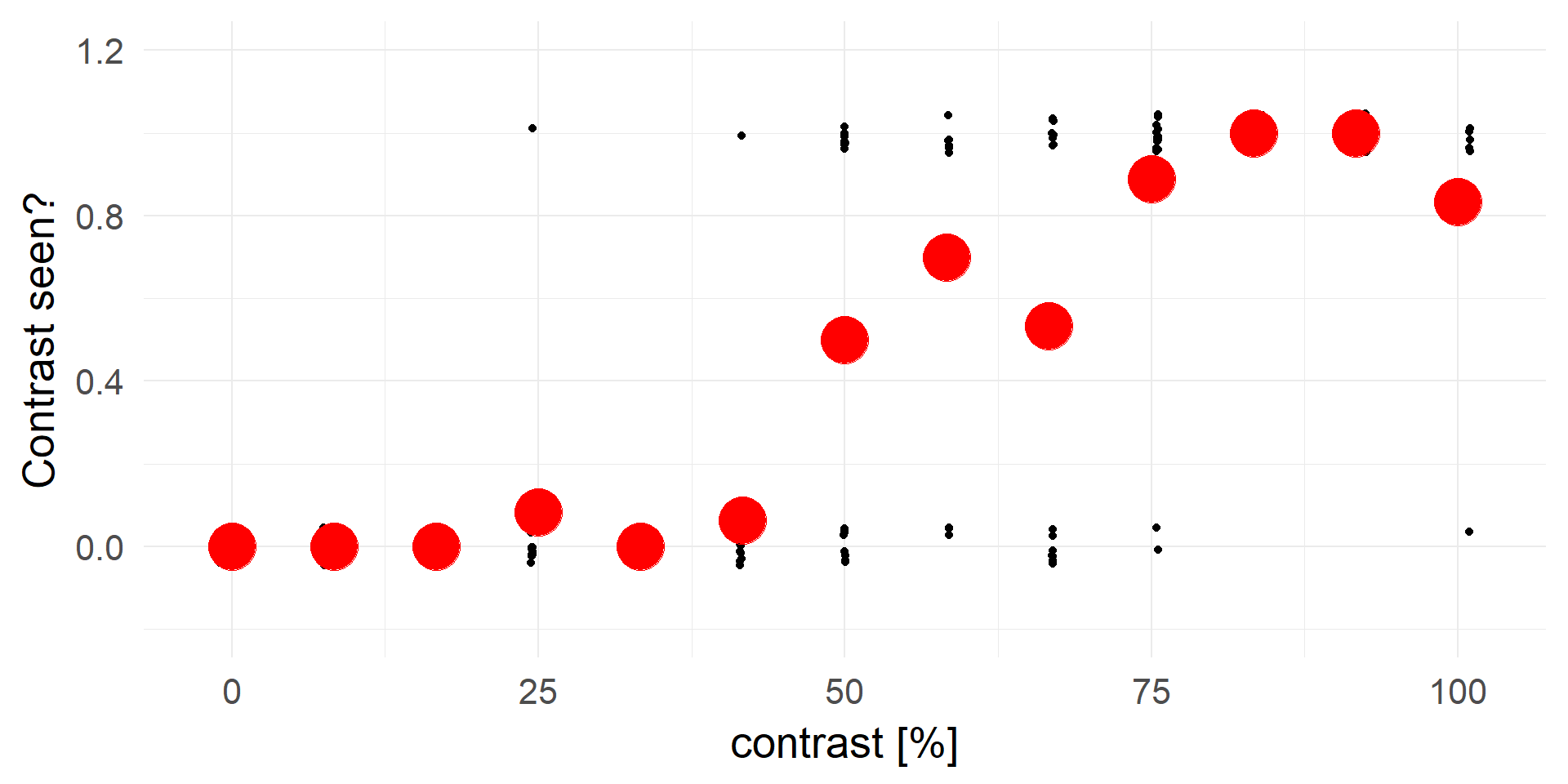
Let’s try linear regression

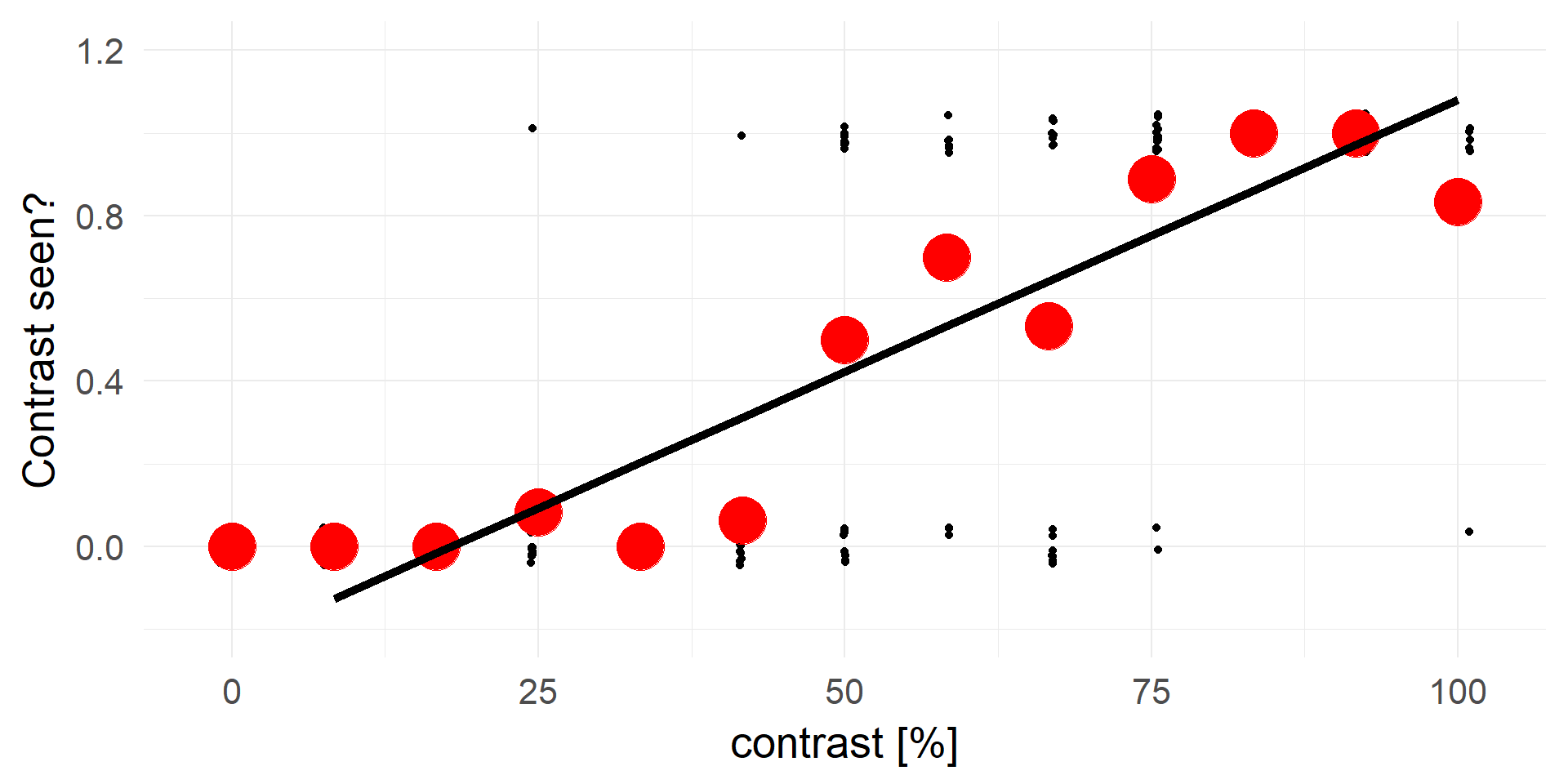
There are no negative probabilities. What to do?

Truncating everything smaller 0 / larger 1:

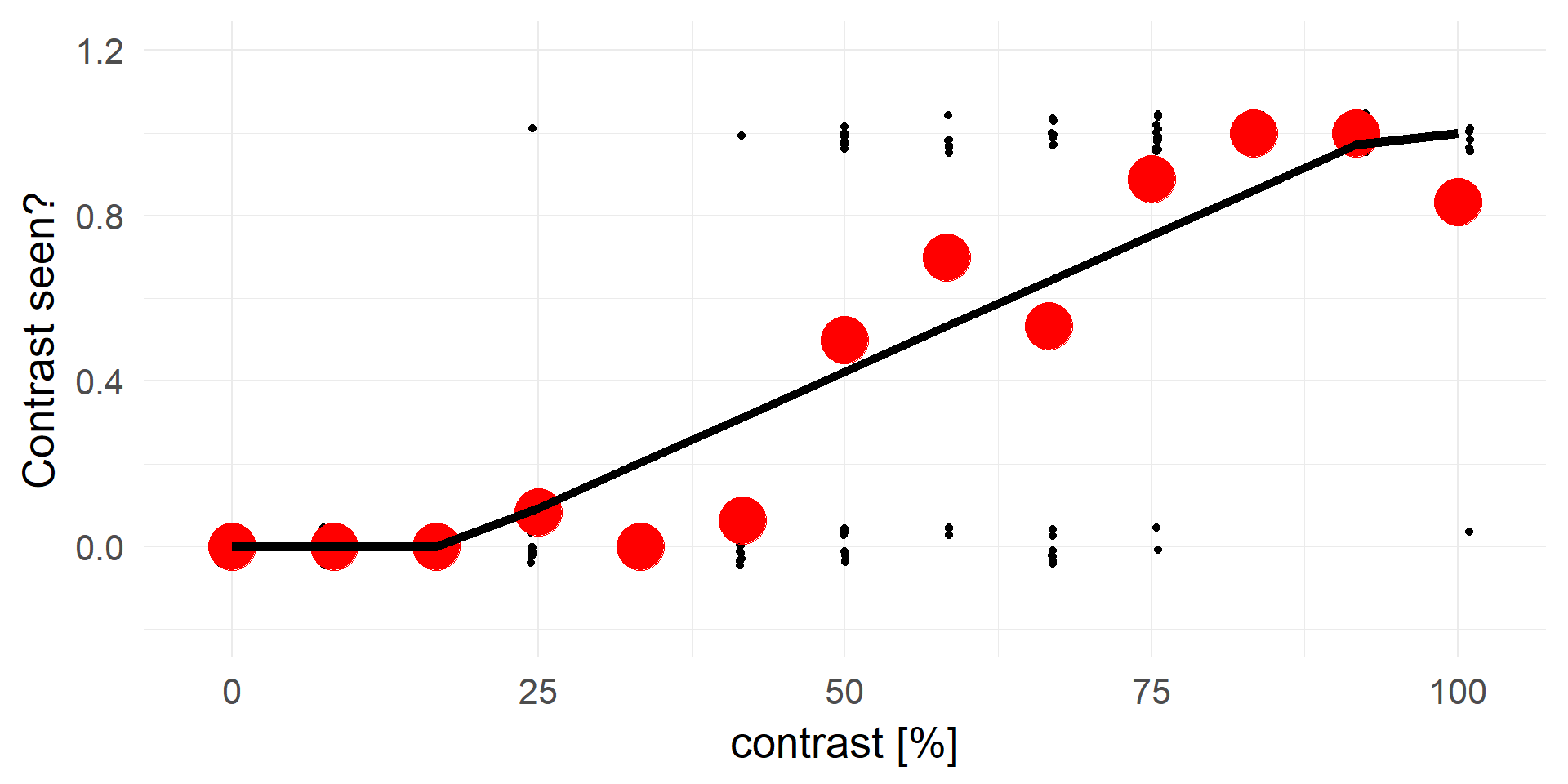
A contrast of ~16% will be rejected in 100% of cases.

A strong statement!

A better fit

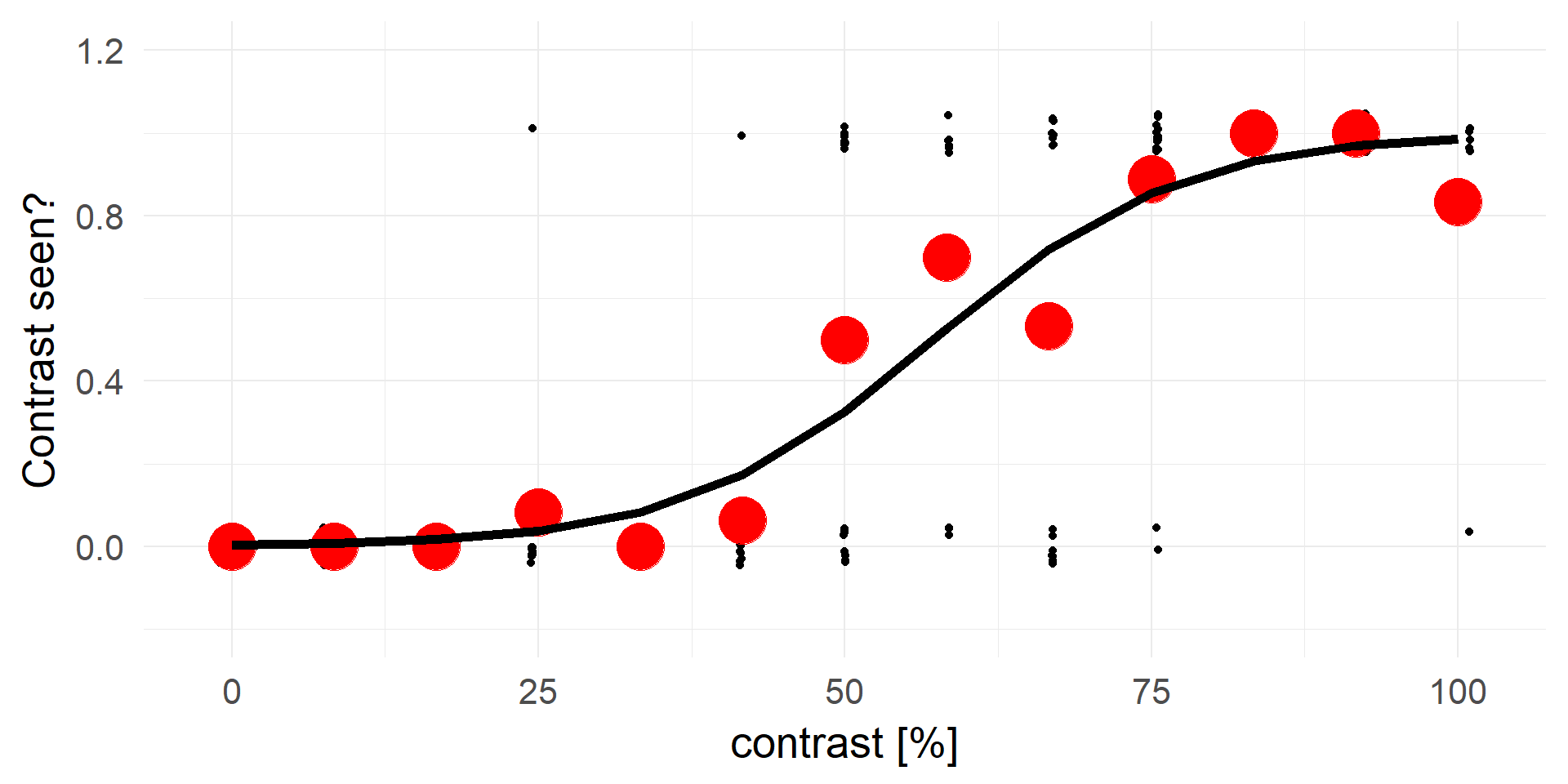
transforming y

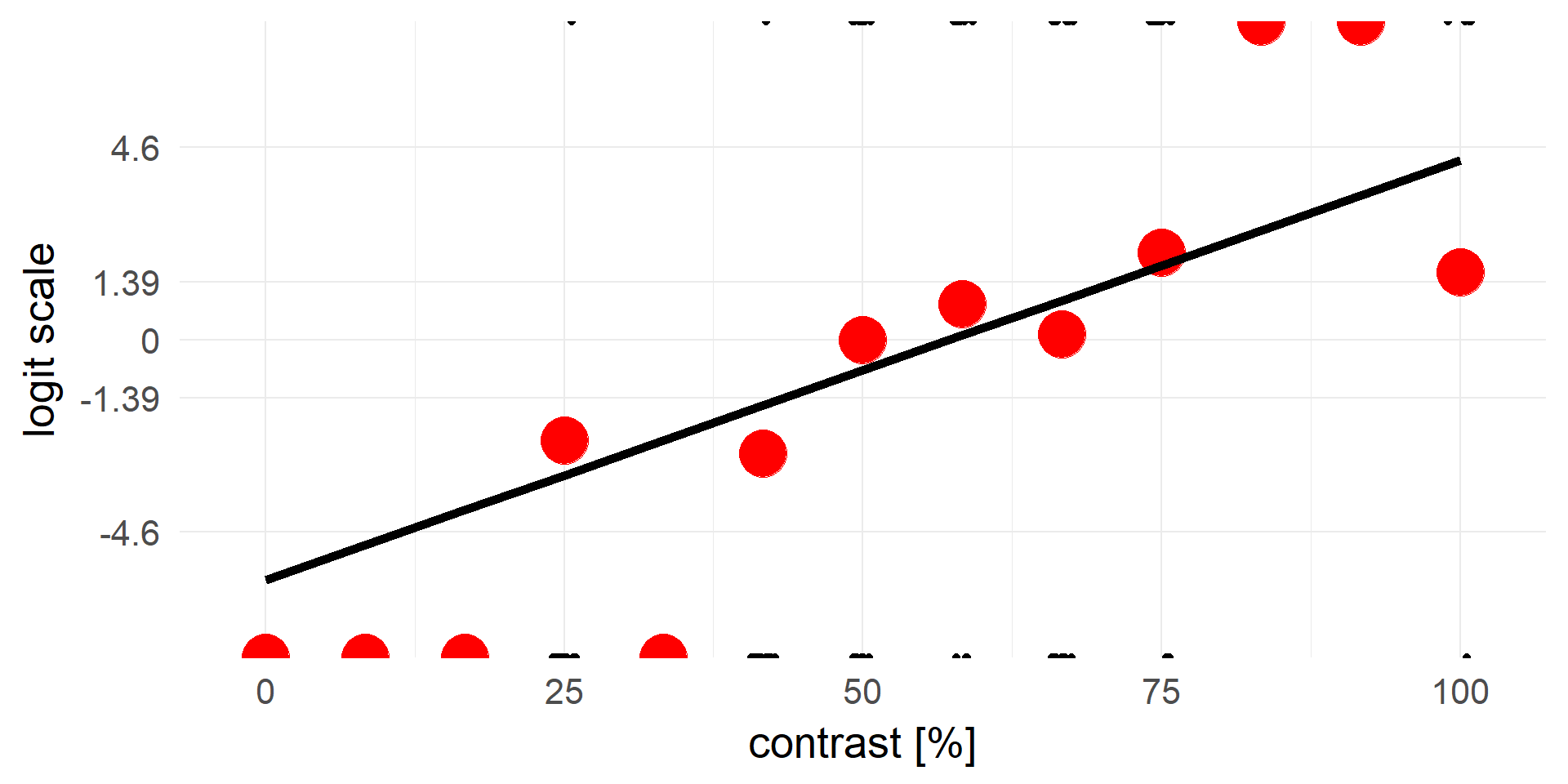
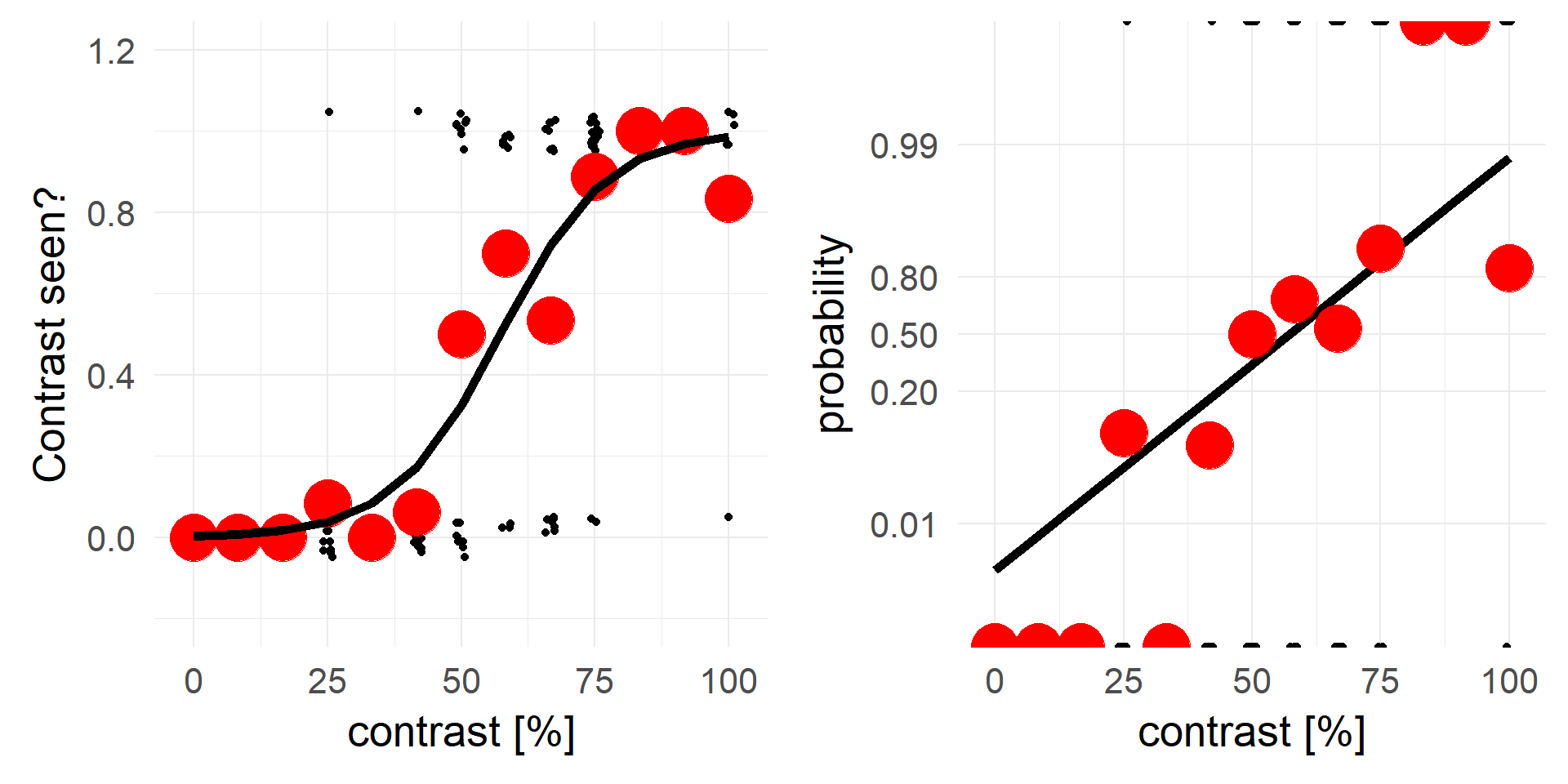An alternative view, same data but different y-axis

logit & inv.logit

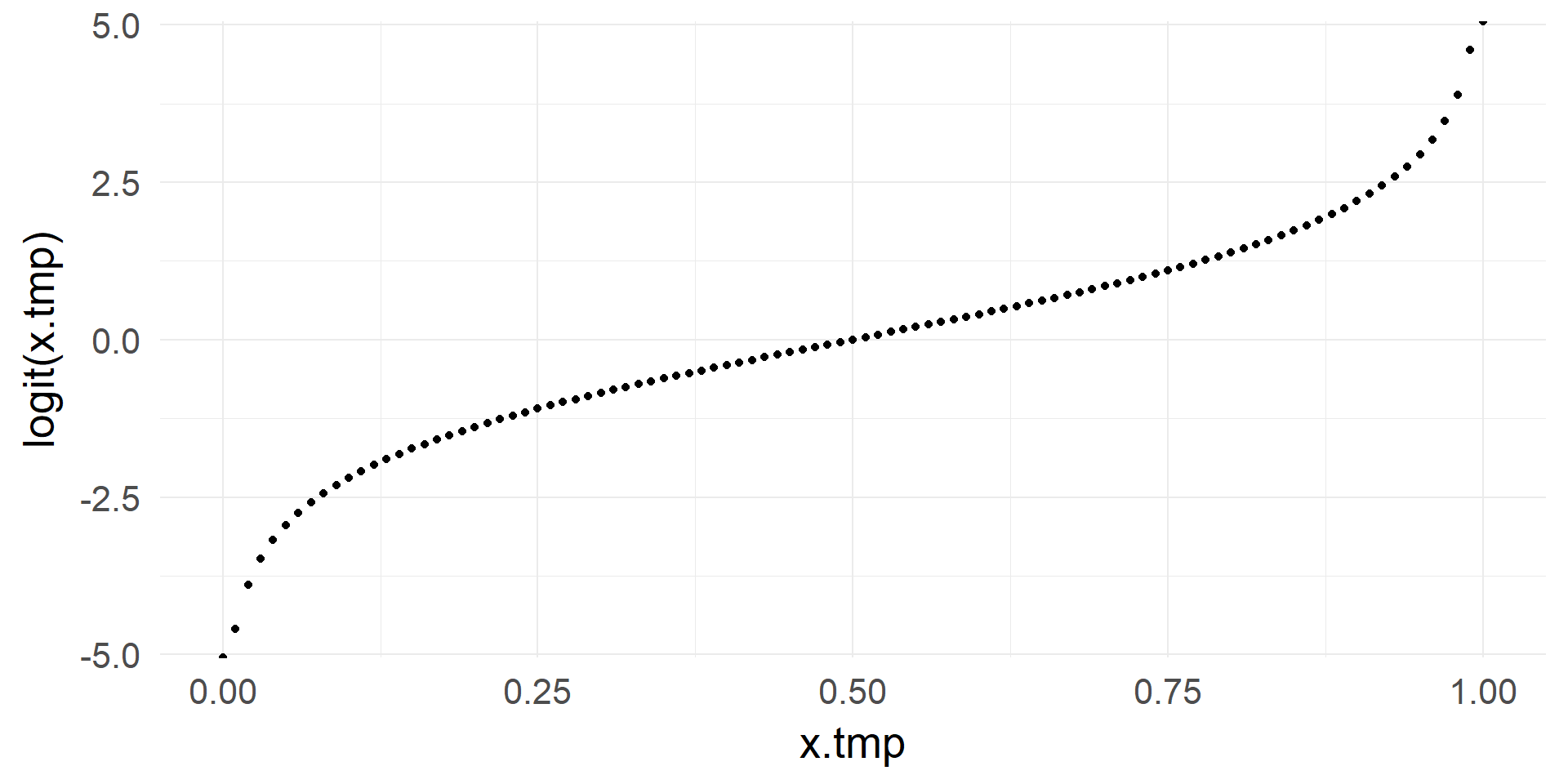
From \([0, 1]\) to \([-\infty, +\infty]\)

\[ x = log(\frac{p}{1-p})\]

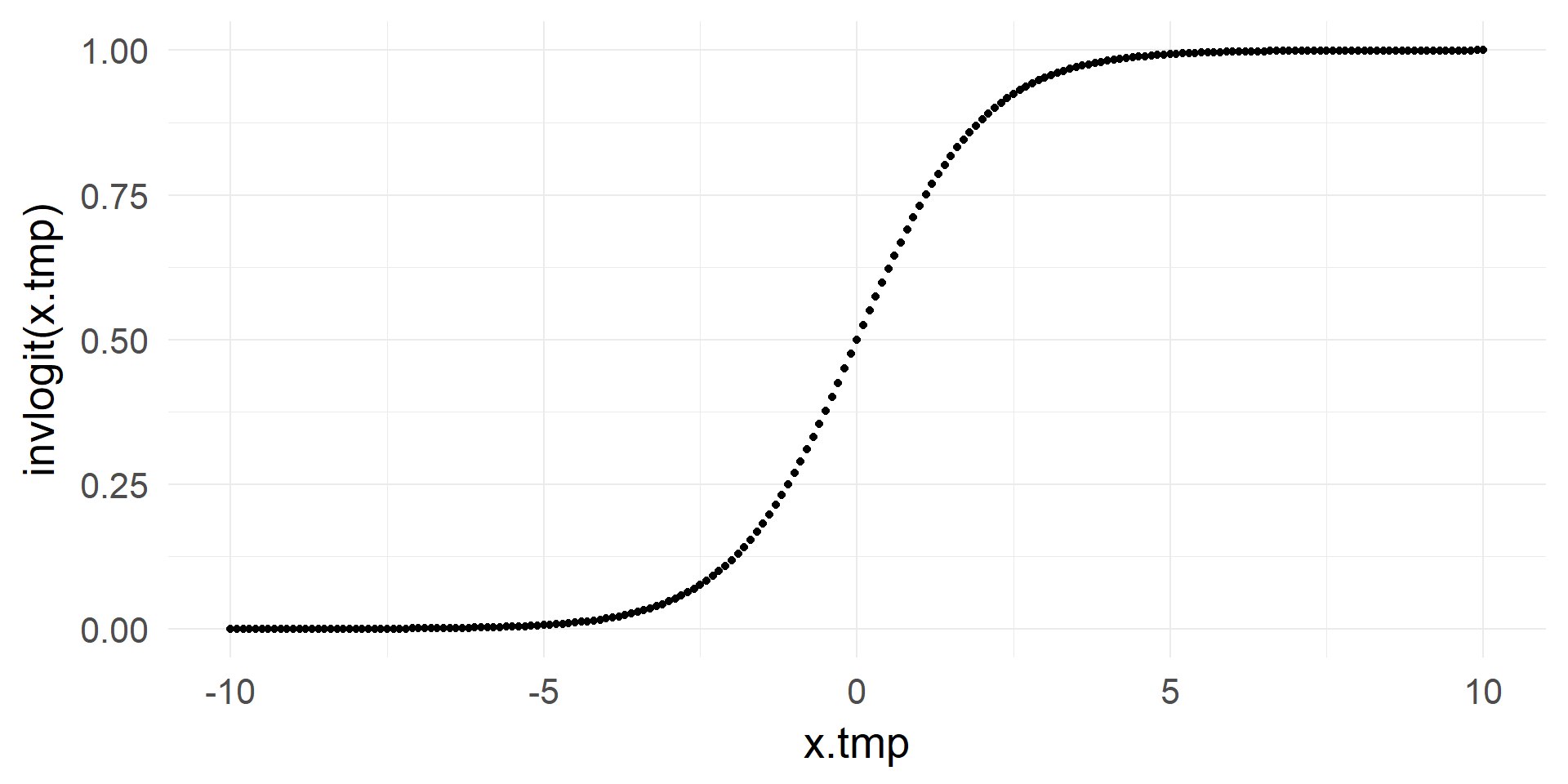
From \([-\infty, +\infty]\) to \([0, 1]\)

\[ p = \frac{1}{1+e^{-x}}\]

The domain we are working in goes from \(-\infty\) to \(+\infty\). We assume our relationships are additive in this domain

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

logistic regression

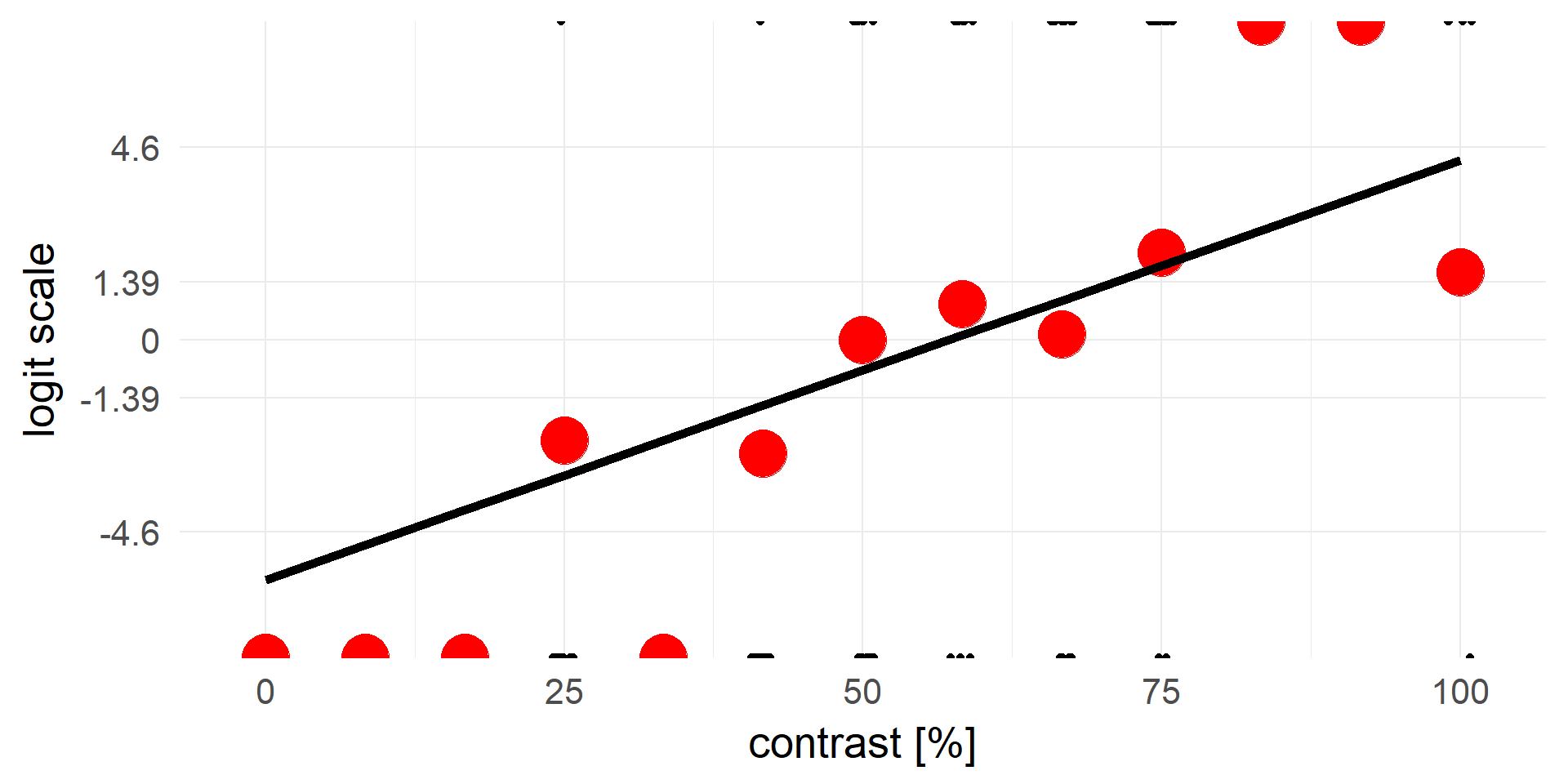
\(y = invlogit(X\beta + e)\) <=> \(logit(y) = X\beta + e\)

\[y = g^-1( X\beta + e) \]

yes! that is the g from GLM

We call this logistic regression

Running a logistic regression in R

res = glm(formula = response ~ 1 + contrast, data=d,family=binomial)
summary(res)

## 
## Call:
## glm(formula = response ~ 1 + contrast, family = binomial, data = d)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.9298  -0.4171  -0.1217   0.5597   2.5579  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -5.73617    0.91880  -6.243 4.29e-10 ***
## contrast     0.10014    0.01556   6.437 1.22e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 205.78  on 149  degrees of freedom
## Residual deviance: 103.39  on 148  degrees of freedom
## AIC: 107.39
## 
## Number of Fisher Scoring iterations: 6

It is straight forward to run (but not interprete) a logistic regression in R. We exchange lm by glm and specify the family of the data - in our case binomial data. This runs a logistic regression.

As you can see in the output of R, we get coefficients again. Important: These coeffcients are in logit-space - they have no straight relationship to probabilities (we will see what the relationship is in a second). But appreciate, that you again get a an estimate for each coefficient and an uncertainty measure (Std. Error) again. You also get Walds-test significance. Why z and not t? this stack exchange might help but is mathematically more involved. It has to do with a later concept that we will get to know at the end of the lecture (the relationship between the mean value and the respective residual variance).

We will learn later what the lines (Dispersion parameter for binomial family taken to be 1) and Null deviance/Residual deviance mean.

the interplay of our two predictors

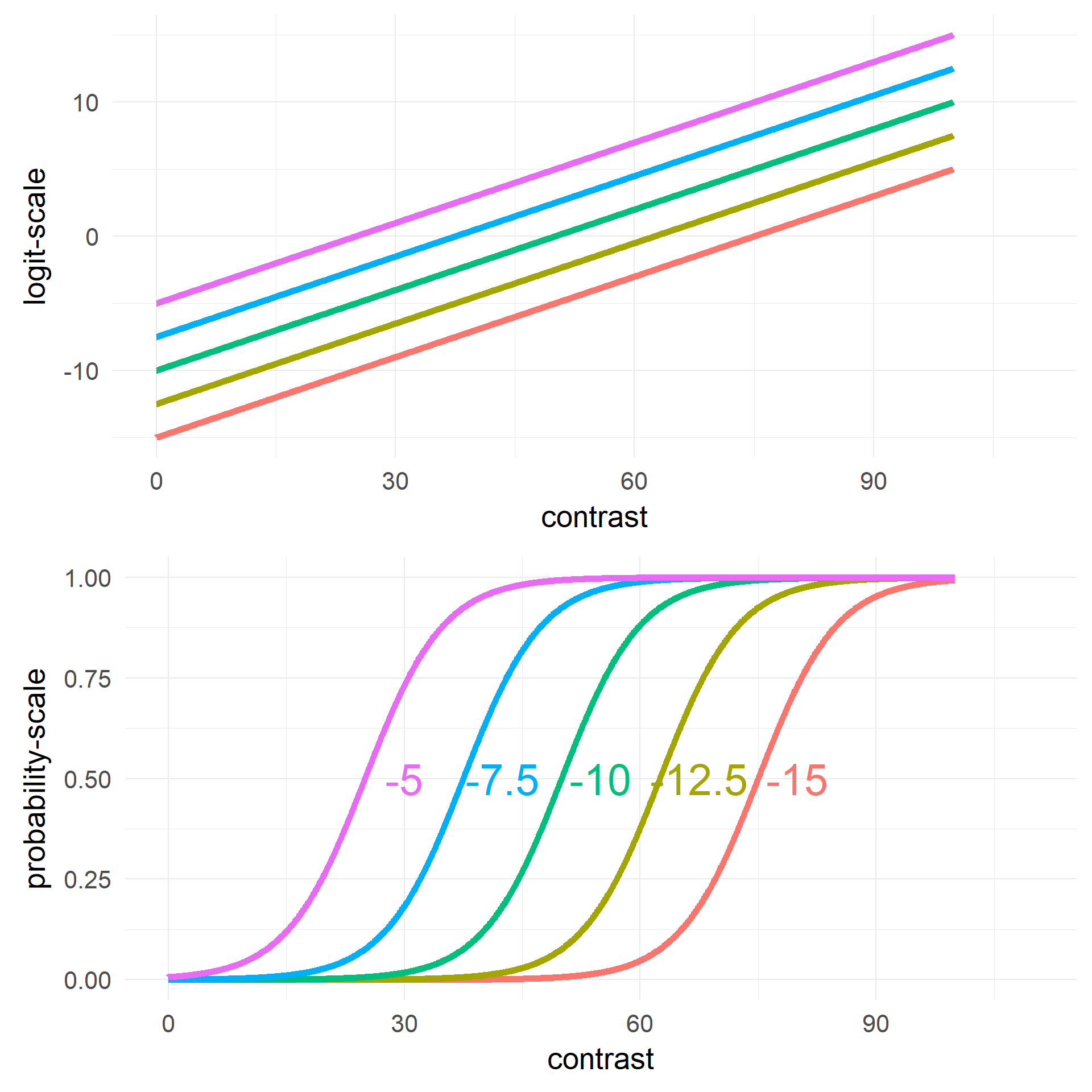
Changing Intercept \(\beta_0\)

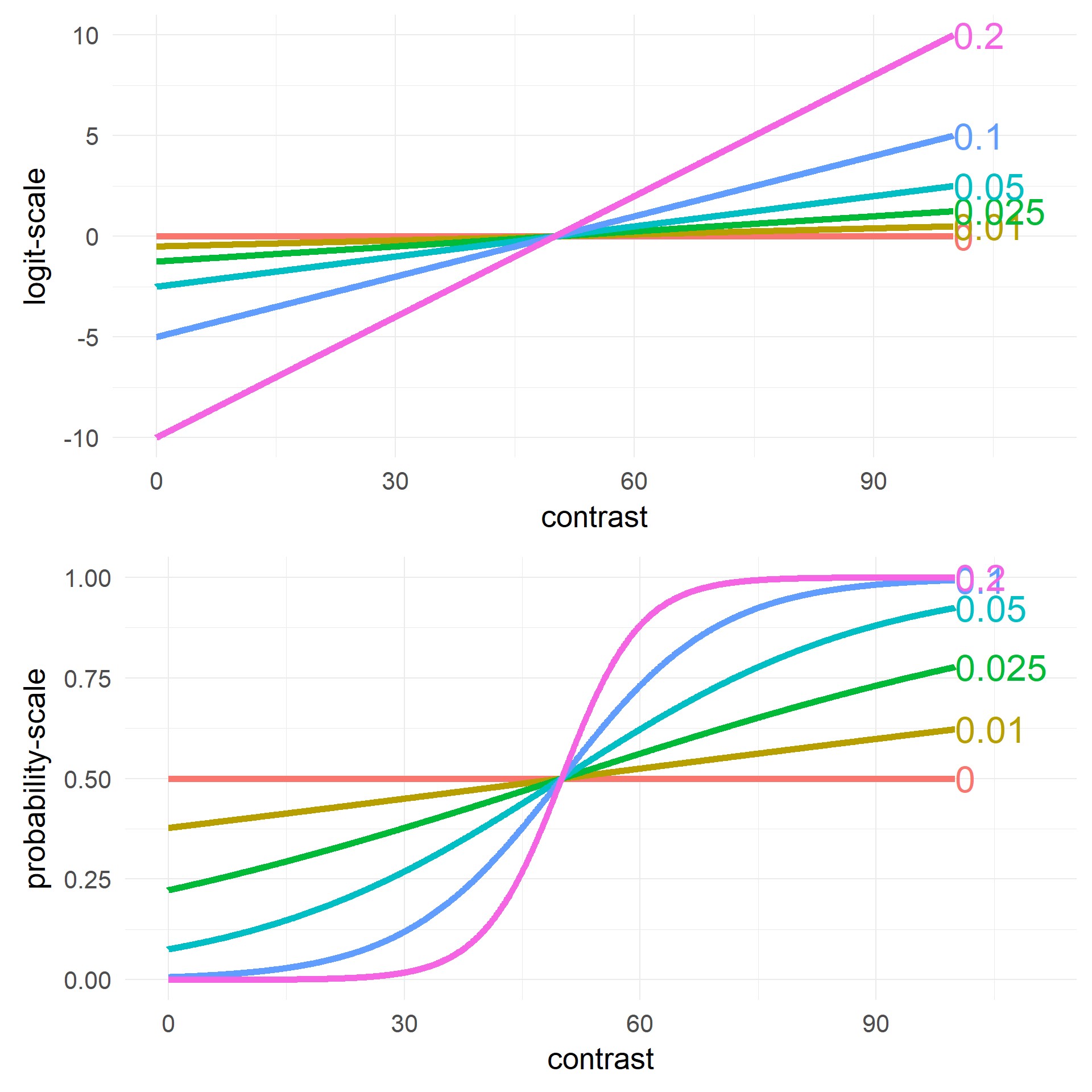
Changing Slope \(\beta_1\)

\[y = g^-1(\beta_0 + X_1\beta_1 + e) \]

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

What are the units on the y-axis / the coefficients?

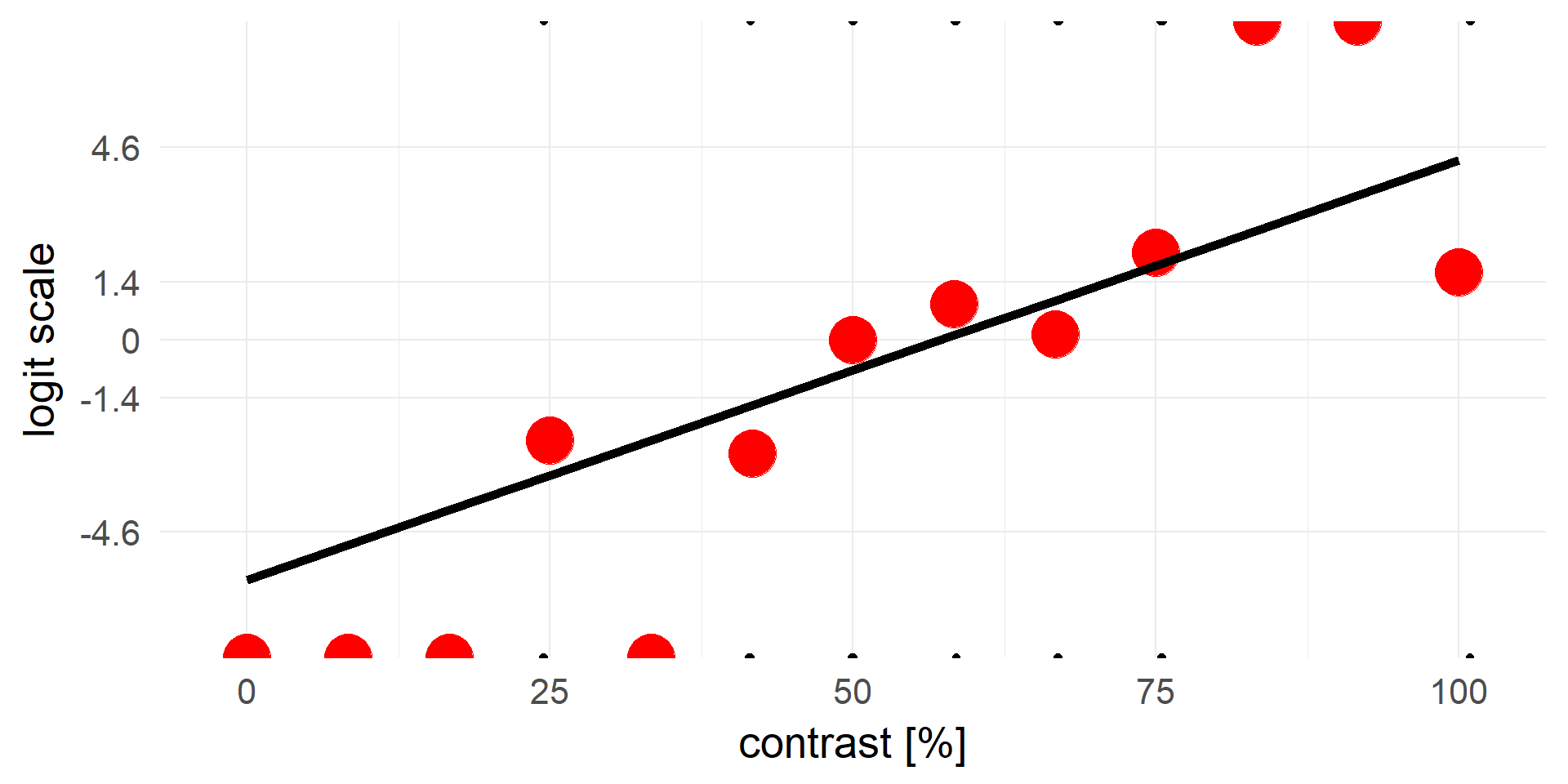\[invlogit = \frac 1 {1+e^{-x}}\]

\[logit = log(\frac p {1-p}) = log(odds)\]

The logit function is of most interest here. If we look at it, it for has two components, the log() and the \(\frac p {1-p}\).

What are odds?

Odds are a somewhat unintuitive quantity: \[p(coxi==nerd) = 0.75\]

\[odds(coxi==nerd) = \frac{p(coxi==nerd)}{p(coxi \neq nerd)} = \frac{0.75}{1-0.75} = \frac{0.75}{0.25} = 3\]

In words: the odds for an cogsci to be a nerd are 3 to 1

For 3 nerd coxis you will find 1 non-nerd

Odds are unintuitive, they are useful to understand because they (or the log version of them) are the thing that the logistic regression models. They also have nice symmetry properties. If you are a notorious gambler you might have heared of odds before, if not the principle is easy: You divide a probability that something is happening by the probability it is not hapenning.

For instance, you have a 0.25% chance that the horse you are betting on will win. That gives you odds of 0.25 / 0.75 => 1 : 3 (odds of one to three). Note how this is symmetrical to a 75% chance, where the odds would be 3:1 (more to that in the section of relative risks). In gambling this quantitiy is used by the bookmaker, because it directly tells you how much you will win: if you invest 1€ you will win 3€ (the money you GAIN would be 3€ + 1€ (1€ you paid for the gamble)).

Unfortunately there is not a single good way to interpret the logistic regression parameters and we will see why in a second.

A closer look at the logit function

\[odds = \frac{p}{1-p}\] (\(odds \in [0,+\infty]\), halfway there)

taking the log()

\[log(odds) = logit = log(\frac{p}{1-p})\]

This is a mapping from \(p \in [0,1]\) to \(logit(p) \in [-\infty +\infty]\)

Background: Differences in probabilities, relative risk vs risk difference

\(p(coxi==nerd) = 0.75\)

\(p(psycho==nerd) = 0.6\)

Risk Difference: 0.75 - 0.6 => coxis are 15 percentage points more likely to be nerds

Relative Risk: \(\frac{0.75}{0.6} = 1.25\) => Coxis are 25% more likely to be nerds

Relative Risks are intuitive but non symmetric:

\(\frac{p(X)}{p(Y)} = \frac{0.99}{0.98} = 1.01\) => X is 1% more likely than Y

\(\frac{p(\neg X)}{p(\neg Y)} = \frac{0.01}{0.02} = 0.5\) => not X is 50% more likely than not Y

The problem with relative risks

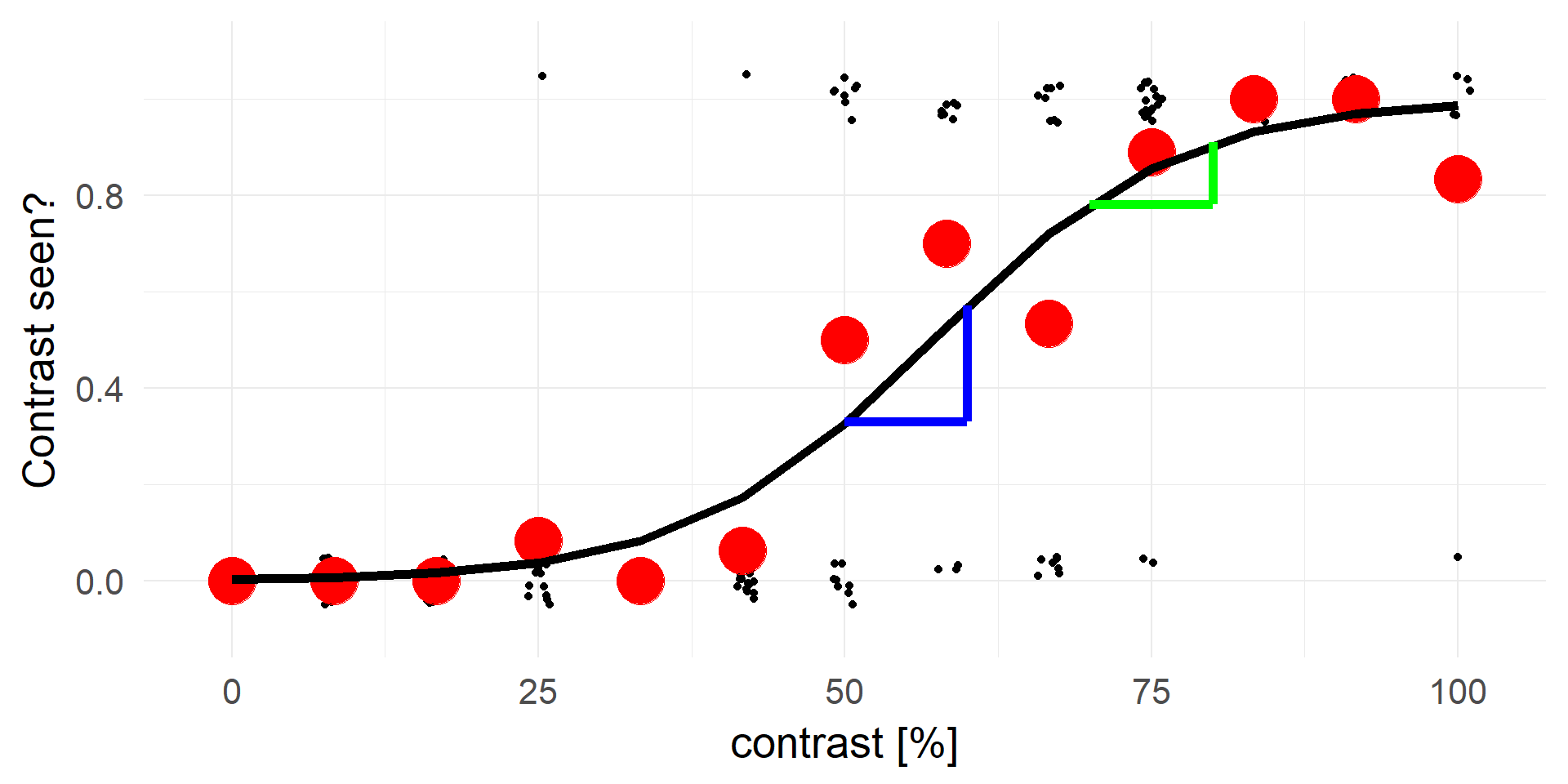p(X|contrast=60) / p(X|contrast=50) = 0.57/0.33 = 1.73

p(X|contrast=80) / p(X|contrast=70) = 0.91/0.78 = 1.17

An contrast increase of 10 on X is not a constant increase in the relative risks.

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

The constant / Intercept

TLDR; \(\beta_0\) = log-odds if everything else is 0.

\(\beta_0\)<0: \(p = invlogit(-) < 0.5\)

\(\beta_0\)==0: \(p = invlogit(0) = 0.5\)

\(\beta_0\)>0: \(p = invlogit(+) > 0.5\)

\(y(x) = invlogit(\beta_0 + \beta_1 x)\)

\(y(x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x)}}\)

\(y(x=0) = \frac{1}{1 + e^{-\beta_0}}\)

In our example

coef(glm(response~contrast,data=d,family=binomial))[1] # log-odds

## (Intercept) 
##   -5.736166

invlogit(coef(glm(response~contrast,data=d,family=binomial))[1]) # probability

## (Intercept) 
## 0.003216738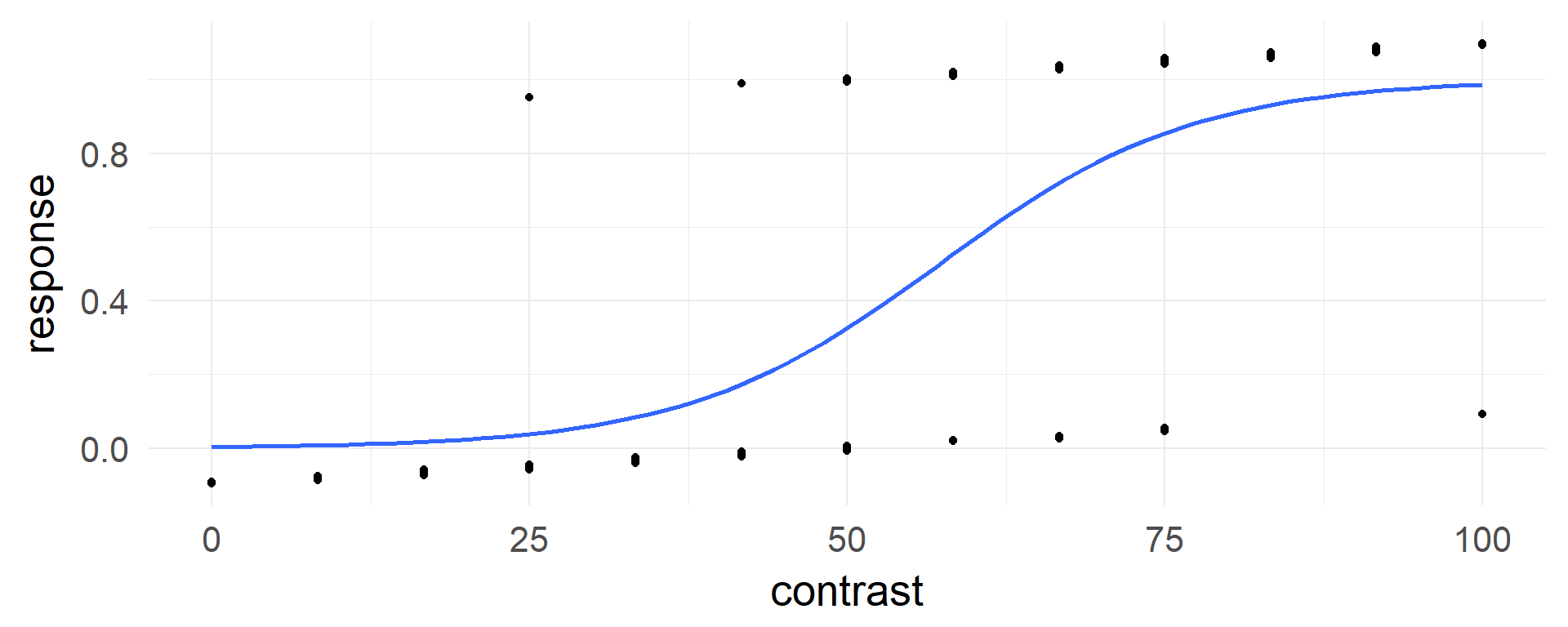

Interpreting the slope

TLDR; \(\beta_1\) = how much a change of x+1 increases the log(odds-ratio)

\[log(odds) = \color{red}{logit(\hat y(x))} = \beta_0 + \beta_1 x \]
An increase by \(1*\beta_1\) : \(\color{green}{logit(\hat y(x+1))} = \beta_0 + \beta_1 (x+1)\)

Taking the difference:

\[\color{green}{logit(\hat y(x+1))} - \color{red}{logit(\hat y(x))} = \color{green}{\beta_0 + \beta_1 (x+1)} - (\color{red}{\beta_0 + \beta_1 x} )= \beta_1 \]
Using the log-rule on the left side (\(log(odds_a) - log(odds_b) = log(\frac {odds_a} {odds_b} )\))

\[\beta_1 = \color{green}{logit(\hat y(x+1))} - \color{red}{logit(\hat y(x))} = \color{green}{log(odds(x+1)} - \color{red}{log(odds(x))}= log(\color{blue}{\frac{odds(x+1)}{odds(x)}})\]
\[\beta_1 = log(\color{blue}{odds-ratio})\]

What are odds-ratios?

\[odds(coxi==nerd) = 3\]

\[odds(psycho==nerd) = 1.5\]

\[odds-ratio = \frac{3}{1.5} = 2\]

The odds that coxis are nerds are 2x as high than the odds that psychology students are nerds.

(remember relative risk: Coxis are 1.25 as likely than psychology students to be nerds)

\[e^{\beta_1} = odds-ratio( y(x)/y(x+1))\]

The odds that you will succeed are \(e^{beta}\) higher at \(y(x+1)\) than \(y(x)\)

Back to the example

co = coef(glm(response~contrast,data=d,family=binomial)) # log-odds ratio
co["contrast"]

##  contrast 
## 0.1001421

exp(co["contrast"]) # odds ratio

## contrast 
## 1.105328

With a step of 1, the odds change by ~1.1

With a step of 10, the odds change by ~2.7

Coming back to relative risks

Interpretation of odds ratios is difficult and unintuitive. I always try to give examples, i.e. what is the relative risks between two outcomes.

What is the relative risk between contrast = 50 and contrast = 80?

a = invlogit(co["(Intercept)"]+co["contrast"] * 80)
b = invlogit(co["(Intercept)"]+co["contrast"] * 50)

we have ~280% more successes at contrast = 80 than at contrast = 50

Intermediate Summary

\[y = g^-1(\beta X + e) \]

\(y = invlogit(\beta X + e)\) <=> \(logit(y) = \beta X + e\)

Binary data (0/1, True/False)
Units are log(odds)
one of many link-functions of GLMs
It is possible to use other functions that map \(p \in [0,1]\) to \(logit(p) \in [-\infty +\infty]\), e.g. probit (cumulative normal). But the units are not as easily interpretable as odds (!)

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

Residuals

res = glm(formula = response ~ 1 + contrast, data=d,family=binomial)
summary(res)

## 
## Call:
## glm(formula = response ~ 1 + contrast, family = binomial, data = d)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.9298  -0.4171  -0.1217   0.5597   2.5579  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -5.73617    0.91880  -6.243 4.29e-10 ***
## contrast     0.10014    0.01556   6.437 1.22e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 205.78  on 149  degrees of freedom
## Residual deviance: 103.39  on 148  degrees of freedom
## AIC: 107.39
## 
## Number of Fisher Scoring iterations: 6

Excourse Likelihood function

Deviance / Residuals

\(\theta_i = \hat{y}_i = invlogit(\beta X)\)

\(LL(y|\hat y) =\) loglikelihood \(=log(\prod{\hat{y_i}^{y_i} (1-\hat{y_i})^{(1-y_i)}})\)
for a single data point simplifies to
if \(y_i = 1\): \(log(\hat{y_i})\) if \(y_i = 0\): \(log(1-\hat{y_i})\)
Deviance Residuals: \(d_i = s_i\sqrt{-2LL(y_i|\hat y_i)}\) \(s_i = 1\) if \(y_i = 1\), \(s_i = -1\) if \(y_1 = 0\)
Intuition words: deviance is a measure of how well the model fits a data point.

For many models we use, we can explicitly write down the function. This is what we do in the second line on this slide. In logistic regression we have only one\(^*\) parameter \(\theta\) (note that on the slide is equivalently used \(\hat y_i\). If we observe a 1, the likelihood is the probability: \(\theta\), if we observe a 0, the likelihood is the probability \(1-\theta\). \(\theta_i^{y_i} (1-\theta_i)^{(1-y_i)}\) is just a clever way to write it. Because we have multiple outcomes, the probability to get exactly these outcomes is simply their multiplication (here you can see that we need the independence of outcomes assumption!). Now the log-trick comes: Multiplications are hard to do. If you take the log, they will result in additions. A sum is a lot easier to work with, and thus we usually will calculate the loglikelihood.

Deviant residuals help us to see, whether we observed outcomes that are very unlikely given our model fit. For example, if you predict a 1 only with a probability of 0.001, but observe one, you want a high value. The formula \(d_i = s_i\sqrt{-2LL(y_i|\hat y_i)}\) gives you directly that. Its a weighted version of the loglikelihood. Because the likelihood is agnostic to the outcome, we add the \(s_i\) term in front, to split 0 and 1s to \(-\) and \(+\) values.

\(^*\) note this is somewhat confusing, the likelihood has only a single parameter, but this parameter changes depending on our predictor-values. E.g. in the contrast example: \(\theta = \beta_0 + contrast*\beta_1\)

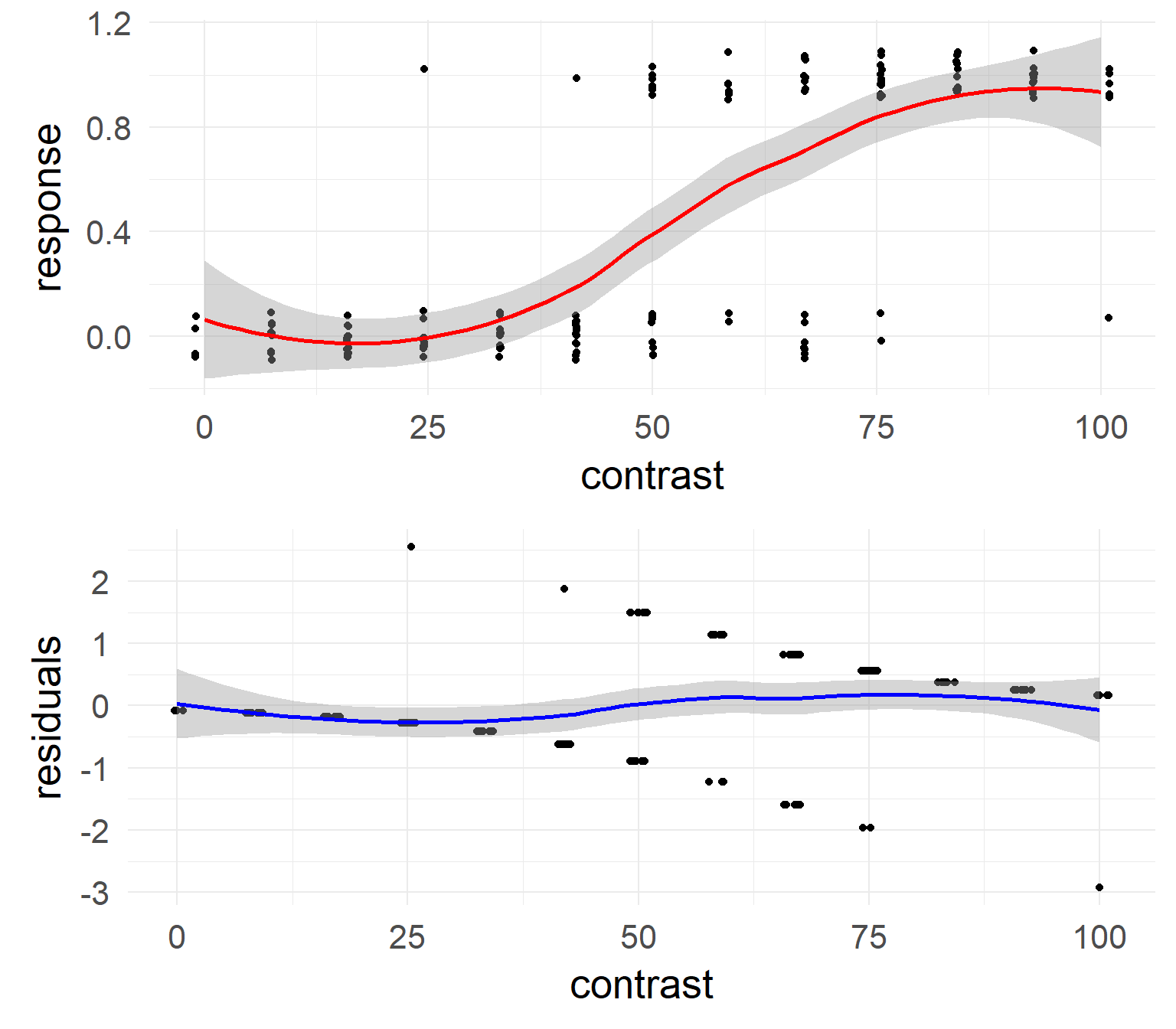
Null & Residual Deviance

res = glm(formula = response ~ 1 + contrast, data=d,family=binomial)
summary(res)

## 
## Call:
## glm(formula = response ~ 1 + contrast, family = binomial, data = d)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.9298  -0.4171  -0.1217   0.5597   2.5579  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -5.73617    0.91880  -6.243 4.29e-10 ***
## contrast     0.10014    0.01556   6.437 1.22e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 205.78  on 149  degrees of freedom
## Residual deviance: 103.39  on 148  degrees of freedom
## AIC: 107.39
## 
## Number of Fisher Scoring iterations: 6

Null Deviance\(^2\): \(2(LL(M_{saturated}) - LL(M_0))\)

Residual Deviance\(^2\): \(2(LL(M_{saturated}) - LL(M_1))\)

We are now ready to understand null and residual deviance. is the difference of log likelihoods (thus the ratio of likelihoods) A saturated model, is a model with as many parameters as outcomes (in logistic regression, this is always 0, because each outcome 0 or 1 can be matched by an exact paramter \(\theta\) of 1 or 0, in other GLMs it is not). \(LL(M_0)\) is a model with just an intercept. The loglikelihood is alway negative (or 0), thus we get a positive term for the null deviance. The null deviance basically tells us, what the likelihood of the simplest model of the data is. If we model useful things with the other predictors, the residual deviance should be smaller (that is, the loglikelihood should be larger). the residual deviance is the \(LL(M_1)\), the likelihood of our full model. Eyeballing these two numbers gives you an estimate, whether your model partially can explain the data. If they are equivalent, you do not. If the residual deviance is smaller, it depends on how many parameter you used whether you will conclude that the model explains significant parts of the data (see model comparison later).

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

Model comparison

m0 = glm(response~1           ,data=d,family=binomial)
m1 = glm(response~1 + contrast,data=d,family=binomial)
anova(m0,m1,test='LRT')

## Analysis of Deviance Table
## 
## Model 1: response ~ 1
## Model 2: response ~ 1 + contrast
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1       149     205.78                          
## 2       148     103.39  1   102.39 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The predictor contrast is highly significant

Which is (in the case of one predictor) exactly the same as:

Null Deviance - Residual Deviance: \((LL(M_{1}) - LL(M_{0}))\)

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

Poisson Regression

Count-data has an average rate per time unit: \(\lambda\)

Matings of animals per year (Biology)
How many/much seizures/headaches/pain per week (Medicine)
How many spikes per 10ms bin (Neuroscience)
How many eve-movements per minute/trial (CogPsy)

In the Logistic regression part we went through many important concepts that generalize extemely well to the whole family of GLMs. Nevertheless, logistic regression is special because it is used most often. Mastering the concepts of logistic regression will allow you to master the other GLMs in no time!

Poisson regression is probably the third most used regression from GLM family (after normal linear regression and logistic). Whenever you can count something (and thus get positive integers) you can apply poisson regression. Fun fact: if you only observe 0 and 1s, poisson regression falls back to logistic regression, if you observe a high number of events in all times (mean > 30), it can be approximated easily to linear regression. Neat!

The histogram I show on this slides shows the prototypical outcome distribution of a poisson process. Note that there are only integer. That is, there are no half fixations in this example. But of course the mean of this distribution (the rate \(\lambda\) can be any positive real number).

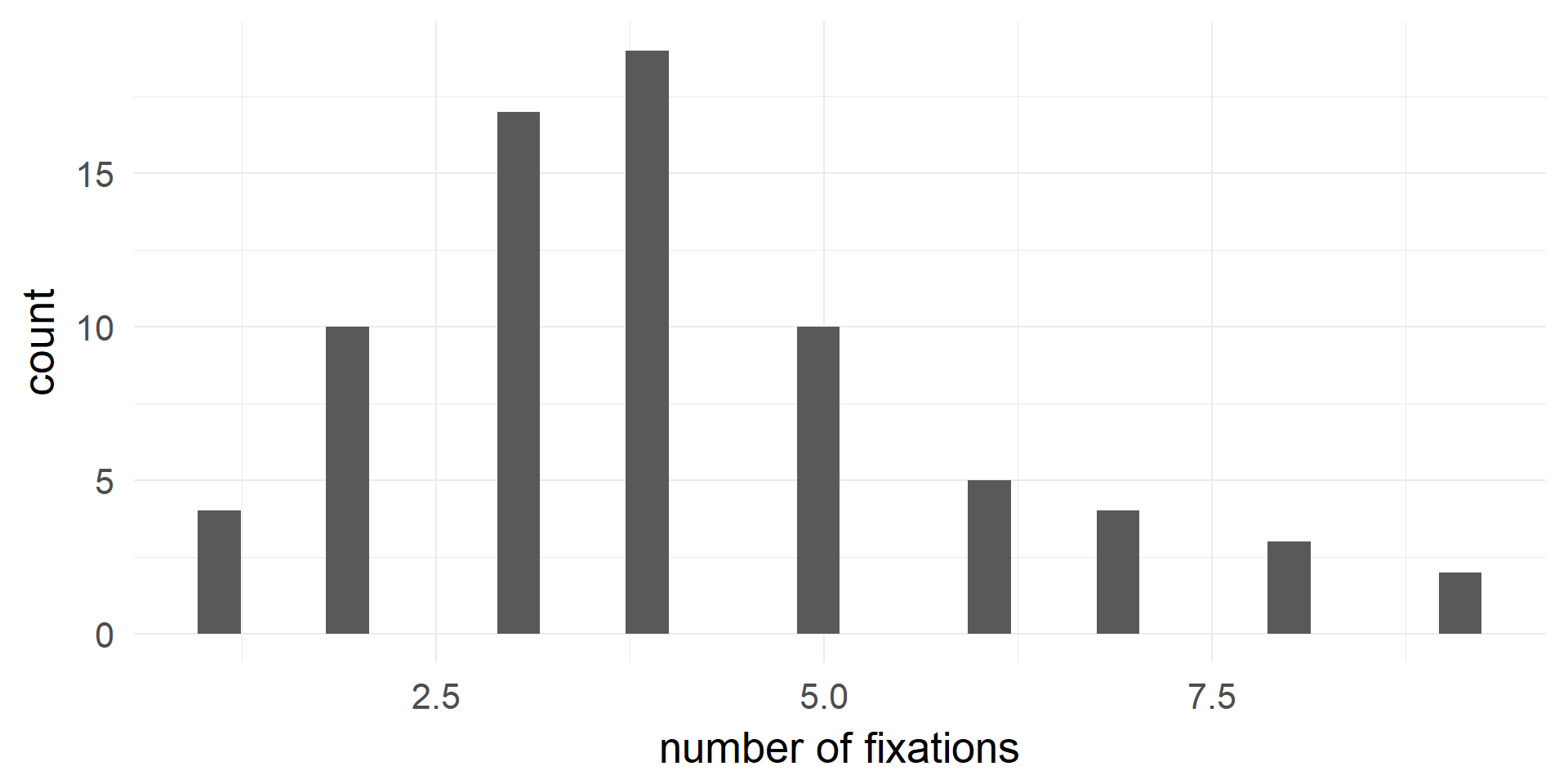
(fictional) Example: Poisson Regression

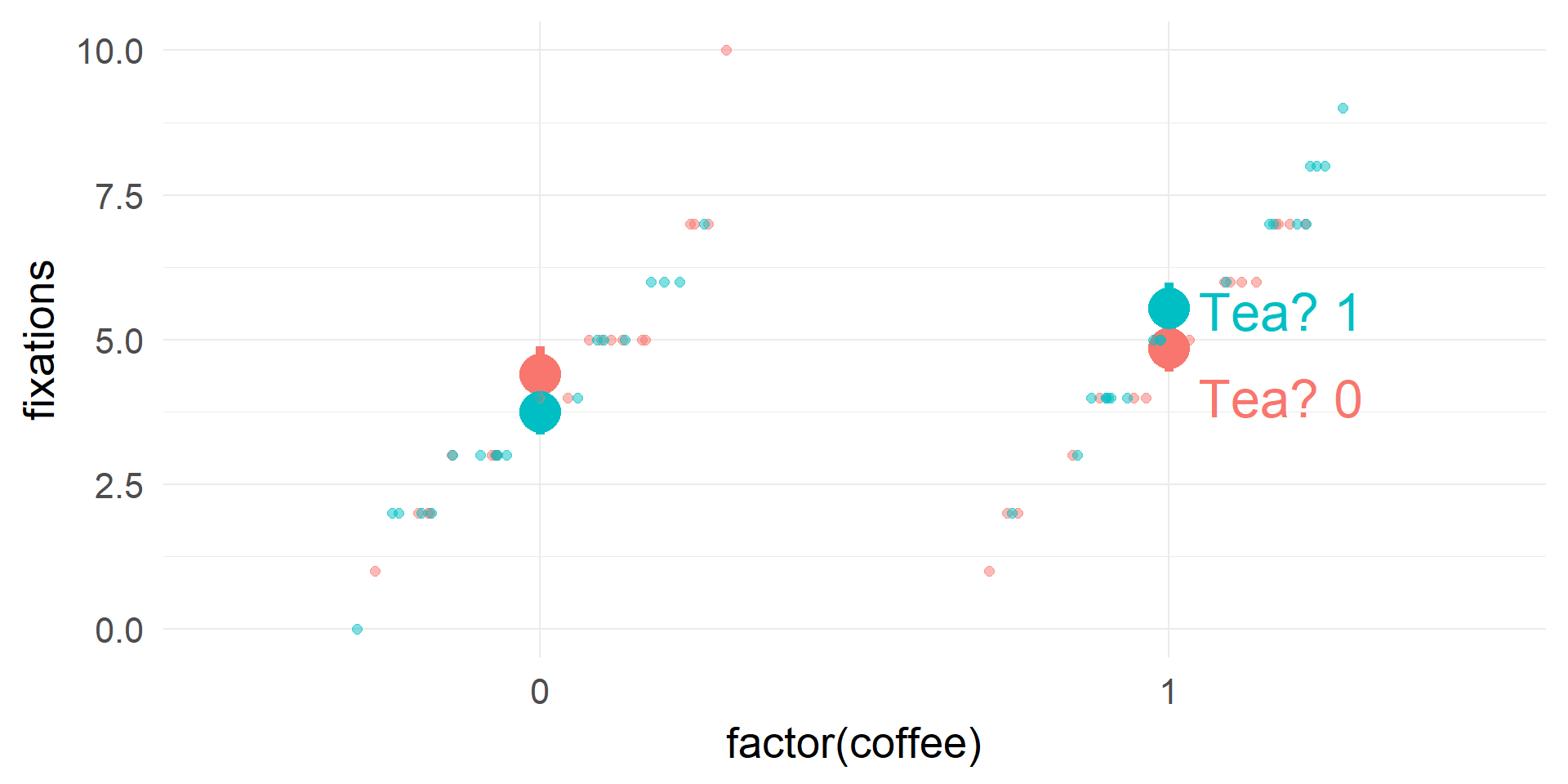
fitting in R and Interpretation

m1 = glm(data=df.pois,formula = fixations~coffee*tea,family=poisson)
summary(m1)

## 
## Call:
## glm(formula = fixations ~ coffee * tea, family = poisson, data = df.pois)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.73861  -0.69280   0.06776   0.59125   2.28465  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  1.48160    0.10660  13.899   <2e-16 ***
## coffee       0.09737    0.14722   0.661    0.508    
## tea         -0.15985    0.15715  -1.017    0.309    
## coffee:tea   0.29467    0.20980   1.405    0.160    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 75.082  on 79  degrees of freedom
## Residual deviance: 67.630  on 76  degrees of freedom
## AIC: 338.54
## 
## Number of Fisher Scoring iterations: 4

link-function g = \(log(\lambda) = X\beta\)

\(\lambda = e^{X\beta }\)

remember \(e^{a+b} = e^ae^b\) => Poisson parameters are multiplicative!

Interpretation of coefficients

	(Intercept)	coffee	tea	coffee:tea
coef(m1)	1.48	0.1	-0.16	0.29
exp(coef(m1))	4.40	1.1	0.85	1.34

Condition	\(log(\\lambda) = \\sum coef\)	\(\\lambda = \\prod e^{coef} = e^{\\sum coef}\)	\(\\lambda\)
Tea = 0 & Coffee = 0	1.48	4.4	4.4
Tea = 1 & Coffee = 0	1.48-0.16	4.4*0.85	3.74
Tea = 0 & Coffee = 1	1.48+0.09	4.4*1.1	4.84
Tea = 1 & Coffee = 1	1.48-0.16+0.09+0.29	4.4 * 0.85 * 1.1	5.51

anova(m1,test = 'LRT')

## Analysis of Deviance Table
## 
## Model: poisson, link: log
## 
## Response: fixations
## 
## Terms added sequentially (first to last)
## 
## 
##            Df Deviance Resid. Df Resid. Dev Pr(>Chi)  
## NULL                          79     75.082           
## coffee      1   5.4717        78     69.611  0.01933 *
## tea         1   0.0027        77     69.608  0.95859  
## coffee:tea  1   1.9782        76     67.630  0.15958  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

link-function g = \(log(\lambda)\)

As you can see, coffee seems to have a significant effect on the number of fixations (p<0.002). Tea does not. There is also no interaction. The model comparison works exactly the same way as with logistic regression. The program calculates the ratio of likelihoods (the difference of loglikelihoods) between a model with the parameter removed, and the one wit the parameter to be tested. It then looks up the difference in a \(\chi^2\) distribution, punishing for the number of additional parameters (because a model with n+1 parameters always fits better than a model with n parameters).

Why is the likelihoodratio-test different to the wald-test? They test different things and are only assymptotically (=> usually lots of data) equivalent. Its generally understood that the likelihoodratio-test gives better results. more information here

Note that type I/III/IV ANOVA does not matter here, because all factors are balanced

Overview

Binary Outcomes
- Example
- Logistic regression
- Units, odds, relative risks
- Interpretation of coefficients
- Checking the model
- Inference
Poisson Regression
GLMs
- Assumptions

The GLM family

Probability Distribution	Link-Function (g)	Statistical name
Normal	\(\beta X = y\)	Linear Regression
Bernoulli	\(\beta X = log(\frac {p} {1-p})\)	Logistic Regression
Poisson	\(\beta X = log(\lambda)\)	Poisson Regression
ExponentialGamma	\(\beta X = \frac 1 x\)	Gamma Regression

Assumptions

all GLMs data points are independent
the variance follows the mean in a specific way:
- Binomial: \(\sigma^2 = \mu(1-\mu)\)
- Poisson: \(\sigma^2 = \mu\)
- Gamma: \(\sigma^2 = \mu^2\)
- Normal: \(\sigma^2 = 1\) (constant)

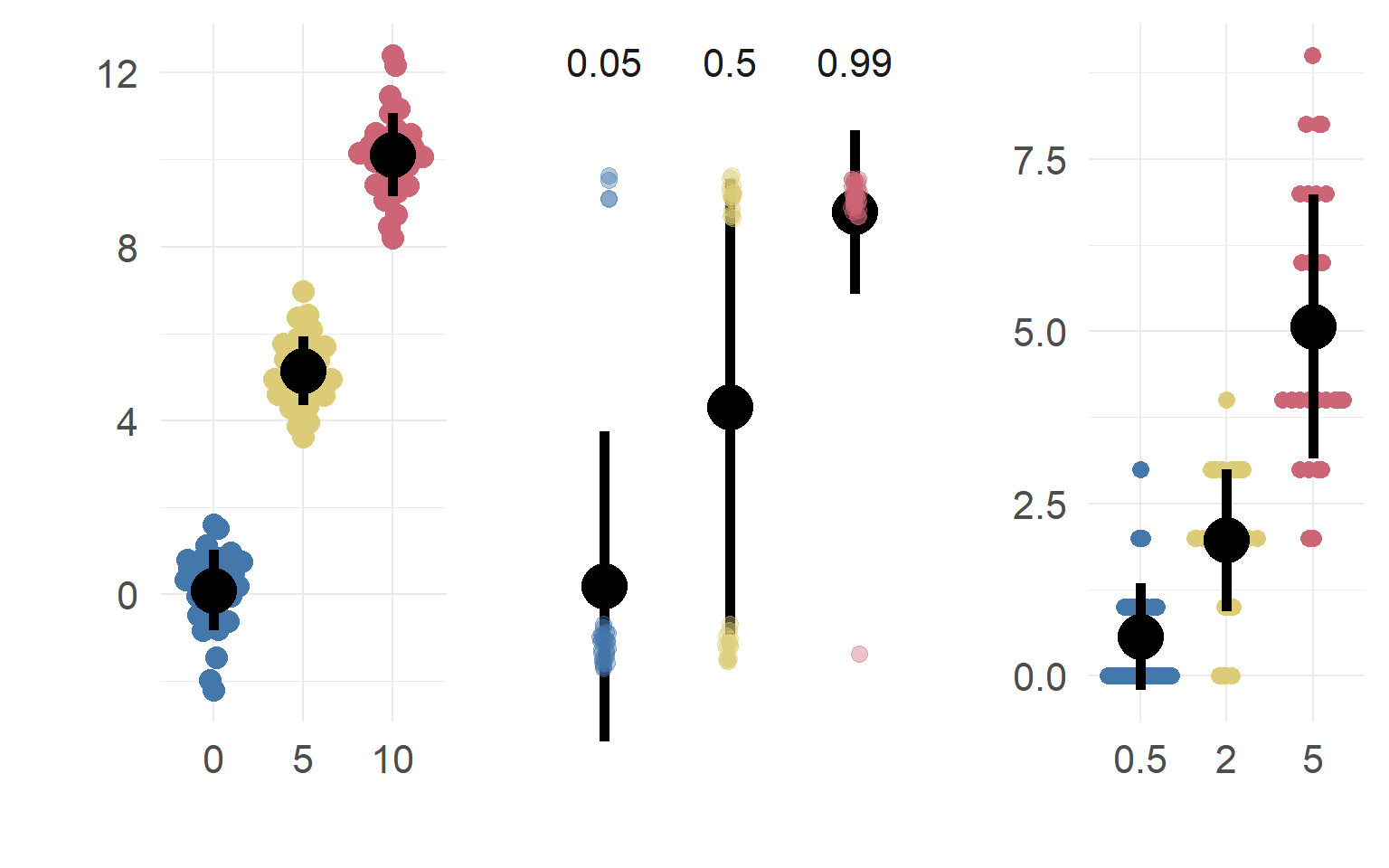
Poisson: A simple example when var != mean

dataSubset = df.pois$coffee==0 & df.pois$tea==0
mean(df.pois$fixations[dataSubset])

## [1] 4.4

var (df.pois$fixations[dataSubset])

## [1] 4.778947

mean(df.pois$fixations[dataSubset]*2)

## [1] 8.8

var (df.pois$fixations[dataSubset]*2)

## [1] 19.11579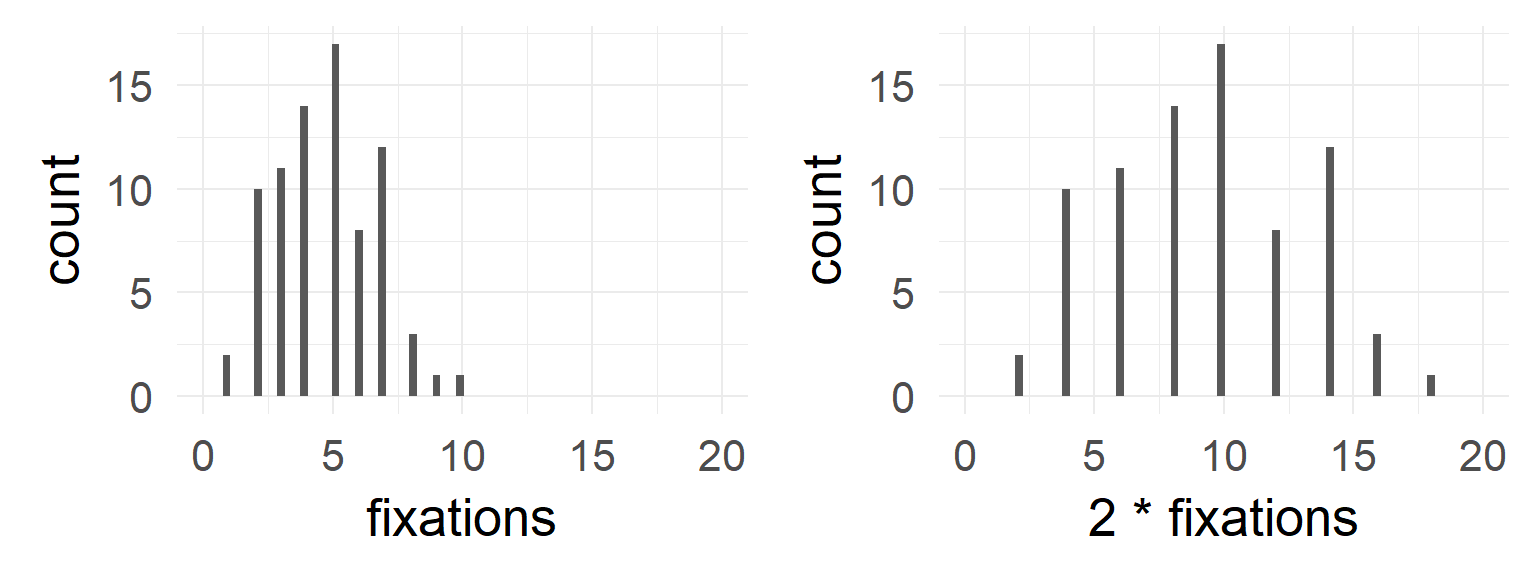

Binomial / Logistic regression

Impossible to have under/overdispersion with only an intercept

\(\sigma^2 = \mu(1-\mu)\)

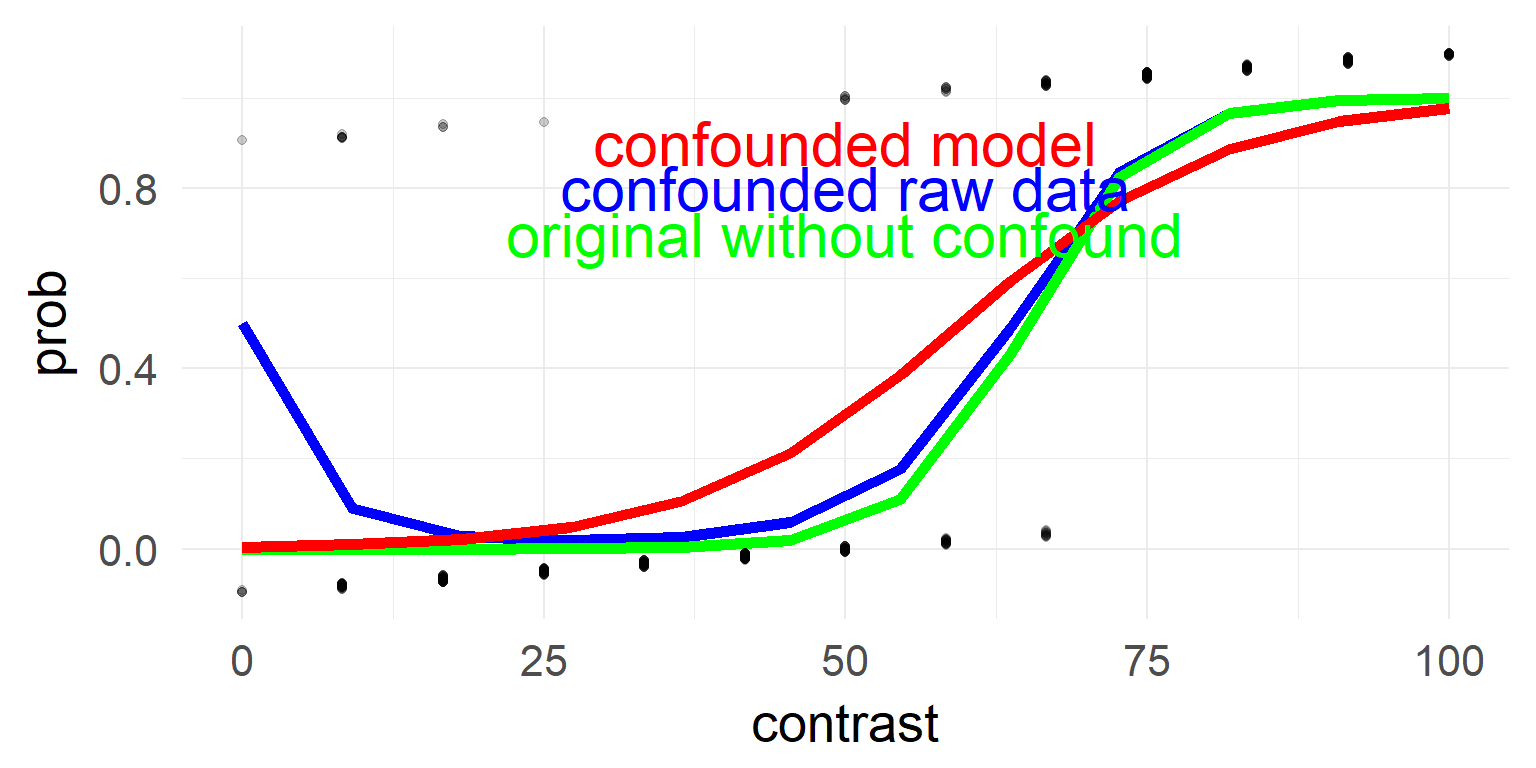
# Calculate dispersion parameter
sum(resid(mres, type = "pearson")^2) / df.residual(mres) # should be 1

## [1] 3.384014

deviance residual plot

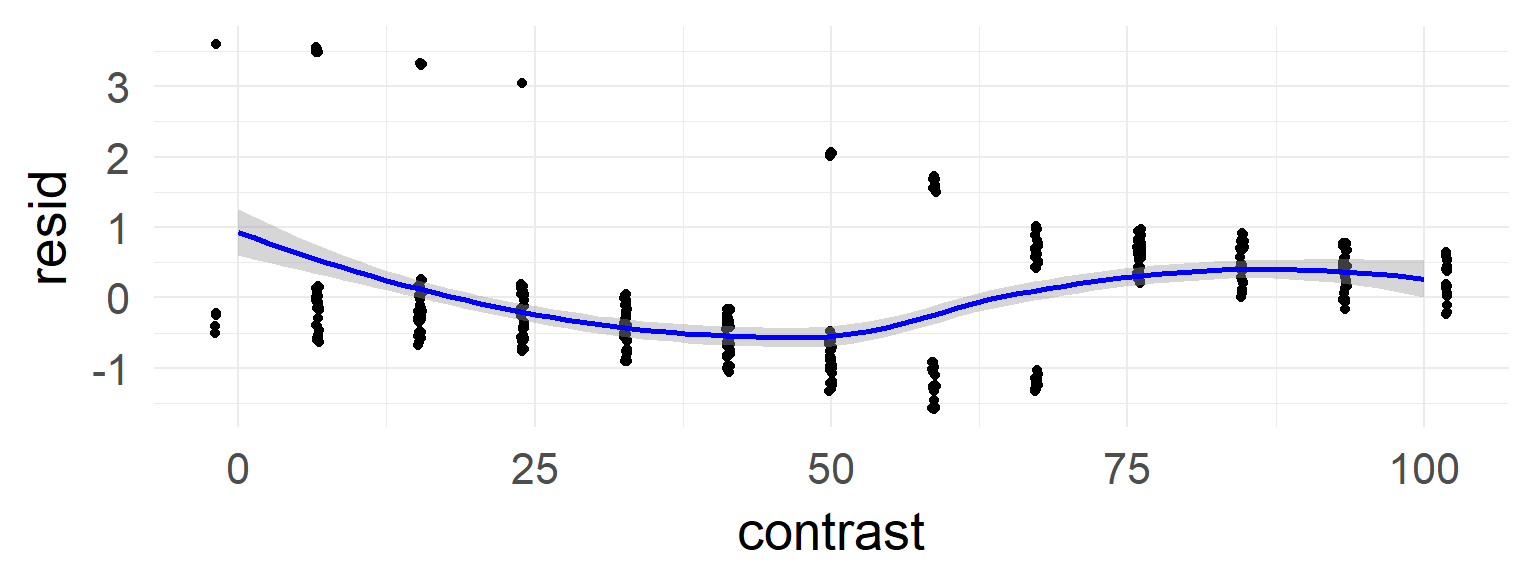
In the case of the confound a non-linearity can be seen.

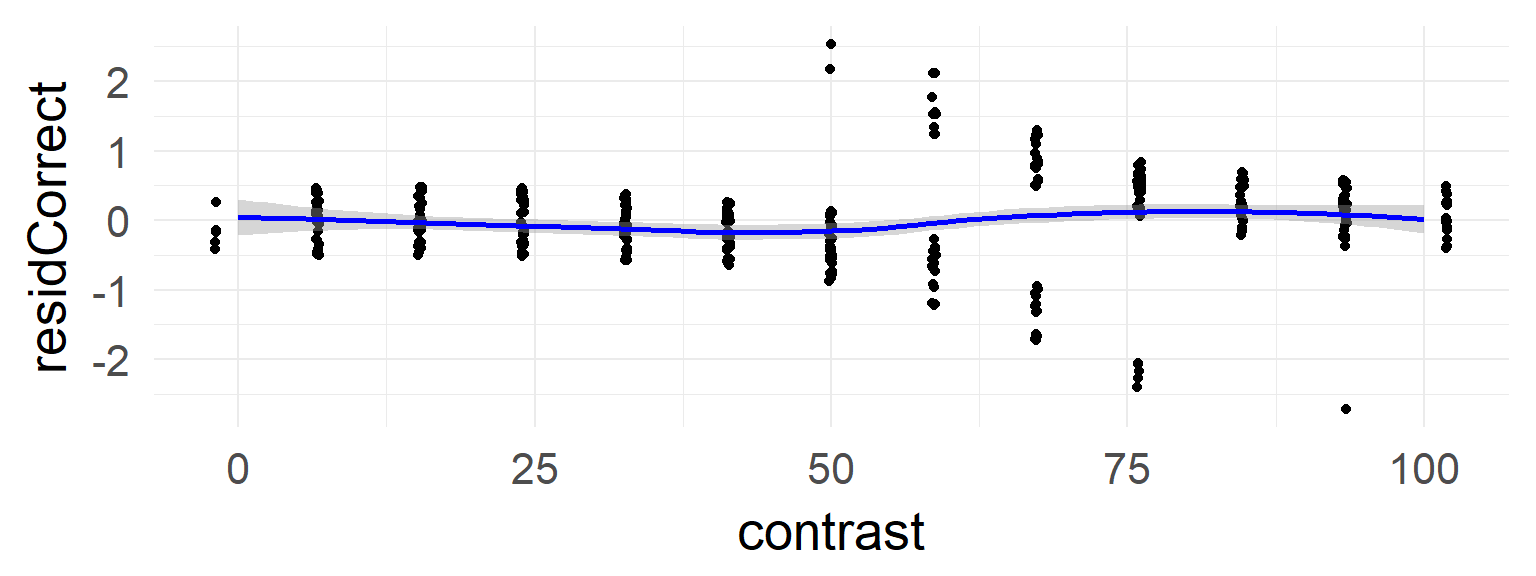
This is absent in the data without the confound

What to do?

Under/Overdispersion can occur in all GLMs (except normal)

Overdispersion comes mostly from:

Missing Factors
Non-linear effects
wrong link function
outliers

How to find out?

Check relation between variance and mean
logistic: Dispersion parameter read more
Poisson: mean / variance for binned data

How to compensate

Difficult in general
Quasibinomial / quasipoisson
Negative binomial read more)
Check out DHARMa (read more)

Excourse: Quasilikelihood example

Estimate an additional variance scaling factor. Thus (e.g. for Poisson):

\[Var = \phi \cdot mean\]

  mres1 = glm(data=d,response~ 1 + contrast,family=binomial)

## [1] "             Estimate Std. Error z value Pr(>|z|)    "   
## [2] "(Intercept) -5.514545   0.522216  -10.56   <2e-16 ***"   
## [3] "contrast     0.092564   0.008715   10.62   <2e-16 ***"   
## [4] "(Dispersion parameter for binomial family taken to be 1)"

sum(resid(mres1, type = "pearson")^2) / df.residual(mres1)

## [1] 3.384014

mres2 = glm(data=d,response~ 1 + contrast,family=quasibinomial)

## [1] "            Estimate Std. Error t value Pr(>|t|)    "                
## [2] "(Intercept) -5.51455    0.96065  -5.740 1.88e-08 ***"                
## [3] "contrast     0.09256    0.01603   5.774 1.56e-08 ***"                
## [4] "(Dispersion parameter for quasibinomial family taken to be 3.384015)"

Quasi-likelihoods make model comparisons more difficult

Summary

\(\hat y =\) g \((\beta X)\)

choose family (g) and link function

remember that estimated parameters are on a non-linear scale

use model comparison for statistics

check your assumptions

Generalised Linear Model

Benedikt Ehinger

March 21st, 2018

Slides & my Presentation style

What we want to be able to analyse

Overview

Example tasks with binomial data

Bernoulli vs Binomial

Bernoulli

Binomial

An example with a continuos variable

The Data

What is the probability to detect the target?

Let’s try linear regression

Truncating everything smaller 0 / larger 1:

A better fit

transforming y

logit & inv.logit

Overview

logistic regression

Running a logistic regression in R

the interplay of our two predictors

Overview

What are the units on the y-axis / the coefficients?

What are odds?

A closer look at the logit function

Background: Differences in probabilities, relative risk vs risk difference

The problem with relative risks

Overview

The constant / Intercept

In our example

Interpreting the slope

What are odds-ratios?

Back to the example

Coming back to relative risks

Intermediate Summary

Overview

Residuals

Excourse Likelihood function

Deviance / Residuals

Null & Residual Deviance

Overview

Model comparison

Overview

Poisson Regression

(fictional) Example: Poisson Regression

fitting in R and Interpretation

Interpretation of coefficients

Overview

The GLM family

Assumptions

Poisson: A simple example when var != mean

Binomial / Logistic regression

deviance residual plot

What to do?

Overdispersion comes mostly from:

How to find out?

How to compensate

Excourse: Quasilikelihood example

Summary

\(\hat y =\) g \((\beta X)\) choose family (g) and link function remember that estimated parameters are on a non-linear scale use model comparison for statistics check your assumptions

\(\hat y =\) g \((\beta X)\)

choose family (g) and link function

remember that estimated parameters are on a non-linear scale

use model comparison for statistics

check your assumptions